Tag Archives: statistics
Linear Regression vs Correlation: Examples
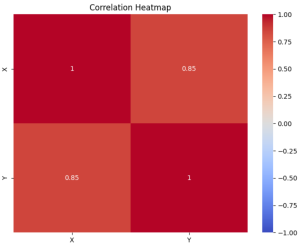
Linear regression and correlation are fundamental concepts in statistics, often used in data analysis to understand the relationship between two variables. Linear regression and correlation, while related, are not the same. They serve different purposes and provide different types of information. In this blog, we will explore each concept with examples to clarify their differences and applications. Linear Regression vs Correlation: Definition Linear Regression is a statistical method used for modeling the relationship between a dependent variable and one or more independent variables. The core idea is to find a linear equation that best describes this relationship, enabling the prediction of the dependent variable based on the values of the …
Chebyshev’s Theorem: Formula & Examples
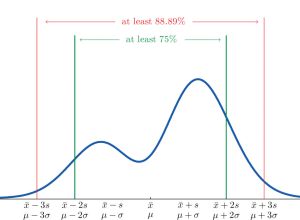
Chebyshev’s theorem is a fundamental concept in statistics that allows us to determine the probability of data values falling within a certain range defined by mean and standard deviation. This theorem makes it possible to calculate the probability of a given dataset being within K standard deviations away from the mean. It is important for data scientists, statisticians, and analysts to understand this theorem as it can be used to assess the spread of data points around a mean value. What is Chebyshev’s Theorem? Chebyshev’s Theorem, also known as Chebyshev’s Rule, states that in any probability distribution, the proportion of outcomes that lie within k standard deviations from the mean …
Standard Deviation vs Standard Error: Formula, Examples
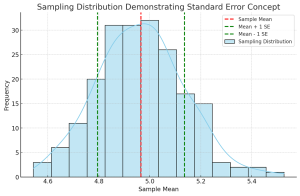
Understanding the differences between standard deviation and standard error is crucial for anyone involved in statistical analysis or research. These concepts, while related, serve different purposes in the realm of statistics. In this blog, we will delve into their differences, applications in research, formulas, and practical examples. Introduction to Standard Deviation & Standard Error At the heart of statistical analysis lies the need to understand and quantify variability. This is where standard deviation and standard error come into play. What’s standard deviation? Standard Deviation is a measure that reflects the amount of variation or dispersion within a dataset. It indicates how much individual data points deviate from the mean (average) …
Coefficient of Variation vs Standard Deviation

Last updated: 28th Nov, 2023 Understanding the difference between coefficient of variation (CV) and standard deviation (SD) is essential for statisticians and data scientists. While both concepts measure variability in a dataset, they are calculated differently and can be used in different scenarios for better understanding. Here, we will explore the coefficient of variation vs standard deviation differences to gain a better understanding of how to use them. Coefficient of Variation vs Standard Deviation Coefficient of Variation (CV) is a measure that is used to compare the amount of variation in a dataset relative to its mean value. It is calculated by taking the standard deviation divided by the mean, then …
Z-test vs T-test vs Chi-square test: Differences, Examples
In the world of data science, understanding the differences between various statistical tests is crucial for accurate data analysis. Three most popular tests – the Z-test, T-test, and Chi-square test – each serve specific purposes. This blog post will delve into their definitions, types, formulas, appropriate usage scenarios, and the Python/R packages that can be used for their implementation, along with real-world examples. Check out a detailed post on the differences between Z-test vs T-test. Definition: What’s Z-test vs T-test vs Chi-square test? The following represents the definition of each of the tests along with a real-world example: Z-test: The Z-test is a statistical test used to determine if there …
Different Types of Statistical Tests: Concepts

Last updated: 18th Nov, 2023 Statistical tests are an important part of data analysis. They help us understand the data and make inferences about the population. They are used to examine relationships between variables based on hypothesis testing. They are a way of analyzing data to see if there is a significant difference between the two groups or a group and population. In statistics, there are two main types of tests: parametric and non-parametric. Both types of tests are used to make inferences about a population based on a sample. The difference between the two types of tests lies in the assumptions that they make about the data. Parametric tests …
Types & Uses of Moments in Statistics
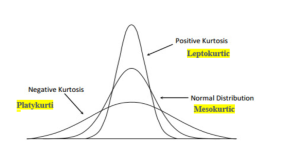
Last updated: 18th Nov, 2023 In statistics, moments are measures of the shape and variability of a data set. They are used to describe the location and dispersion of the data. There are several types of moments that can be calculated, each providing different information about the data set. Let’s take a look at some of these moments, its definitions, formula and examples highlighting how they can be used in statistical analysis. What are Moments in Statistics and what are their types? In statistics, moments are an important tool used to measure the characteristics of a distribution. Moments can provide useful information about the spread, shape, and center of a …
Two samples Z-test for Means: Formula & Examples
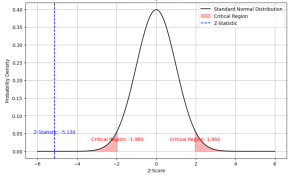
Last updated: 21st Nov, 2023 Statistical hypothesis testing is an essential tool in inferential statistics that enables researchers to make informed decisions about the population parameters based on sample statistics. One common hypothesis test for comparing two sample means is the Two-Sample Z-Test. In statistics, a two-sample z-test for means is used to determine if the means of two populations are equal. This test is used when the population standard deviations are known. As data scientists, it is of utmost importance to be able to understand and conduct this test accurately. In this blog, we will delve deeper into the Two-Sample Z-Test for means, exploring its formula, assumptions, and examples …
Histogram Plots using Matplotlib & Pandas: Python
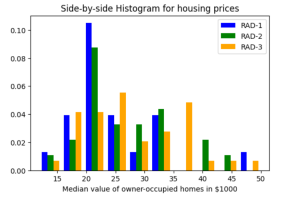
Executing the above code will print the following Histogram. Plotting multiple Histograms Side-by-Side using Matplotlib & Pandas When you want to understand the distribution of data with respect to different characteristics, you could plot the side-by-side or multiple histograms on the same plot. For example, when you want to understand the distribution of housing prices with respect to different values of accessibility to radial highways, you would want to print the histograms side-by-side on the same plot. Here is the code representing the printing of histogram plots side-by-side on the same plot: Here is how the side-by-side histogram plot would look like: Creating Stacked Histogram Plots using Matplotlib & Pandas …
Maximum Likelihood Estimation: Concepts, Examples
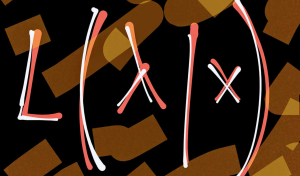
Maximum Likelihood Estimation (MLE) is a fundamental statistical method for estimating the parameters of a statistical model that make the observed data most probable. MLE is grounded in probability theory, providing a strong theoretical basis for parameter estimation. This is becoming more so important to learn fundamentals of MLE concepts as it is at the core of generative modeling (generative AI). Many models used in machine learning and statistics are based on MLE, including logistic regression, survival models, and various types of machine learning algorithms. MLE is particularly important for data scientists because it underpins many of the probabilistic machine learning models that are used today. These models, which are …
Wilcoxon Signed Rank Test: Concepts, Examples
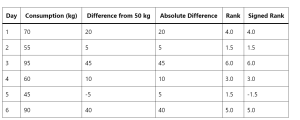
How can data scientists accurately analyze data when faced with non-normal distributions or small sample sizes? This is a challenge that often arises in the dynamic field of data science, where making precise inferences is crucial. Enter the Wilcoxon Signed Rank Test—a non-parametric statistical method that stands as a powerful alternative to the traditional t-test. This blog post aims to unravel the concepts and practical applications of the Wilcoxon Signed Rank Test, offering key insights for data scientists and researchers navigating complex data landscapes. The beauty of the Wilcoxon Signed Rank Test lies in its wide applicability across numerous fields. From healthcare, where it can compare the efficacy of different …
Minimum Description Length (MDL): Formula, Examples
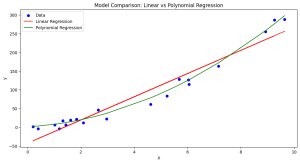
Learning the concepts of Minimum Description Length (MDL) is valuable for several reasons, especially for those involved in statistics, machine learning, data science, and related fields. One of the fundamental problems in statistics and data analysis is choosing the best model from a set of potential models. The challenge is to find a model that captures the essential features of the data without overfitting. This is where methods such as MDL, AIC, BIC, etc. comes to rescue. MDL offers a principled way to balance model complexity against the goodness of fit. This is crucial in many areas, such as machine learning and statistical modeling, where overfitting is a common problem. …
Pearson vs Spearman: Choosing the Right Correlation Coefficient
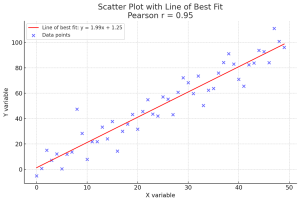
Are you as a data scientist trying to decipher relationship between two or more variables within vast datasets to solve real-world problems? Whether it’s understanding the connection between physical exercise and heart health, or the link between study habits and exam scores, uncovering these relationships is crucial. But with different methods at our disposal, how do we choose the most suitable one? This is where the concept of correlation comes into play, and particularly, the choice between Pearson and Spearman correlation coefficients becomes pivotal. The Pearson correlation coefficient is the go-to metric when both variables under consideration follow a normal distribution, assuming there’s a linear relationship between them. Conversely, the …
Pearson Correlation Coefficient: Formula, Examples
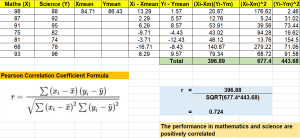
In the world of data science, understanding the relationship between variables is crucial for making informed decisions or building accurate machine learning models. Correlation is a fundamental statistical concept that measures the strength and direction of the relationship between two variables. However, without the right tools and knowledge, calculating correlation coefficients and p-values can be a daunting task for data scientists. This can lead to suboptimal decision-making, inaccurate predictions, and wasted time and resources. In this post, we will discuss what Pearson’s r represents, how it works mathematically (formula), its interpretation, statistical significance, and importance for making decisions in real-world applications such as business forecasting or medical diagnosis. We will …
t-distribution vs Normal distribution: Differences, Examples
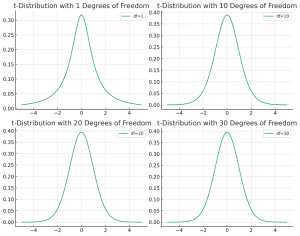
Understanding the differences between the t-distribution and the normal distribution is crucial for anyone delving into the world of statistics, whether they’re students, professionals in research, or data enthusiasts trying to make sense of the world through numbers. But why should one care about the distinction between these two statistical distributions? The answer lies in the heart of hypothesis testing, confidence interval estimation, and predictive modeling. When faced with a set of data, choosing the correct distribution to describe it can greatly influence the accuracy of your conclusions. The normal distribution is often the default assumption due to its simplicity and the central limit theorem, which states that the means …
Insurance & Linear Regression Model Example
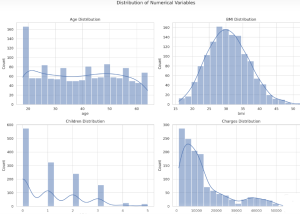
Ever wondered how insurance companies determine the premiums you pay for your health insurance? Predicting insurance premiums is more than just a numbers game—it’s a task that can impact millions of lives. In this blog, we’ll demystify this complex process by walking you through an end-to-end example of predicting health insurance premium charges by demonstrating with Python code example. Specifically, we’ll use a linear regression model to predict these charges based on various factors like age, BMI, and smoking status. Whether you’re a beginner in data science or a seasoned professional, this blog will offer valuable insights into building and evaluating regression models. What is Linear Regression? Linear Regression is …
I found it very helpful. However the differences are not too understandable for me