Linear regression and correlation are fundamental concepts in statistics, often used in data analysis to understand the relationship between two variables. Linear regression and correlation, while related, are not the same. They serve different purposes and provide different types of information. In this blog, we will explore each concept with examples to clarify their differences and applications.
Linear Regression vs Correlation: Definition
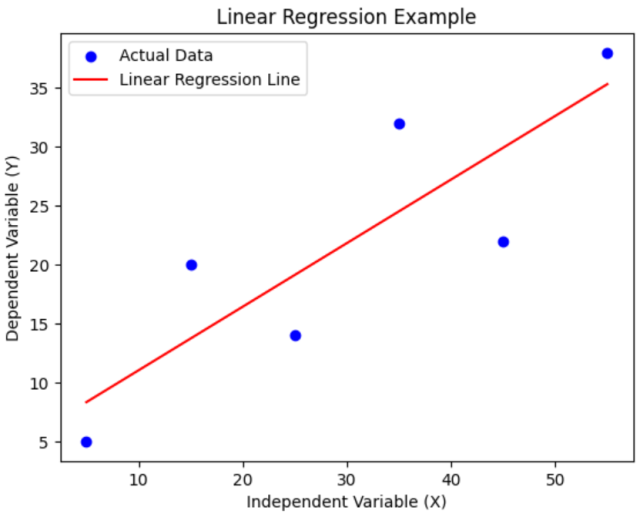
Linear Regression is a statistical method used for modeling the relationship between a dependent variable and one or more independent variables. The core idea is to find a linear equation that best describes this relationship, enabling the prediction of the dependent variable based on the values of the independent variables. The model that is used to make the prediction is called as linear regression model. The following is the example of linear regression model, the output of which is represented as linear regression line. Learn more about this concept from this page: Linear Regression Explained with Real-life Examples.
Correlation, in statistics, is a measure that indicates the extent to which two or more variables fluctuate together. It provides a single number, the correlation coefficient, which quantifies the strength and direction of a linear relationship between two variables. The most commonly used correlation coefficient is Pearson’s correlation coefficient, denoted as r, which ranges from -1 to +1. The value, r =1, is a perfect positive linear correlation, meaning as one variable increases, the other variable increases at a constant rate. The value, r = -1, is a perfect negative linear correlation, indicating that as one variable increases, the other decreases at a constant rate. The value, r = 0, represents no linear correlation; the variables do not have a linear relationship. Check out this blog – Pearson Correlation Coefficient: Formula, Examples. Another popular correlation coefficient is Spearman Correlation Coefficient.
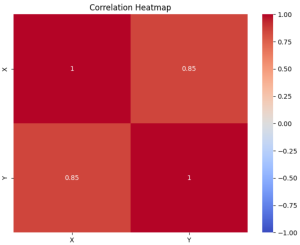
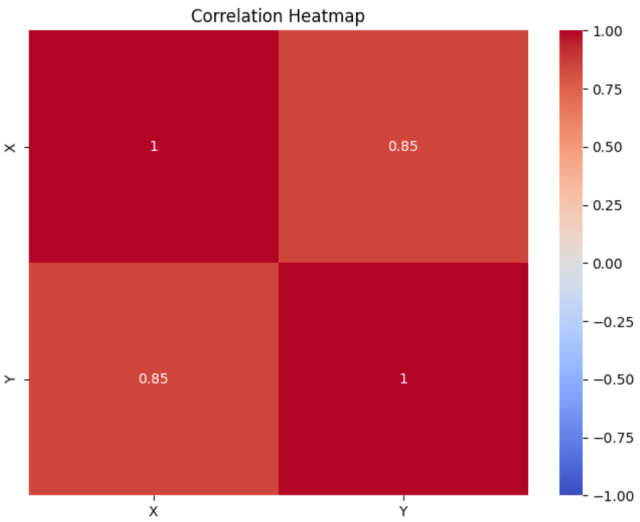
The following is correlation heatmap which is used to visualize the correlation matrix. The correlation matrix shows the correlation coefficients between each pair of variables. The heatmap is annotated with the correlation coefficients and uses a color scale to represent the strength of the correlation. The plot provides a visual representation of how strongly the variables are correlated, with 1 indicating a perfect positive correlation, -1 indicating a perfect negative correlation, and 0 indicating no correlation.
Linear Regression vs Correlation: Similarities
The following are some of the key similarities between correlation and linear regression:
- Relationship Analysis: Both correlation and linear regression analyze the relationship between two variables.
- Quantitative Data: They are typically applied to quantitative, or numerical, data.
- Graphical Representation: The relationship between the two variables in both cases can often be visualized using a scatter plot.
Correlation vs Linear Regression: Differences
The following are some of the key differences between linear regression and correlation:
- Purpose and Output:
- Linear Regression: Used to predict the value of a dependent variable based on the value of at least one independent variable. It provides an equation (Y = aX + b) for prediction.
- Correlation: Measures the strength and direction of the relationship between two variables. It does not provide an equation for prediction, but a correlation coefficient (ranging from -1 to 1).
- Direction:
- Linear Regression: Directional. It assumes a cause-and-effect relationship where one variable (independent) influences the other (dependent).
- Correlation: Non-directional. It only indicates how closely two variables are related without implying causation.
Correlation vs Linear Regression: When to use?
Choosing between linear regression and correlation depends on your analysis goals:
Use Linear Regression When:
- Predicting or Estimating Values: To predict one variable based on another (e.g., house prices based on size).
- Understanding Relationship Nature: To analyze how changes in one variable affect another (e.g., the effect of education on salary).
- Quantifying Variable Impact: To measure the impact of one variable on another (e.g., advertising spend on sales revenue).
- Causal Inference (Cautiously): For potential causal relationships, though careful consideration and additional methods are often needed.
Use Correlation When:
- Measuring Relationship Strength: To find out how strongly two variables are related (e.g., study time and exam scores).
- Preliminary Analysis: For initial exploration of relationships between variables.
- Analyzing Non-Causal Relationships: To identify relationships without inferring causality (e.g., age and fitness level).
- Assessing Multiple Variables: For examining relationships among multiple variables simultaneously (e.g., correlations between different stock prices).
Linear Regression and Correlation Example
You are a real estate analyst looking to understand the dynamics of the housing market in a particular city. You have a dataset containing information about recently sold properties, including their sale prices, square footage, location, age, and proximity to key amenities like schools, parks, and transportation.
Using Linear Regression
Objective: Predicting House Prices
- Independent Variables: Square footage, age of the property, distance from city center, proximity to schools, etc.
- Dependent Variable: Sale price of the houses.
You would use linear regression to develop a model that predicts the sale price of a house based on these factors. By analyzing the coefficients of the regression model, you can understand how each factor, like square footage or age, impacts the sale price. For instance, the model could reveal how much the price increases for each additional square foot of space.
Using Correlation
Objective: Understanding Relationships Between Features
- Variables: Same as above (square footage, age, distance from city center, etc.), including the sale price.
Here, you would calculate correlation coefficients between different pairs of variables to understand their relationships. For example, you might find a strong positive correlation between square footage and sale price, indicating that larger homes tend to sell for higher prices. Similarly, you might explore the correlation between the age of the property and its sale price to see if newer properties tend to be more expensive.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me