Eigenvalues and eigenvectors are important concepts in linear algebra that have numerous applications in data science. They provide a way to analyze the structure of linear transformations and matrices, and are used extensively in many areas of machine learning, including feature extraction, dimensionality reduction, and clustering.
In simple terms, eigenvalues and eigenvectors are the building blocks of linear transformations. Eigenvalues represent the scaling factor by which a vector is transformed when a linear transformation is applied, while eigenvectors represent the directions in which the transformation occurs.
In this post, you will learn about why and when you need to use Eigenvalues and Eigenvectors? As a data scientist/machine learning Engineer, one must need to have a good understanding of concepts related to Eigenvalues and Eigenvectors as these concepts are used in one of the most popular dimensionality reduction techniques – Principal Component Analysis (PCA). In PCA, these concepts help in reducing the dimensionality of the data (curse of dimensionality) resulting in a simpler model which is computationally efficient and provides greater generalization accuracy. In this post, the following topics will be covered:
Background – Why use Eigenvalues & Eigenvectors?
Before getting a little technical, let’s understand why we need Eigenvalues and Eigenvectors, in layman’s terms.
In order to understand a thing or problem in a better manner, we tend to break down things into smaller components and understand the things’ properties by understanding these smaller components. When we break down things into their most elementary components or basic elements, we can get a great understanding of the things. For example, if we want to understand a wooden table, we can understand it in a better manner by understanding the basic elements, wood, of which it is made. We can then understand the properties of wooden tables in a better manner.
Let’s take another example of an integer 18. In order to understand the integer, we can break down or decompose the integer into its prime factors such as 2 x 3 x 3. We get to know the properties of the integer 18 such as the following:
- Any multiple of 18 is divisible by 3.
- 18 is not divisible by 5 or 7
Similarly, Matrices can be broken down or decomposed in ways that can show information about their functional properties that are not obvious from the representation of the matrix as an array of elements. One of the most widely used kinds of matrix decomposition is called eigen-decomposition, in which we decompose a matrix into a set of eigenvectors and eigenvalues. You may want to check out this page from Deeplearning book by Ian Goodfellow, Yoshua Bengio, and Aaron C. By the way, this reasoning technique of breaking down things and arriving at the most basic elements of which thing is made to understand and innovate is also called first principles thinking.
In simple words, the concept of Eigenvectors and Eigenvalues are used to determine a set of important variables (in form of a vector) along with scale along different dimensions (key dimensions based on variance) for analyzing the data in a better manner. Let’s take a look at the following picture:
When you look at the above picture (data) and identify it as a tiger, what are some of the key information (dimensions / principal components) you use to call it out like a tiger? Is it not the face, body, legs, etc information? These principal components/dimensions can be seen as eigenvectors with each one of them having its own elements. For example, the body will have elements such as color, built, shape, etc. The face will have elements such as nose, eyes, color, etc. The overall data (image) can be seen as a transformation matrix. The data (transformation matrix) when acted on the eigenvectors (principal components) will result in the eigenvectors multiplied by the scale factor (eigenvalue). And, accordingly, you can identify the image as the tiger.
The solution to real-world problems often depends upon processing a large volume of data representing different variables or dimensions. For example, take the problem of predicting the stock prices. This is a machine learning / predictive analytics problem. Here the dependent value is stock price and there are a large number of independent variables on which the stock price depends. Using a large number of independent variables (also called features), training one or more machine learning models for predicting the stock price will be computationally intensive. Such models turn out to be complex models.
Can we use the information stored in these variables and extract a smaller set of variables (features) to train the models and do the prediction while ensuring that most of the information contained in the original variables is retained/maintained. This will result in simpler and computationally efficient models. This is where eigenvalues and eigenvectors come into the picture.
Feature extraction algorithms such as Principal component analysis (PCA) depend on the concepts of Eigenvalues and Eigenvectors to reduce the dimensionality of data (features) or compress the data (data compression) in form of principal components while retaining most of the original information. In PCA, the eigenvalues and eigenvectors of the features covariance matrix are found and further processed to determine top k eigenvectors based on the corresponding eigenvalues. Thereafter, the projection matrix is created from these eigenvectors which are further used to transform the original features into another feature subspace. With a smaller set of features, one or more computationally efficient models can be trained with reduced generalization error. Thus, it can be said that Eigenvalues and Eigenvectors concepts are key to training computationally efficient and high-performing machine learning models. Data scientists must understand these concepts very well.
Finding Eigenvalues and Eigenvectors of a matrix can be useful for solving problems in several fields such as some of the following wherever there is a need for transforming a large volume of multi-dimensional data into another subspace comprising of smaller dimensions while retaining most information stored in the original data. The primary goal is to achieve optimal computational efficiency.
- Machine learning (dimensionality reduction / PCA, facial recognition)
- Designing communication systems
- Designing bridges (vibration analysis, stability analysis)
- Quantum computing
- Electrical & mechanical engineering
- Determining oil reserves by oil companies
- Construction design
- Stability of the system
What are Eigenvalues & Eigenvectors?
Eigenvectors are the vectors that when multiplied by a matrix (linear combination or transformation) result in another vector having the same direction but scaled (hence scaler multiple) in forward or reverse direction by a magnitude of the scaler multiple which can be termed as Eigenvalue. In simpler words, the eigenvalues are scalar values that represent the scaling factor by which a vector is transformed when a linear transformation is applied. In other words, eigenvalues are the values that scale eigenvectors when a linear transformation is applied.
Here is the formula for what is called eigenequation.
[latex]
Ax = \lambda x
[/latex]
In the above equation, the matrix A acts on the vector x and the outcome is another vector Ax having the same direction as the original vector x but scaled/shrunk in forward or reverse direction by a magnitude of scaler multiple, [latex]\lambda[/latex]. The vector x is called an the eigenvector of A and [latex]\lambda[/latex] is called its eigenvalue. Let’s understand pictorially what happens when a matrix A acts on a vector x. Note that the new vector Ax has a different direction than vector x.
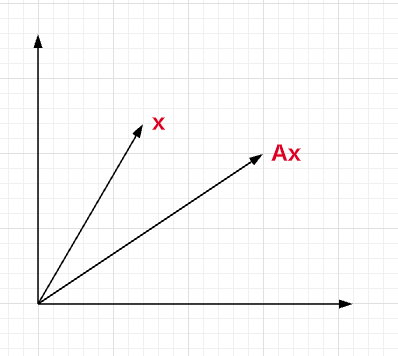
When the matrix multiplication with vector results in another vector in the same/opposite direction but scaled in forward / reverse direction by a magnitude of scaler multiple or eigenvalue ([latex]\lambda[/latex]), then the vector is called the eigenvector of that matrix. Here is the diagram representing the eigenvector x of matrix A because the vector Ax is in the same/opposite direction of x.
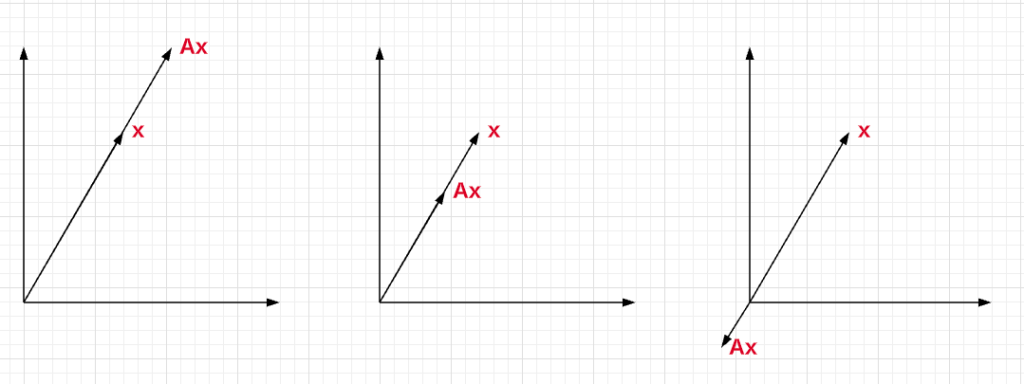
Here is further information on the value of eigenvalues:
There are several key properties of eigenvalues and eigenvectors that are important to understand. These include:
- Eigenvectors are non-zero vectors: Eigenvectors cannot be zero vectors, as this would imply that the transformation has no effect on the vector.
- Eigenvalues can be real or complex: Eigenvalues can be either real or complex numbers, depending on the matrix being analyzed.
- Eigenvectors can be scaled: Eigenvectors can be scaled by any non-zero scalar value and still be valid eigenvectors.
- Eigenvectors can be orthogonal: Eigenvectors that correspond to different eigenvalues are always orthogonal to each other.
Many disciplines traditionally represent vectors as matrices with a single column rather than as matrices with a single row. For that reason, the word “eigenvector” in the context of matrices almost always refers to a right eigenvector, namely a column vector.
How to Calculate Eigenvector & Eigenvalue?
Here are the steps to calculate the eigenvalue and eigenvector of any matrix A.
- Calculate one or more eigenvalues depending upon the number of dimensions of a square matrix
- Determine the corresponding eigenvectors
For calculating the eigenvalues, one needs to solve the following equation:
[latex]
Ax = \lambda x
\\Ax – \lambda x = 0
\\(A – \lambda I)x = 0
[/latex]
For non-zero eigenvector, the eigenvalues can be determined by solving the following equation:
[latex]
A – \lambda I = 0
[/latex]
In above equation, I is identity matrix and [latex]\lambda[/latex] is eigenvalue. Once eigenvalues are determined, eigenvectors are determined by solving the equation [latex](A – \lambda I)x = 0[/latex]
When to use Eigenvalues & Eigenvectors?
Eigenvectors and eigenvalues are powerful tools that can be used in a variety of ways in machine learning. Here are some of the scenarios / reasons when you can use eigenvalues and eignevectors:
- Feature extraction: Feature extraction is a process of identifying the most important features of a dataset that can be used to model and analyze the data. Eigenvalues and eigenvectors can be used to extract the most important features of a dataset by identifying the directions of maximum variation in the data. These directions can be represented by the eigenvectors, and the amount of variation in each direction can be represented by the corresponding eigenvalue. The most important features of the dataset can then be selected based on their corresponding eigenvalues.
- Principal component analysis (PCA): Principal component analysis (PCA) is a widely used technique for data dimensionality reduction that is based on the eigendecomposition of the covariance matrix of the data. PCA works by finding the eigenvectors and eigenvalues of the covariance matrix and using them to project the data onto a lower-dimensional space. The resulting projected data can then be used for further analysis, such as clustering or classification.
- Spectral Clustering: Clustering is a process of grouping similar data points together based on some similarity metric. One kind of clustering known as spectral clustering makes use of the concept of Eigenvalues and Eigenvectors. Spectral clustering is a graph-based clustering method that uses the eigenvalues and eigenvectors of the similarity matrix of the data points to partition the data into clusters. The algorithm works by first constructing a similarity matrix, where the element (i, j) of the matrix represents the similarity between data points i and j. The eigendecomposition of the similarity matrix is then performed to obtain the eigenvectors and eigenvalues of the matrix. The eigenvectors are then used to transform the data into a lower-dimensional space, where clustering is performed using a simple algorithm like K-means clustering.
References
- What are Eigenvalues and Eigenvectors?
- Introduction to Principal Component Analysis (PCA)
- Points of Significance – PCA
- A tutorial on Principal Component Analysis – Lindsay Smith
- Intuitive understanding of Eigenvectors – Key to PCA
- Applications of Eigenvalues & Eigenvectors
- Real-life examples of Eigenvalues & Eigenvectors
Conclusions
Here are some learnings from this post:
- An eigenvector is a vector that when multiplied with a transformation matrix results in another vector multiplied with a scaler multiple having the same direction as Eigenvector. This scaler multiple is known as Eigenvalue
- Eigenvectors and Eigenvalues are key concepts used in feature extraction techniques such as Principal Component Analysis which is an algorithm used to reduce dimensionality while training a machine learning model.
- Eigenvalues and Eigenvector concepts are used in several fields including machine learning, quantum computing, communication system design, construction designs, electrical and mechanical engineering, etc.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com
- Model Parallelism vs Data Parallelism: Examples - April 11, 2024
- Model Complexity & Overfitting in Machine Learning: How to Reduce - April 10, 2024
- 6 Game-Changing Features of ChatGPT’s Latest Upgrade - April 9, 2024
I’m an old guy with almost no math background. But in my reading, 90% nonfiction, I run across the words “eigenvalue” and “eigenvector.” Your post helped me understand these things.
A very good insight of Eigen values and Eigen Vector. You post is useful to many.
Thank you Krishna for the feedback.
I found your writing about eigenvector and eigenvalue is very helpful for my understanding!
Thank you
Thank you for the great explanation!
simple and great explaination
Very Nice Explaination. Thankyiu very much,