How can data scientists accurately analyze data when faced with non-normal distributions or small sample sizes? This is a challenge that often arises in the dynamic field of data science, where making precise inferences is crucial. Enter the Wilcoxon Signed Rank Test—a non-parametric statistical method that stands as a powerful alternative to the traditional t-test. This blog post aims to unravel the concepts and practical applications of the Wilcoxon Signed Rank Test, offering key insights for data scientists and researchers navigating complex data landscapes.
The beauty of the Wilcoxon Signed Rank Test lies in its wide applicability across numerous fields. From healthcare, where it can compare the efficacy of different treatments, to business, where it can assess the impact of a new marketing strategy, this test has the versatility to handle a diverse range of data types and scenarios. It’s particularly useful in before-and-after studies, matched-pair analyses, and instances requiring the comparison of related samples.
Whether you’re a seasoned data scientist or just starting out, this post will guide you through the intricacies of the Wilcoxon Signed Rank Test, demonstrating its crucial role in data analysis and decision-making.
What’s Wilcoxon Signed Rank Test?
The Wilcoxon Signed Rank Test is a non-parametric statistical test used to compare two related samples, matched samples, or repeated measurements on a single sample to assess whether their population mean ranks differ. It’s an alternative to the paired Student’s t-test when the data cannot be assumed to be normally distributed.
How does Wilcoxon signed rank test work?
The following is how Wilcoxon signed rank test works:
- Hypothesis formulation:
- Null Hypothesis (H0): The median difference between the paired samples is zero.
- Alternative Hypothesis (H1): The median difference is not zero.
- Perform Hypothesis Testing:
- Differences: Compute the differences between pairs of observations (e.g., before and after treatment).
- Ranks: Assign ranks to these differences, ignoring the sign (absolute value).
- Signs: Attach the signs of the differences to their ranks.
- Sum of Ranks: Sum the ranks for the positive differences and the ranks for the negative differences.
- Test Statistic: The test statistic is the smaller of the two sums of ranks.
- Significance level: Determine level of significance which would be used for hypothesis testing.
- Evaluate whether to reject the null hypothesis or otherwise.
- Dealing with large vs small samples:
- Small Samples: In small samples, the distribution of the test statistic under the null hypothesis is calculated exactly.
- Large Samples: For large samples, the distribution can be approximated by a normal distribution, simplifying the calculation.
Types of Problems Wilcoxon Signed Rank Test Solve (When to use)
The following are unique problems which can be addressed using WIlcoxon signed rank test:
- Non-Normal Data Analysis:
- Allows for hypothesis testing when data are skewed, heavy-tailed, or otherwise non-normally distributed.
- Small Sample Sizes:
- Effective in situations where sample sizes are too small to reliably estimate the parameters of a normal distribution.
- Ordinal Data:
- Can be used with ordinal data (ranked data), not just interval or ratio measurements.
Wilcoxon Signed Rank Test Example
Let’s take a look at a real world problem and understand how Wilcoxon signed rank test helps in making the decision.
Suppose that you are managing a canteen for students of a hostel. In particular, your duty is to ensure that there is ample rice cooked on a daily basis. During the first week of your work, the students consumed 70, 55, 95, 60, 45 and 90 kg of rice.
Does this imply significant evidence, at the 5% level of significance, that the median daily consumption of rice is more than 50 kgs?
To determine if there’s significant evidence that the median daily consumption of rice is more than 50 kg, we can perform a one-sample Wilcoxon Signed Rank Test. This test is suitable for small sample sizes and doesn’t assume a normal distribution of the data. Let’s proceed with the following steps:
- Hypothesis formulation:
- Null Hypothesis (H0): The median daily consumption of rice is 50 kg.
- Alternative Hypothesis (H1): The median daily consumption of rice is more than 50 kg.
- Data gathering:
- Daily consumption for the first week: 70, 55, 95, 60, 45, and 90 kg.
- Perform hypothesis test:
- Calculate the differences from the hypothesized median (50 kg).
- Rank these differences.
- Perform a one-tailed Wilcoxon Signed Rank Test as we are testing if the median is greater than 50 kg.
- Significance Level:
- We’ll use a 5% significance level (α=0.05).
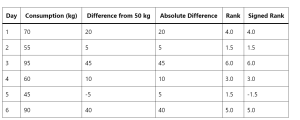
Here is the analysis of the rice consumption data presented in tabular format, using the Wilcoxon Signed Rank Test:
| Day | Consumption (kg) | Difference from 50 kg | Absolute Difference | Rank | Signed Rank |
|---|---|---|---|---|---|
| 1 | 70 | 20 | 20 | 4.0 | 4.0 |
| 2 | 55 | 5 | 5 | 1.5 | 1.5 |
| 3 | 95 | 45 | 45 | 6.0 | 6.0 |
| 4 | 60 | 10 | 10 | 3.0 | 3.0 |
| 5 | 45 | -5 | 5 | 1.5 | -1.5 |
| 6 | 90 | 40 | 40 | 5.0 | 5.0 |
- Sum of Positive Ranks: 19.5
- Sum of Negative Ranks: -1.5
The following is the interpretation:
- The differences are calculated relative to the hypothesized median (50 kg).
- The absolute differences are ranked, with the original sign of the difference reapplied to determine the signed rank.
- In this analysis, the sum of the positive ranks (19.5) was used in the Wilcoxon test since we were testing if the median consumption is greater than 50 kg.
- The significant result (p-value ~ 0.046875) suggests that the median daily consumption of rice is significantly more than 50 kg based on this data.
Python Code Example for Wilcoxon Signed Rank Test
The following is the Python code using the wilcoxon method of Scipy.stats for solving the decision problem related to rice discussed in the earlier section.
The results are as follows:
- Wilcoxon Statistic: 19.5
- One-Tailed p-Value: Approximately 0.046875
The following is the interpretation of the result:
- The p-value of approximately 0.046875 is just below the 5% significance level (α=0.05).
- This suggests that there is significant evidence at the 5% level to reject the null hypothesis.
- Therefore, based on this data, we can conclude that the median daily consumption of rice is significantly more than 50 kgs.
This implies that in managing the canteen for the hostel, it would be advisable to prepare more than 50 kg of rice daily to meet the students’ needs.
Difference: Wilcoxon Signed Rank Test vs Sign Test
The Wilcoxon Signed Rank Test and the Sign Test are both non-parametric tests used to compare paired or matched samples, but they differ in their methodology and sensitivity to the data. Here are the key differences:
- Methodology:
- Wilcoxon Signed Rank Test:
- This test considers both the magnitude and the sign of the differences between paired observations. It ranks the absolute differences, ignores zeroes (no difference), and then uses the sum of ranks for either the positive or negative differences (depending on the hypothesis) as the test statistic.
- Sign Test:
- The Sign Test only considers the sign of the differences between paired observations, not their magnitude. It simply counts the number of positive and negative differences, ignoring zeroes. The test statistic is the smaller of these counts.
- Wilcoxon Signed Rank Test:
- Sensitivity & power:
- The Wilcoxon Signed Rank Test is generally more powerful than the Sign Test because it takes into account the magnitude of the differences. This means that the Wilcoxon test is more likely to detect a true effect when one exists.
- The Sign Test, while less powerful, can be useful when the exact magnitudes of the differences are not reliable or are not of primary concern.
- Interpretation:
- In the Wilcoxon signed rank test, a significant result suggests a shift in the median of the differences between pairs.
In the Sign Test, a significant result suggests a consistent direction of difference (either positive or negative), but it says nothing about the magnitude of this difference.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me