Linear Regression in Machine Learning: Python Examples

December 15, 2023 by Ajitesh Kumar · 2 Comments
Multiple linear regression example

Last updated: 15th Dec, 2023

In this post, the linear regression concepts in machine learning is explained with multiple real-life examples. Two types of regression models (simple/univariate and multiple/multivariate linear regression) are taken up for sighting examples. In addition, Python code examples are used for demonstrating training of simple linear and multiple linear regression models.  In case you are a machine learning or data science beginner, you may find this post helpful enough. You may also want to check a detailed post – What is Machine Learning? Concepts & Examples.

What is Linear Regression?

Linear regression is a machine learning concept that is used to build or train the models for solving supervised learning problems related to predicting continuous numerical value. Recall that the supervised learning problems represent the class of the problems where the value (data) of the independent or predictor variable (features) and the dependent or response variables are already known. The known values of the dependent and independent variables are used to come up with a mathematical model also called as linear regression equation which is later used to make the predictions.

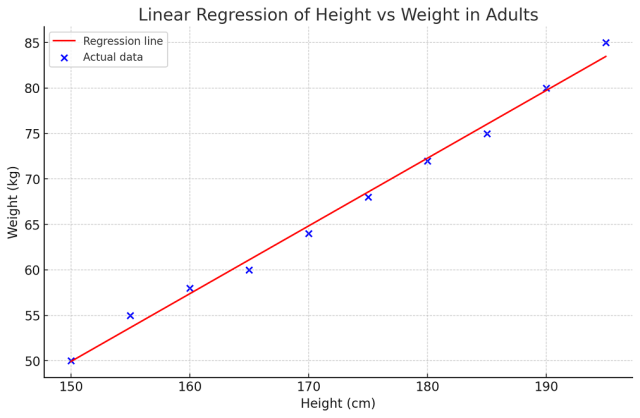
The following is an example of simple linear or univariate linear regression analysis representing the relationship between the height and weight in adults using the regression line. The regression line is superimposed over the scatterplot of height vs weight to showcase the linear relationship.

linear regression model representing wiehgt vs height

Building linear regression models represents determining the value of output (dependent/response variable) as a function of the weighted sum of coefficients and input features (independent / predictor variables) while making use of historical dataset  This data is used to determine the most optimum value of the coefficients of the independent variables.

Here are few assumptions which need to be kept in mind when building linear regression models:

  • There is a linear relationship between input and output variables.
  • The noise or residual error is well-mannered (normal or Gaussian distribution).

Let’s say, there is a numerical response variable, Y, and one or more predictor variables X1, X2, etc. Let’s say, hypothetically speaking, the following represents the relationship between Y and X in the real world.

$\Large Y_i = f(X) + error$

Where $Y_i$ is the actual or observed value and  f is some fixed but unknown function of X1 and X2. We need to find this function based on training the model that would estimate or predict some value, $\hat{Y_i}$. The difference between the actual or observed value, $Y_i$ and the predicted value, $\hat{Y_i}$ is called as the error or residual. When the unknown function is a linear function of X1 and X2, the Y becomes a linear regression function or model such as the following. Note that the error term averages out to be zero.

$\Large \hat{Y_i} = b_0 + b_1*X_1 + b_2*X_2$

In the above equation, different values of Y and X1, and X2 are known during the model training phase. As part of training the model, the most optimal value of coefficients b1, b2, and b0 are determined based on the least square regression algorithm. The least-squares method algorithm is used to find the best fit for a set of data points by minimizing the sum of the squared residuals or square of error of points (actual values representing the response variable) from the points on the plotted curve (predicted value). This is shown below.

If $Y_i$ is the ith observed value and $\hat{Y_i}$ is the ith predicted value, then the ith residual or error value is calculated as the following:

$\Large e_i = Y_i – \hat{Y_i} $

The residual sum of squares can then be calculated as the following:

$\Large RSS = {e_1}^2 + {e_2}^2 + {e_3}^2 + … + {e_n}^2$

In order to come up with the optimal linear regression model, the least-squares method as discussed above represents minimizing the value of RSS (Residual sum of squares).

In order to select the most appropriate variables / features such as X1, X2, etc., the hypothesis is laid down around the coefficient for each of the variables / features. The null hypothesis is that the value of coefficients are 0. This means that the value of b0, b1, b2, etc. are 0. The alternate hypothesis is that the coefficients are not equal to zero. In this manner, the dependent variable holds good. T-statistics is used for hypothesis testing and reject the null hypothesis (b0, b1 or b2 = 0) if appropriate. The following is the formula of the t-statistics with n-2 degree of freedom. For more details, read my related blog –  linear regression and t-test.

$\Large t = \frac{b_i}{StandardError(b_i)}$

Types of Linear Regression Models

There are two different types of linear regression models. They are the following:

  • Simple linear regression: The following represents the simple linear regression where there is just one independent variable, X, which is used to predict the dependent variable Y.
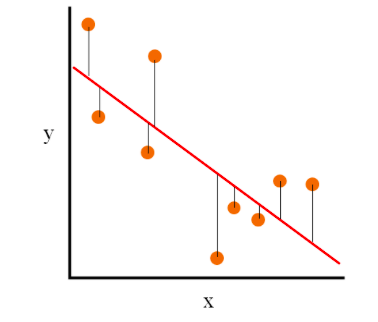
    Simple linear regression example

    Fig 1. Simple linear regression

    The following mathematical formula represents the simple regression model:

    $\Large Y_i = b*{X_i} + b_0 + error$

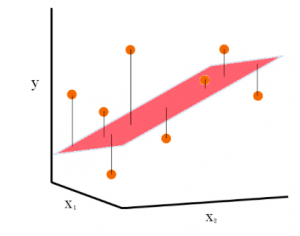
  • Multiple linear regression: The following represents the multiple linear regression where there are two or more independent variables (X1, X2) that are used for predicting the dependent variable Y.
    Multiple linear regression example

    Fig 2. Multiple linear regression

The following formula can be used to represent a typical multiple regression model:

$\Large Y_i = b_0 + b_1*X_1 + b_2*X_2 + b_3*X_3 + … + b_n*X_n + error$

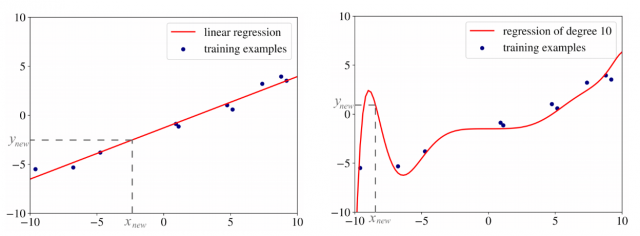
We have seen that the linear regression model is learned as the linear combination of features to predict the value of the target or response variable. However, we could use a square or some other polynomial to combine the values of features and predict the value of the target variable. This would turn out to be a more complex model than the linear one. One of the reasons why the linear regression model is more useful than the polynomial regression is the fact that the polynomial regression tends to overfit. The picture below represents the linear vs polynomial regression model and represents how the polynomial regression model tends to overfit.

linear regression model vs polynomial regression 1

Simple Linear Regression – Problem & Python Example

Before looking into the Python implementation of simple linear regression machine learning model, let’s consider the problem of predicting the marks of a student based on the number of hours he/she put into the preparation. Although at the outset, it may look like a problem that can be modeled using simple linear regression, it could turn out to be a multiple linear regression problem depending on multiple input features. Alternatively, it may also turn out to be a non-linear problem. However, for the sake of example, let’s consider this as a simple linear regression problem.

However, let’s assume for the sake of understanding that the marks of a student (M) do depend on the number of hours (H) he/she put up for preparation. The following formula can represent the model:

Marks = function (No. of hours)

=> Marks = m*Hours + c

The best way to determine whether it is a simple linear regression problem is to do a plot of Marks vs Hours. If the plot comes like below, it may be inferred that a linear model can be used for this problem.

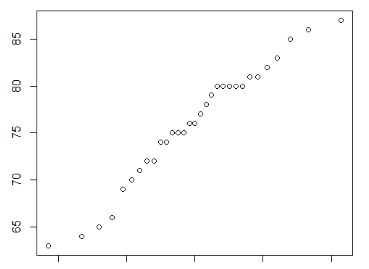
Plot representing simple linear model

Fig 3. Plot representing a simple linear model for predicting marks

The data represented in the above plot would be used to find out a line such as the following which represents a best-fit line. The slope of the best-fit line would be the value of “m”.

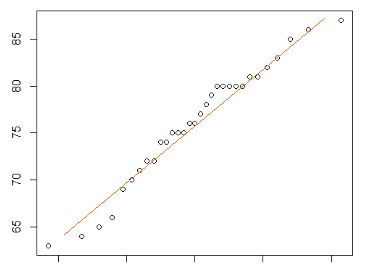
Plot representing simple linear model with regression line

Fig 4. Plot representing a simple linear model with a regression line

The value of m (slope of the line) can be determined using an objective function which is a combination of the loss or cost function and a regularization term. For simple linear regression, the objective function would be the summation of Mean Squared Error (MSE). MSE is the sum of squared distances between the target variable (actual marks) and the predicted values (marks calculated using the above equation). The best fit line would be obtained by minimizing the objective function (summation of mean squared error).

Python Implementation for Simple Linear Regression Model

The following is the python code implementation of simple linear regression model for predicting marks based on the number of study hours. The Mean Squared Error (MSE) of the model on the test set is used to assess the performance of the regression model. This MSE value represents the average squared difference between the actual and predicted marks, indicating the accuracy of the model. A lower MSE value would suggest a more accurate model.

from sklearn.linear_model import LinearRegression
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# Hypothetical data
np.random.seed(0)
hours = np.random.uniform(0, 10, 100)  # Number of hours
marks = np.random.uniform(0, 100, 100)  # Marks obtained

# Creating a DataFrame
data = pd.DataFrame({
    'Hours': hours,
    'Marks': marks
})

# Defining the independent variable (feature) and the dependent variable (target)
X = data[['Hours']]
y = data['Marks']

# Splitting the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Creating the Linear Regression model
model = LinearRegression()

# Training the model
model.fit(X_train, y_train)

# Predicting on the test set
y_pred = model.predict(X_test)

# Calculating Mean Squared Error
mse = mean_squared_error(y_test, y_pred)

# Coefficient (m) and Intercept (c)
m = model.coef_[0]
c = model.intercept_

m, c, mse

Multiple Linear Regression – Problem & Python Example

Before looking into the Python implementation of multiple linear regression, let’s look at a related problem of predicting weight reduction based on different parameters (hence, multiple regression). The problem of predicting weight reduction in form of the number of KGs reduced, hypothetically, could depend upon input features such as age, height, the weight of the person, and the time spent on exercises, .

Weight Reduction = Function(Age, Height, Weight, TimeOnExercise)

=> Shoe-size = b1*Height + b2*Weight + b3*age + b4*timeOnExercise + b0

As part of training the above model, the goal would be to find the value of b1, b2, b3, b4, and b0 which would minimize the objective function. The objective function would be the summation of mean squared error which is nothing but the sum of the square of the actual value and the predicted value for different values of age, height, weight, and timeOnExercise.

Python Implementation for Multiple Linear Regression Model

The following is the python code implementation of multiple linear regression machine learning model for predicting weight reduction based on age, height, weight, and time spent on exercises. As like simple linear regression model, the MSE of the model on the test set is used to assess the regression model performance. 

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# Hypothetical data for demonstration purposes
# Let's create a dataset with 100 samples
np.random.seed(0)
age = np.random.randint(18, 65, 100)
height = np.random.uniform(1.5, 2.0, 100)
weight = np.random.uniform(50, 100, 100)
time_on_exercise = np.random.uniform(0.5, 2.5, 100)
weight_reduction = np.random.uniform(0, 10, 100)  # This will be our target variable

# Creating a DataFrame
data = pd.DataFrame({
    'Age': age,
    'Height': height,
    'Weight': weight,
    'TimeOnExercise': time_on_exercise,
    'WeightReduction': weight_reduction
})

# Defining the independent variables (features) and the dependent variable (target)
X = data[['Age', 'Height', 'Weight', 'TimeOnExercise']]
y = data['WeightReduction']

# Splitting the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Creating the Linear Regression model
model = LinearRegression()

# Training the model
model.fit(X_train, y_train)

# Predicting on the test set
y_pred = model.predict(X_test)

# Calculating Mean Squared Error
mse = mean_squared_error(y_test, y_pred)

# Coefficients (b1, b2, b3, b4) and Intercept (b0)
b1, b2, b3, b4 = model.coef_
b0 = model.intercept_

b1, b2, b3, b4, b0, mse

Key Terminologies for Regression Models

The following are some key terminologies in relation to measuring the residuals and performance of the linear regression machine learning models:

  • Root Mean Square Error (RMSE): Root Mean Square Error (RMSE) is a measure of how well a linear regression model fits the data. It is calculated by taking the squared difference between the predicted values and the observed values, finding an average of all the differences, and then taking the square root of this number. The lower the RMSE value, the better fit of our model to the data. The following is the formula of RMSE where $y_i$ represents the actual values, $\hat{y}_i$ represents the predicted values and n represents the number of observations.

    $\Large \text{RMSE} = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i – \hat{y}_i)^2}$
  • R-Squared: R-Squared is a statistical measure that represents how well the linear regression model fits the data. It is also known as the coefficient of determination. It is a statistic that measures the proportion of variation in the dependent variable (the y-axis) that can be explained by the independent variables (the x-axis). The R-squared value ranges between 0 and 1, with 1 indicating a perfect fit. A higher R-squared value indicates that more of the variance in the dependent variable can be explained by the independent variables. The following is R-Squared formula where $y_i$ represents the actual values, $\hat{y}_i$ represents the predicted values, $\bar{y}$ represents the mean of actual values, and n represents the number of observations.

    $\Large R^2 = 1 – \frac{\sum_{i=1}^{n}(y_i – \hat{y}i)^2}{\sum{i=1}^{n}(y_i – \bar{y})^2}$
  • Residual standard error (RSE): Residual Standard Error (RSE) is a measure of how well linear regression models fit the data. It is calculated by taking the sum of the squared residuals (the differences between the observed values and predicted values), dividing it by the degrees of freedom, then taking its square root. The RSE provides an indication of how much variation there is in the data that cannot be explained by the regression model. Lower RSE values indicate better fits to the data.

Assumptions for Linear Regression Models

While working with linear regression models, some of the following assumptions are made about the data. If these assumptions are violated, the results of linear regression analysis might not turn out to be valid:

  • Linearity: The relationship between the predictor and the response variable would resemble a straight line. This assumption is checked by scatter plotting the data. If the plot resembles a shape other than the straight line, it might require transforming one or more variables.
  • Data appropriateness: The values of response variable must be continuous and unbounded (cover a wide range of values). The values of independent variables must as well be continuous and dichotomous. Categorical variables having more than two values must be converted into a series of dichotomous dummy variables.
  • Data independence: Each of the value of response variable would be independent of each other’s value. This assumption can be checked against scenario such as time-dependency or values of response variables forming clusters, etc.
  • Data distribution: It is assumed that the response variable is normally distributed. In other words, the response variable follows Gaussian distribution. The distribution can be checked by creating a histogram (eyeballing the data) and by a statistical test for normality such as the Kolmogorov-Smirnov.
  • Homoscedasticity: The prediction errors remain nearly constant & consistent regardless of how far the data range extends. It essentially means that the prediction errors don’t change with the value of response variable. For instance, for smaller values of response variable (Y), the prediction error will be small and for larger values, it becomes large. This can be ascertained by plotting standardized residuals against their corresponding predicted values – any significant changes in error size would be immediately visible.

Linear Regression Models & Problems Examples

The following represents some real-world problems’ examples / use cases where linear regression machine learning models can be used:

  • Forecasting sales: Organizations often use linear regression models to forecast future sales. This can be helpful for things like budgeting and planning. Algorithms such as Amazon’s item-to-item collaborative filtering are used to predict what customers will buy in the future based on their past purchase history.
  • Cash forecasting: Many businesses use linear regression to forecast how much cash they’ll have on hand in the future. This is important for things like managing expenses and ensuring that there is enough cash on hand to cover unexpected costs.
  • Analyzing survey data: Linear regression can also be used to analyze survey data. This can help businesses understand things like customer satisfaction and product preferences. For example, a company might use linear regression to figure out how likely people are to recommend their product to others.
  • Stock predictions: A lot of businesses use linear regression models to predict how stocks will perform in the future. This is done by analyzing past data on stock prices and trends to identify patterns.
  • Predicting consumer behavior: Businesses can use linear regression to predict things like how much a customer is likely to spend. Regression models can also be used to predict consumer behavior. This can be helpful for things like targeted marketing and product development. For example, Walmart uses linear regression to predict what products will be popular in different regions of the country.
  • Analysis of relationship between variables: Linear regression can also be used to identify relationships between different variables. For example, you could use linear regression to find out how temperature affects ice cream sales.

Frequently Asked Questions (FAQs)

The following is a list of FAQs related to linear regression algorithm / machine learning models.

  • Is linear regression supervised or unsupervised?
    • Linear regression is a supervised learning method.
  • Is linear regression a classification algorithm?
  • Is linear regression sensitive to outliers?
    • Linear regression can be sensitive to outliers because it tries to fit a linear model to the data by minimizing the sum of the squared differences between the observed values and the model’s predictions. Outliers are data points that deviate significantly from the trend of the rest of the data. Since the fitting process involves squaring the differences, even a single outlier with a large deviation can disproportionately affect the model’s coefficients, pulling the regression line toward itself and potentially leading to a less accurate model for the rest of the data.
  • Is linear regression model a machine learning model?
    • It is a statistical model and also considered a machine learning model when used for predictive tasks.
  • Is linear regression a neural network?
    • Linear regression is not a neural network; it’s a simpler model based on a linear predictor function.
  • Is z-test used with linear regression?
    • The Z-test is not commonly used with linear regression. Instead, the t-test is typically used to determine the statistical significance of each coefficient in the regression model. The t-test evaluates whether the estimated coefficient for each independent variable differs significantly from zero, which would suggest that the variable has a predictive effect on the dependent variable. The Z-test is used when the sample size is large (typically greater than 30) and the population variance is known, which is generally not the case in linear regression problems.
  • What are residuals in linear regression?
    • Residuals in linear regression are the differences between the observed values of the dependent variable (the actual data points) and the values predicted by the regression model. They are essentially the errors of the prediction, indicating how far off the model’s predictions are from the actual values. Analyzing the pattern of residuals can provide insights into the adequacy of the model, such as indicating whether the linear model is appropriate or if there are other factors at play that the model is not capturing.
  • Is linear regression parametric?
    • Yes, linear regression is a parametric method. It makes assumptions about the form of the function that relates the independent and dependent variables, specifically assuming a linear relationship.
  • Is overfitting a problem for linear regression model in achieving high performance?
    • Yes, overfitting can be a problem for linear regression models, especially if they include too many features or are overly complex relative to the size of the data set.

References – Further Reads

Here are some of my other posts in relation to linear regression:

Summary

In this post, you learned about linear regression, different types of linear regression machine learning models, and examples for each one of them. It can be noted that a supervised learning problem where the output variable is linearly dependent on input features could be solved using linear regression models. Linear regression models get trained using a simple linear or multiple linear regression algorithm which represents the output variable as the summation of weighted input features.

Ajitesh Kumar
Follow me
Latest posts by Ajitesh Kumar (see all)

Ajitesh Kumar

I have been recently working in the area of Data analytics including Data Science and Machine Learning / Deep Learning. I am also passionate about different technologies including programming languages such as Java/JEE, Javascript, Python, R, Julia, etc, and technologies such as Blockchain, mobile computing, cloud-native technologies, application security, cloud computing platforms, big data, etc. For latest updates and blogs, follow us on Twitter. I would love to connect with you on Linkedin. Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com
Posted in AI, Data Science, Machine Learning, statistics. Tagged with , , , , .

2 Responses

Leave a Reply

Your email address will not be published. Required fields are marked *