Last updated: 21st Jan, 2024
Machine Learning (ML) models are designed to make predictions or decisions based on data. However, a common challenge, data scientists face when developing these models is ensuring that they generalize well to new, unseen data. Generalization refers to a model’s ability to perform accurately on new, unseen examples after being trained on a limited set of data. When models don’t generalize well, they commit errors. These errors are called generalization errors. In this blog, you will learn about different types of generalization errors, with examples, and walk through a simple Python demonstration to illustrate these concepts.
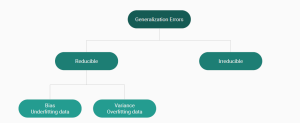
Types of Generalization Errors
Generalization errors in machine learning / data science can be broadly divided into two categories: reducible and irreducible errors.
Reducible Errors
Reducible errors in machine learning are those parts of the prediction error that can be reduced or eliminated by improving the model. They consist of two main components: bias and variance. These errors are termed “reducible” because they are due to the model’s inability to capture the true relationship in the training data, and theoretically, they can be minimized with better model selection, more data, or improved training procedures.
- Bias (Underfitting Data): Bias occurs when a model is too simple to capture the complexities of the dataset. It’s like trying to fit a straight line into a curvy path – it just doesn’t match well. For example, if we’re trying to predict housing prices based on size alone, ignoring other factors like location and age, our model will likely have a high bias.
- Variance (Overfitting Data): Variance occurs when a model is too complex and captures the noise in the training data to the extent that it negatively impacts the performance of new data. It’s akin to memorizing the path instead of understanding the direction. An example would be a model that predicts stock prices by closely following the historical fluctuations, including the anomalies, which don’t generalize well when the market conditions change. Check out the post: Bias-variance tradeoff in machine learning.
Irreducible Errors
Irreducible errors are those that cannot be reduced by any model due to the inherent noise or randomness in the data itself. No matter how sophisticated the model, there will always be some level of error due to factors we cannot predict or have not measured.
Understanding Generalization Errors: Example – Predicting House Prices
To demonstrate these concepts, let’s take up a data science problem of predicting house prices based on various features like size, location, number of rooms, age, etc. We will train a model using Python, calculate metrics to determine the generalization error, and identify the errors as bias or variance.
We will train two models: a simple linear regression model that may underfit and a complex decision tree that may overfit.
A linear regression model will be trying to predict housing prices regardless of features like location, number of rooms, or age of the house. This model assumes a simple relationship and would likely have high bias as it oversimplifies the problem.
A decision tree would tend to grow very deep such that it would learn the training data including the noise. This model will likely have high variance and perform poorly on unseen data because it’s too tailored to the specific examples in the training set.
Let’s look at the Python code with models trained on California housing dataset.
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.tree import DecisionTreeRegressor
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()
X, y = housing.data, housing.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Linear Regression Model
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)
# Decision Tree Regressor
dt_model = DecisionTreeRegressor(max_depth=10)
dt_model.fit(X_train, y_train)
# MSE on training & test dataset for Linear Regression
y_train_pred_lr = lr_model.predict(X_train)
mse_train_lr = mean_squared_error(y_train, y_train_pred_lr)
y_pred_lr = lr_model.predict(X_test)
mse_lr = mean_squared_error(y_test, y_pred_lr)
# MSE on training and test dataset for Decision Tree
y_train_pred_dt = dt_model.predict(X_train)
mse_train_dt = mean_squared_error(y_train, y_train_pred_dt)
y_pred_dt = dt_model.predict(X_test)
mse_dt = mean_squared_error(y_test, y_pred_dt)
# Output the MSE values for training and test dataset for linear regression
print(f"Linear Regression Training MSE: {mse_train_lr}")
print(f"Linear Regression Test MSE: {mse_lr}")
# Output the MSE on the training and test dataset for decision tree model
print(f"Decision Tree Training MSE: {mse_train_dt}")
print(f"Decision Tree Test MSE: {mse_dt}")
The following gets printed as a result of executing the above code:
Linear Regression Training MSE: 0.5179331255246699
Linear Regression Test MSE: 0.5558915986952422
Decision Tree Training MSE: 0.2208657912045762
Decision Tree Test MSE: 0.42106415822823845
Let’s analyze and understand the reducible errors concept of bias and variance.
The output of the Mean Squared Error (MSE) for both the Linear Regression and the Decision Tree models on the training and test sets provides valuable insights into their performance and whether they suffer from high bias or high variance.
Linear Regression Model Error Analysis (High Bias):
- Training MSE: 0.5179331255246699
- Test MSE: 0.5558915986952422
The MSE for the Linear Regression model on the training data and the test data are quite close to each other, and both are moderately high. This suggests that the model is consistent across both datasets, which is a good sign in terms of variance. However, since the error is not particularly low on either, it indicates that the model may not be complex enough to capture all the underlying relationships in the data. This is indicative of high bias. The model is underfitting the dataset, meaning that it is too simplistic and does not have enough capacity to learn the details and the complexity of the data.
Decision Tree Model Error Analysis (High Variance):
- Training MSE: 0.2208657912045762
- Test MSE: 0.42106415822823845
The Decision Tree model’s MSE on the training data is significantly lower than its MSE on the test data. This large discrepancy suggests that while the Decision Tree model is able to fit the training data very well (potentially too well), it does not perform as well on the test data. This is a classic sign of high variance, which indicates that the model is overfitting the training data. It has learned the noise in the training set to the extent that it negatively impacts its performance on unseen data.
Handling Generalization Reducible Errors (Bias & Variance)
Now that we know how to determine whether the model is having which type of reducible generalization error such as bias or variance, lets learn how to address these generalization errors.
To Address High Bias in Linear Regression:
- Consider more complex models that can capture the relationships in the data more effectively.
- Perform feature engineering to create new features or transform existing ones to provide the model with more information.
- Look into interaction terms or polynomial features that could capture non-linear relationships.
To Address High Variance in Decision Tree:
- Simplify the model by reducing the maximum depth or imposing other constraints to prevent it from growing overly complex.
- Use ensemble methods like Bagging or Random Forests to average out the predictions and reduce overfitting.
- Implement cross-validation to ensure that the model’s performance is consistent across different subsets of the training data.
- Use regularization techniques or pruning to reduce the complexity of the tree after it has been trained.
FAQs on Generalization Errors
The following are some of the most common frequently asked questions related to generalization errors in machine learning:
- What is the difference between generalization error and training error?
- Training error reflects a model’s accuracy on the dataset it was trained on, serving as a measure of how well the model has learned from its training examples. In contrast, generalization error estimates the model’s performance on unseen data, indicating its ability to apply learned patterns to new instances. The crux of a successful model lies in its low generalization error, which is crucial since it determines the model’s effectiveness in real-world applications. A substantial difference between low training error and high generalization error often signals overfitting, where the model fails to generalize beyond the training data.
- What is the difference between generalization error and test error?
- Generalization error and test error are often used interchangeably in machine learning to describe a model’s performance on unseen data. However, generalization error is a broader concept referring to a model’s expected error rate on any new data, while test error specifically measures the model’s error rate on a particular set aside dataset. Both aim to provide an estimate of how a model will perform in real-world scenarios, but the generalization error encompasses a wider range of potential unseen data beyond the specific test set used.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me