Last updated: 24th August, 2024
The performance of the machine learning models on unseen datasets depends upon two key concepts called underfitting and overfitting. In this post, you will learn about these concepts and more. In addition, you will also get a chance to test your understanding by attempting the quiz. The quiz will help you prepare well for data scientist interviews.
Introduction to Overfitting & Underfitting
Assuming an independent and identically distributed (I.I.d) dataset, when the prediction error on both the training and validation dataset is high, and the difference between them is very minimal, the model is said to have underfitted. In this scenario, it becomes cumbersome to reduce the training error. The model is said to be too simple to capture different patterns in the data. This is called underfitting the model or model underfitting.
When the prediction error on the validation dataset is quite high or higher than the training dataset, the model can be said to have overfitted. In other words, when there is a lot of gap between the training and validation error, the model can be said to have been overfitted. This is called model overfitting. Model overfitting is found to happen when model fits the training data too closely, thereby learning noise and outliers present in the data rather than the underlying pattern. As a result, the model performs well on the training data but poorly on unseen or test data.
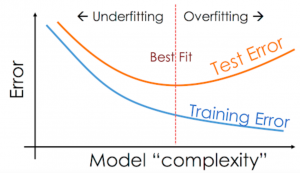
The picture below represents the case of underfitting and overfitting classification model. Note that in the overfitted model, the separator divides the data most accurately.
What are different scenarios in which machine learning models overfitting can happen?
Overfitting of machine learning models happens when the training error is much less than the validation/generalization error. This can happen in some of the following scenarios:
- When models are trained using too many parameters to model the training data.
- If the hypothesis space searched by the learning algorithm is high. This happens when the model capacity is high. For example, in the case of polynomial regression, the model capacity is very high because the hypotheses space is very high. Let’s try and understand what is meaning of hypothesis space is and what is meaning of searching hypothesis space. If the learning algorithm used for fitting the model can have a large number of different parameters and hyperparameters, and, could be trained with different datasets (called training datasets) extracted from the same dataset, this could result in a large number of models (hypothesis – h(X)) fit on the same data set. Recall that a hypothesis is an estimator of the target function. Thus, on the same dataset, a large number of models can be fit. This is called a larger hypothesis space. The learning algorithm in such a scenario can be said to have access to a larger hypothesis space. Given this larger hypothesis space, there is a high possibility for the model to overfit the training dataset.
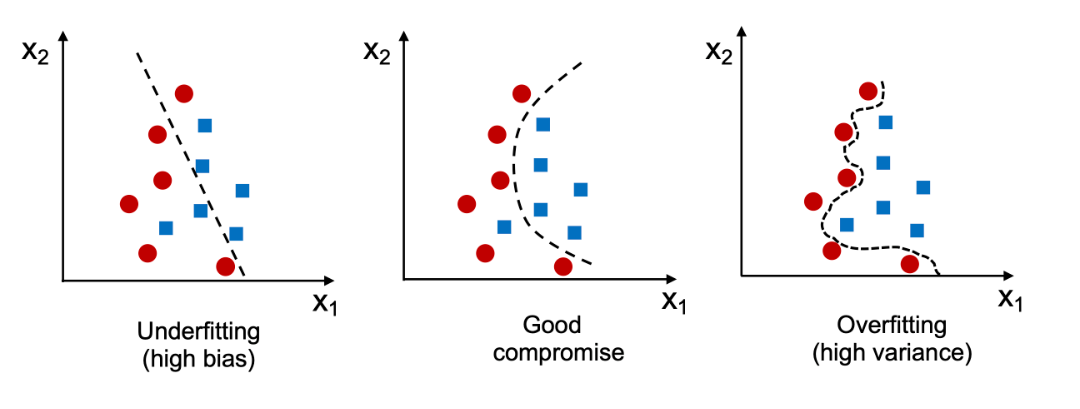
- The smaller number of samples we have in the training dataset, the more likely is the possibility of encountering overfitting. As the number of training samples increases, the generalization error is found to typically decrease. Given that the overfitting is determined by the gap between the generalization and training error, the decrease in generalization error can result in a reduction in overfitting. In order to find whether the overfitting can be managed by increasing training data samples, you can plot the learning curve. To construct a learning curve, you need to train the model to different training set sizes (10 percent, 20 percent, and so on) and evaluate the trained model on the same fixed-size validation or test set. In the plot shown below, the validation accuracy increases as the training set sizes increase. This indicates that we can improve the model’s performance by collecting more data.
What are different scenarios in which machine learning models underfitting can happen?
Underfitting of machine learning models happens when you are not able to reduce the training error. This can happen in some of the following scenarios:
- When the training set has far fewer observations than variables, this may lead to underfitting or low bias machine learning models. In such cases, the machine learning models cannot find any relationship between input data and the response variable because the model is not complex enough to model the data.
- When machine learning algorithm cannot find any pattern between training and testing set variables which may happen in the high-dimensional dataset or a large number of input variables. This could be due to insufficient machine learning model complexity, limited available training observations for learning patterns, limited computing power that limits machine learning algorithms’ ability to search for patterns in high dimensional space, etc.
Here is a diagram that represents the underfitting vs overfitting in form of model performance error vs model complexity.
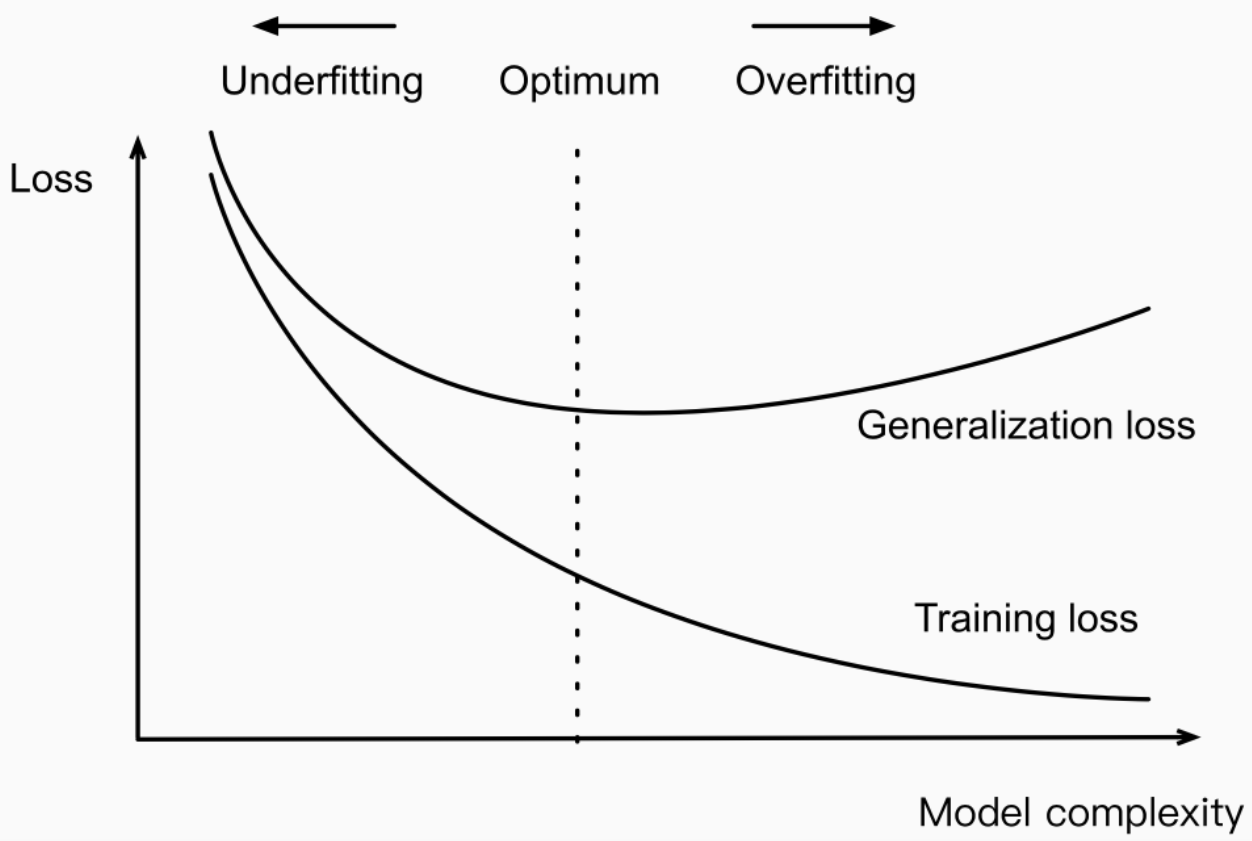
In the above diagram, when the model complexity is low, the training and generalization error are both high. This represents the model underfitting. When the model complexity is very high, there is a very large gap between training and generalization error. This represents the case of model overfitting. The sweet spot is in between, represented using a dashed line. At the sweet spot, e.g., the ideal model, there is a smaller gap between training and generalization error.
In order to create a model with decent performance, one should aim to select a decently complex model while avoiding using insufficient training samples.
Managing Underfitting / Overfitting by Managing Model Complexity
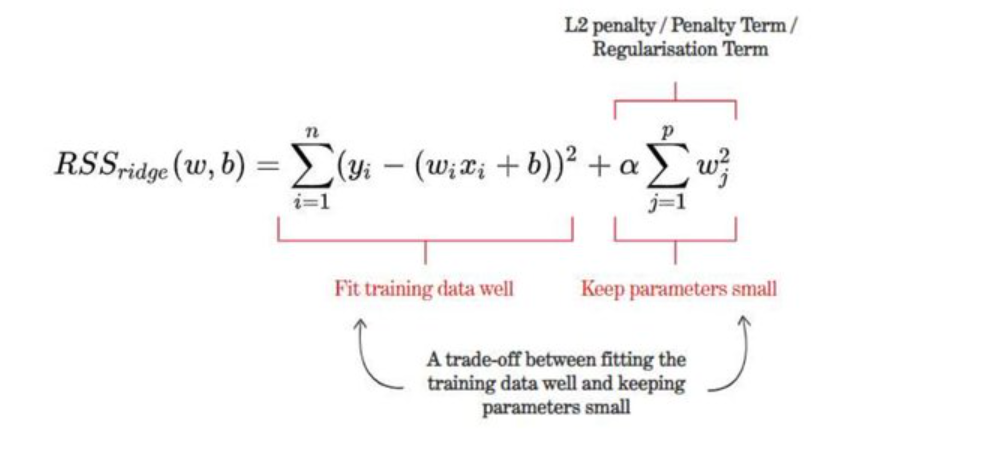
The way to manage underfitting and overfitting of model in an optimal manner is to manage the model complexity. One of the most important reasons why model overfitting happens is model complexity which happens because of various different reasons such as a large number of model parameters. In such scenarios, the model complexity happening due to a large number of parameters can be resolved using regularization techniques such as L1 or L2 norm. Recall that the regularization technique is used for reducing model overfitting by reducing model complexity. Model complexity is reduced by adding L1 or L2 norm of the weight vector as a penalty term to the problem of minimizing loss. Thus, with one of the L1 or L2 norms, the objective function becomes as minimizing the sum of prediction loss and the penalty term instead of just minimizing the prediction loss to reduce model complexity and hence overfitting. L1 norm is used in what is called LASSO (least absolute shrinkage and selection operator) regression which penalizes several parameters by reducing their value to zero. This technique is popular for feature selection. In the L2 norm which is used in Ridge regression, the model parameters are reduced to very minimal. Various machine learning techniques, including validation curves and cross-fold plots, can be used to spot overfitting.
The ridge regression loss function below represents the L2 penalty term added to loss function of linear regression.
When there are more features than examples, linear models tend to overfit. However, when there are more examples than the features, linear models can be counted upon not to overfit. However, the same is not true for deep neural networks. They tend to overfit even after the fact that there are a lot more examples than the features.
Interview Questions on Underfitting & Overfitting
Before getting into the quiz, let’s look at some of the interview questions in relation to overfitting and underfitting concepts:
- What are overfitting and underfitting?
- What is the difference between overfitting and underfitting?
- Illustrate the relationship between training/test error and model complexity in the context of overfitting & underfitting?
Here is the quiz which can help you test your understanding of overfitting & underfitting concepts and prepare well for interviews.
Results
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
#1. Assuming I.I.d training and test data, for some random model that has not been fit on the training dataset, the training error is expected to be _________ the test error
#2. Assuming I.I.d training and test data, for the model that has been fit on the training dataset, the training error is expected to be _________ the test error
#3. The training error or accuracy of the model fit on the I.I.d training and test data set provides an __________ biased estimate of the generalization performance
#4. In case of underfitting, both the training and test error are _________
#5. In case of overfitting, the gap between training and test error is ___________
#6. In case of overfitting ,the training error is _________ than test error
#7. Given the larger hypothesis space, there is a higher tendency for the model to ________ the training dataset
#8. Given the following type of decision tree model, which may result in model underfitting?
#9. Given the following type of decision tree model, which may result in model overfitting?
#10. Given the following models trained using K-NN, the model which could result in overfitting will most likely have the value of K as ___________
#11. Given the following models trained using K-NN, the model which could result in underfitting will most likely have the value of K as ___________
#12. A model suffering from underfitting will most likely be having _____________
#13. A model suffering from overfitting will most likely having
That’s all for now on machine learning model overfitting, model underfitting, how they are related to model complexity, and how to reduce model overfitting and underfitting. Remember that a good rule of thumb is to keep your models simple so they are less likely to suffer from overfitting or underfitting problems. You can use the regularization techniques such as L1 norm or L2 norm to reduce model complexity and hence model overfitting. If you have any questions about these concepts or want help implementing them, don’t hesitate to reach out. We would be happy to assist you further!
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
noice