In this post, you will learn about nested cross validation technique and how you could use it for selecting the most optimal algorithm out of two or more algorithms used to train machine learning model. The usage of nested cross validation technique is illustrated using Python Sklearn example.
When it is about selecting models trained with a particular algorithm with most optimal combination of hyper parameters, you can adopt the model tuning techniques such as some of the following:
The following topics get covered in this post:
- Why nested cross-validation?
- Nested cross-validation with Python Sklearn example
Why Nested Cross-Validation?
Nested cross-validation technique is used for estimating the generalization error of the model along with the search of most optimal combination of hyper parameters value. It is seen that the usage of nested cross-validation technique results in the unbiased true error of the estimate relative to the test data set. Model selection with non-nested cross validation results in the use of the same data to tune model hyper parameters and evaluate the model performance. Information may thus leak into the model and overfit the data. The magnitude of this effect is primarily dependent on the size of the dataset and the stability of the model.
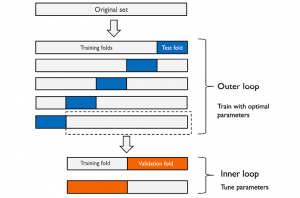
In nested cross-validation, there is an outer k-fold cross-validation loop which is used to split the data into training and test folds. In addition to the outer loop, there is an inner k-fold cross-validation loop hat is used to select the most optimal model using the training and validation fold. Here is the diagram representing the same:
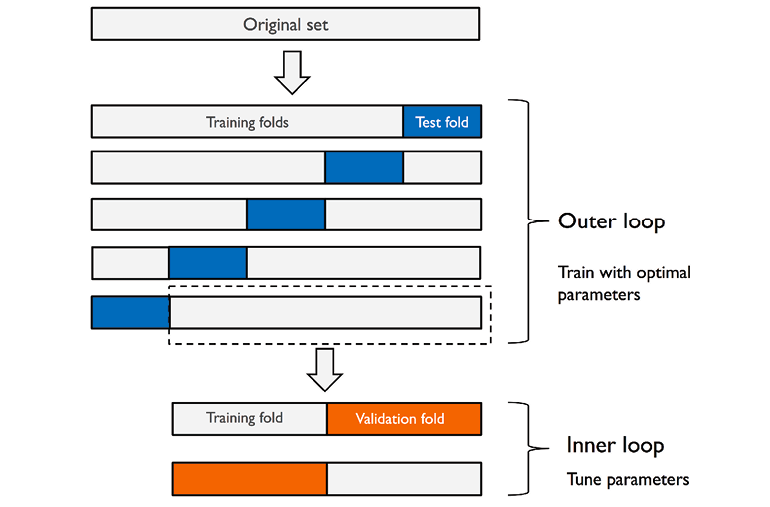
As shown in the above diagram (courtesy Dr Sebastian Raschka blog), the score of the model is maximised by fitting a model on the training set and testing the model with most optimal combination of hyper parameters on validation set. Two-folds (2-folds CV) are shown to be used in the above diagram. The Sklearn code makes use of GridSearchCV for selecting the optimal combination of hyper parameters on 2 folds (2-folds CV). Once the most optimal model is selected using the inner loop, the generalization error of the model is estimated using 5-folds (5-fold CV) cross validation technique in the outer loop. The Sklearn cross_val_score is used for used for estimating the generalization error. This technique of using 2-folds for model selection and 5 folds for estimating generalization error can be called as 5×2 cross-validation. The nested 5×2 cross-validation technique is used for algorithm selection when working with large computational datasets.
Nested Cross-validation with Python Sklearn Example
In this section, you will learn the usage of nested cross-validation technique with GridSearchCV used in the inner loop for model selection, and, StratifiedKFold cross validation in the outer loop for estimating generalization error. The algorithm such as support vector classifier (sklearn.svm SVC) and logistic regression (sklearn.linear_model LogisticRegression) is evaluated using 5×2 cross-validation technique.
Here is the nested 5×2 cross validation technique used to train model using support vector classifier algorithm. The accuracy of the model comes out to be 0.980 +/- 0.017
pipeline = make_pipeline(StandardScaler(), SVC(random_state=1))
#
# Create the parameter grid
#
param_grid = [{
'svc__C': [0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1.0, 10.0],
'svc__kernel': ['linear']
}, {
'svc__C': [0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1.0, 10.0],
'svc__gamma': [0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1.0, 10.0],
'svc__kernel': ['rbf']
}]
#
# Create the Grid Search estimator instance for selecting model using
# 2-fold StratifiedKFold cross validation
#
gs = GridSearchCV(estimator=pipeline, param_grid = param_grid,
cv = 2, scoring = 'accuracy', n_jobs = 1, refit = True)
#
# Calculate the generalization error / accuracy
#
scores = cross_val_score(gs, X_train, y_train, scoring='accuracy', cv=5)
#
# Print the mean scores and standard deviation
#
print('CV accuracy: %.3f +/- %.3f' % (np.mean(scores), np.std(scores)))
Here is the nested 5×2 cross validation technique used to train model using Logistic Regression algorithm. The accuracy of the model comes out to be 0.982 +/- 0.015
#
# Pipeline created using Logistic Regression
#
pipeline = make_pipeline(StandardScaler(),
LogisticRegression(penalty='l2', solver='lbfgs', random_state=1, max_iter=10000))
#
# Create the parameter grid
#
param_grid = [{
'logisticregression__C': [0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1.0, 10.0]
}]
#
# Create the Grid Search estimator instance for selecting model using
# 2-fold StratifiedKFold cross validation
#
gs = GridSearchCV(estimator=pipeline, param_grid = param_grid,
cv = 2, scoring = 'accuracy', n_jobs = 1, refit = True)
#
# Calculate the generalization error / accuracy
#
scores = cross_val_score(gs, X_train, y_train, scoring='accuracy', cv=5)
#
# Print the mean scores and standard deviation
#
print('CV accuracy: %.3f +/- %.3f' % (np.mean(scores), np.std(scores)))
Going by the above accuracy, one would want to select Logistic Regression algorithm for model. One can then apply 10-fold cross validation technique and use Grid search or randomized search for selecting the most optimal model.
Conclusions
Here is the summary of what you learned regarding the usage of nested cross-validation technique:
- In order to select the algorithm which can result in creation of most optimal model, one can use the nested cross validation technique.
- Nested cross validation technique represents the k-fold cross-validation in outer loop used for estimating the generalization accuracy of the model while k-fold cross-validation in inner loop for selection of best model with most optimal hyper parameters.
- One of the nested cross validation technique is 5×2 cross validation which represents the 5-fold cross validation outer loop for estimating the generalization accuracy while 2-fold cross validation inner loop for selection of the model.
- Nested cross-validation results in unbiased estimate of true error relative to the test data set.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com
- Linear Regression T-test: Formula, Example - May 7, 2024
- Feature Engineering in Machine Learning: Python Examples - May 3, 2024
- Feature Selection vs Feature Extraction: Machine Learning - May 2, 2024
Leave a Reply