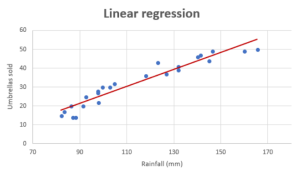
If you want to build a model for predicting a numerical value and wondering whether the linear regression model is most appropriate or valid, then creating the regression scatter plot is the most efficient way. And, this works best if the data set is two or three-dimensional. If a dataset is two-dimensional, it’s simple enough to plot the data to determine its shape. You can plot three-dimensional data too. The objective is to find whether the data set is relatively linear. When the plot is created, the data points fall roughly along a straight line as shown below.
Whether Linear Regression Appropriate for High-dimension Datasets?
The challenge comes when we come across multi-dimensional datasets. This resembles the real-world scenario. How do we determine whether the linear regression model can be the most appropriate model for a regression problem? The challenge happens because it is not possible to create a linear scatter plot to the assess data linear relationship for a dataset which is having more than three dimensions.
To determine whether a high-dimensional dataset might be suitable for linear regression, one effective approach is to reduce the dimensionality of the dataset to two or three dimensions and then visualize the results. This can be achieved using techniques like Principal Component Analysis (PCA) and t-distributed Stochastic Neighbor Embedding (t-SNE). Both reduce the dimensionality of a dataset without incurring much loss of information. With PCA, for example, it is found to reduce the number of dimensions by 90% while retaining 90% of the information in the original dataset.
The following is a high-level summary of above-mentioned techniques for dimensionality reduction:
Principal Component Analysis (PCA):
- PCA is a statistical technique that transforms the data into a new coordinate system. The new coordinates (called principal components) are linear combinations of the original variables.
- The first principal component captures the most variance in the data, the second captures the next most, and so on.
- A key feature of PCA is that it often allows a significant reduction in dimensionality with minimal loss of information. For example, you might reduce a dataset from 100 dimensions to just 10 while retaining 90% of the original information. This makes it possible to plot the data in 2D or 3D and observe potential linear relationships.
t-distributed Stochastic Neighbor Embedding (t-SNE):
- t-SNE is another dimensionality reduction technique, but it’s primarily used for visualization rather than for preserving linear relationships.
- t-SNE focuses on preserving the local structure of the data, meaning that similar data points in high-dimensional space will be close to each other in the reduced space.
- While t-SNE is excellent for visualizing complex structures and clusters, it doesn’t necessarily preserve linear relationships as PCA does. However, it can still give insight into the general structure and separability of the data.
This is how the dimensionality reduction technique helps in deciding appropriateness of linear regression model for high-dimensional datasets:
- After reducing the dataset’s dimensionality, if you observe that the data points form a linear pattern or clusters that could be separated linearly, it suggests that the high-dimensional dataset might be well-suited for linear regression.
- Conversely, if no clear linear relationships are observed in the reduced dimensions, it might indicate that a linear model may not capture the complexity of the data, and you might need to consider more complex models.
The process of dimensionality reduction might seem like it magically simplifies data, but it is grounded in mathematical principles. PCA, for example, relies on eigenvalue decomposition or singular value decomposition to find the directions (principal components) that capture the most variance in the data. This is why PCA can significantly reduce dimensions while retaining most of the information.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me