Last updated: 10th Aug, 2024
Lasso regression, sometimes referred to as L1 regularization, is a technique in linear regression that incorporates regularization to curb overfitting and enhance the performance of machine learning models. It works by adding a penalty term to the cost function that encourages the model to select only the most important features and set the coefficients of less important features to zero. This makes Lasso regression a popular method for feature selection and high-dimensional data analysis.
In this post, you will learn concepts, formulas, advantages, and limitations of Lasso regression along with Python Sklearn examples. The other two similar forms of regularized linear regression are Ridge regression and Elasticnet regression.
What’s Lasso Regression?
Lasso regression algorithm is a machine learning algorithm that can be used to perform linear regression while also reducing the number of features used in the model. Lasso stands for least absolute shrinkage and selection operator. Pay attention to the words, “least absolute shrinkage” and “selection”.
- Least absolute shrinkage refers to the way Lasso regression minimizes the sum of the absolute values of the coefficients in the regression model. Lasso modifies this by adding a penalty term to the minimization. This penalty is proportional to the absolute value of the coefficients (hence “absolute shrinkage”). This method is called as L1 regularization. This is why Lasso regression is also called L1-norm regularization.
- The “selection” aspect of Lasso comes from this property of pushing coefficients to zero. In practical terms, if a coefficient is zero, it means that the corresponding variable is effectively excluded from the model. In this manner, Lasso automatically performs feature selection by retaining only those variables in the model that have a significant impact on the output, discarding the others
Limitations of Lasso Regression
Lasso regression is often used precisely because it is effective in scenarios where the number of features is large, possibly even larger than the number of samples. This is due to its ability to perform feature selection by setting some coefficients to zero. However, the limitation of Lasso regression in scenarios with a large number of features is not that it performs poorly, but rather that it can select at most n features before it saturates, where n is the number of samples. If there are more features than samples, Lasso might not be able to include all potentially relevant predictors in the model. Additionally, when variables are highly correlated, Lasso tends to arbitrarily select one of them and shrink the others to zero, which might not always be ideal depending on the context of the data.
Other limitation of lasso regression is problematic aspect of feature elimination. While Lasso’s ability to reduce the coefficients of some variables to zero is often beneficial for feature selection and model simplicity, it can indeed be problematic if it incorrectly eliminates relevant features. This might happen if the model is not properly regularized or if the data is not preprocessed correctly.
How does Lasso Regression work?
Lasso regression is an extension of linear regression in the manner that a regularization parameter multiplied by the summation of the absolute value of weights gets added to the loss function (ordinary least squares) of linear regression. Lasso regression is also called regularized linear regression. The idea is to induce the penalty against complexity by adding the regularization term such that with increasing value of the regularization parameter, the weights get reduced (and, hence penalty induced) to keep the overall goal of the minimized sum of squares. The hypothesis or the mathematical model (equation) for Lasso regression is the same as linear regression and can be expressed as the following. However, what is different is loss function.
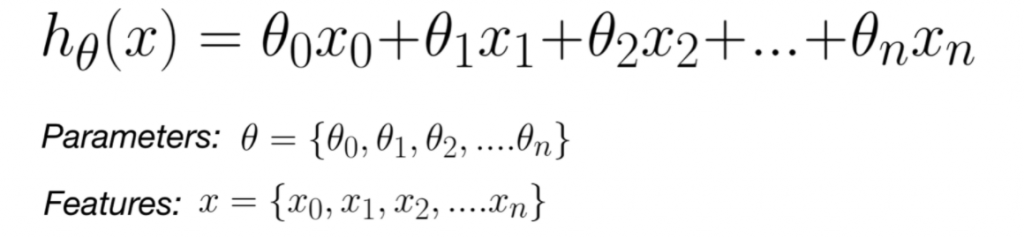
Here is the loss function of LASSO regression. Compare it with the loss function of linear regression.
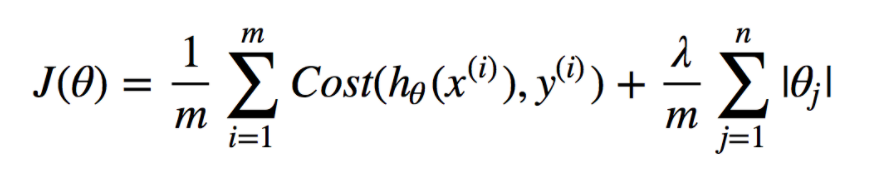
Compare it with the linear regression loss function.
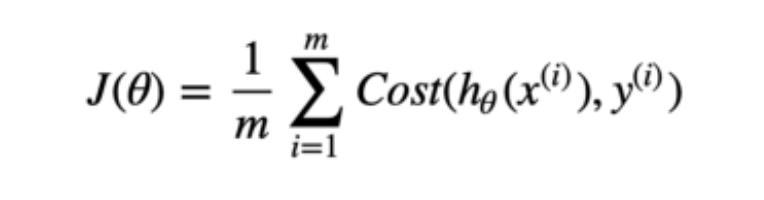
You may note that in Lasso regression’s loss function, there is an extra element such as the following:
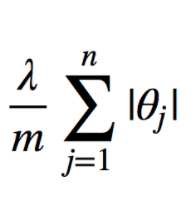
The equation in fig 4 represents the regularization parameter $\lambda$ and summation of absolute values of weights. “m” represents the constant. The increasing value of the regularization parameter means increasing regularization strength, the absolute values of weights would need to decrease (shrink) to keep the overall value of the loss function minimized. The optimization of the Lasso loss function results in some of the weights becoming zero and hence can be seen as a method of selection of the features. Pay attention to the usage of words, shrinkage, selection, and absolute. This is why LASSO is termed as Least absolute shrinkage and selection operator.
Optimizing the LASSO loss function does result in some of the weights becoming zero. Thus, some of the features will be removed as a result. This is why LASSO regression is considered to be useful as a supervised feature selection technique.
When to use Lasso Regression?
When there is a likelihood of a large number of outliers in the dataset, it is advised to use either Lasso or Ridge regression. Lasso regression mitigates the effect of outliers by lessening their influence on the outcome as coefficients are adjusted during training. Lasso regression has a secondary benefit too. If the training data suffers from multi-collinearity, a condition in which two or more input variables are linearly correlated so that one can be predicted from another with a reasonable degree of accuracy, Lasso effectively ignores the redundant data.
A classic example of multicollinearity occurs when a dataset includes one column specifying the number of rooms in a house and another column specifying the square footage. More rooms generally means more area, so the two variables are correlated to some degree.
Lasso Regression Python Example
In Python, Lasso regression models can be trained using the Lasso class from the sklearn.linear_model library. The Lasso class takes in a parameter called alpha which represents the strength of the regularization term. A higher alpha value results in a stronger penalty, and therefore fewer features being used in the model. In other words, a higher alpha value such as 1.0 results in more features being removed from the model than a value such as 0.1. The Lasso class also has a fit() method that can be used to fit the model to training data, and a predict() method that can be used to make predictions on new data.
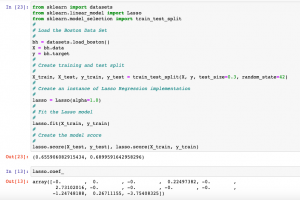
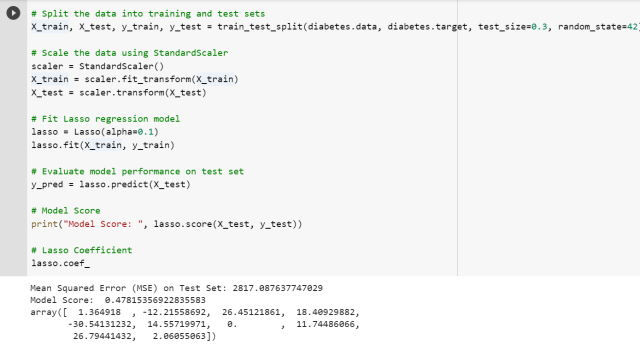
Here is the Python code which can be used for fitting a model using LASSO regression. Pay attention to some of the following in the code given below:
- Sklearn Breast Cancer dataset is used for training Lasso regression model
- Sklearn.linear_model Lasso class is used as Lasso regression implementation. The value of the regularization parameter is passed as 0.1
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
# Load the diabetes dataset
diabetes = datasets.load_diabetes()
# Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, test_size=0.3, random_state=42)
# Scale the data using StandardScaler
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# Fit Lasso regression model
lasso = Lasso(alpha=0.1)
lasso.fit(X_train, y_train)
# Evaluate model performance on test set
y_pred = lasso.predict(X_test)
# Model Score
print("Model Score: ", lasso.score(X_test, y_test))
# Lasso Coefficient
lasso.coef_
Once the model is fit, one can look into the coefficients by printing lasso.coef_ command. It will be interesting to find that some of the coefficients value is found to be zero. Here is the screenshot:
Lasso Regression Cross-validation Python Example
In this section, you will see how you could use the cross-validation technique with Lasso regression. Pay attention to some of the following:
- Sklearn.linear_model LassoCV is used as Lasso regression cross validation implementation.
- LassoCV takes one of the parameter inputs as “cv” which represents a number of folds to be considered while applying cross-validation. In the example below, the value of cv is set to 5.
- Also, the entire dataset is used for training and testing purposes. This is unlike the 2-way or 3-way holdout method where the model is trained and tested on different data split.
- The model performance of the LassoCV model is found to be greater than the Lasso regression algorithm.
from sklearn import datasets
from sklearn.linear_model import LassoCV
from sklearn.model_selection import train_test_split
#
# Load the Boston Data Set
#
bh = datasets.load_boston()
X = bh.data
y = bh.target
#
# Create an instance of Lasso Regression implementation
#
lasso_cv = LassoCV(cv=5)
#
# Fit the Lasso model
#
lasso_cv.fit(X, y)
#
# Create the model score
#
lasso_cv.score(X, y)
The following code can be used for fine tuning Lasso regularization parameter using Grid search. The code given below has used the GridSearchCV function from scikit-learn, which allows us to search over a range of parameter values and select the best combination based on cross-validation performance.
from sklearn.model_selection import GridSearchCV
# Define parameter grid
param_grid = {'alpha': [0.001, 0.01, 0.1, 1, 10]}
# Perform grid search with cross-validation
lasso_cv = GridSearchCV(Lasso(), param_grid, cv=5)
lasso_cv.fit(X_train, y_train)
# Print best parameter values and score
print("Best Parameters:", lasso_cv.best_params_)
print("Best Score:", lasso_cv.best_score_)
Conclusions
Here is the summary of what you learned in relation to LASSO regression:
- Lasso regression extends Linear regression in the way that a regularization element is added to the least-squares loss function of linear regression in order to induce the penalty (decrease weights) against complexity (large number of features)
- Increasing regularization parameter value (strength) results in weights getting reduced. This may result in some of the weights becoming zero. This is why Lasso regression is also considered for supervised feature selection.
- Use LassoCV implementation for applying cross-validation to Lasso regression.
- A higher alpha value results in a stronger penalty, and therefore fewer features being used in the model. In other words, a higher alpha value such as 1.0 results in more features being removed from the model than a value such as 0.1.
- Mathematics Topics for Machine Learning Beginners - July 6, 2025
- Questions to Ask When Thinking Like a Product Leader - July 3, 2025
- Three Approaches to Creating AI Agents: Code Examples - June 27, 2025
I found it very helpful. However the differences are not too understandable for me