Last updated: 25th Nov, 2023
Bagging is a type of an ensemble machine learning approach that combines the outputs from many learner to improve performance. The bagging algorithm works by dividing the training set into smaller subsets. These subsets are then processed through different machine-learning models. After processing, the predictions from each model are combined. This combination of predictions is used to generate an overall prediction for each instance in the original data. In this blog post, you will learn about the concept of Bagging along with Bagging Classifier Python code example.
Bagging can be used in machine learning for both classification and regression problem. The bagging classifier technique is utilized across a range of machine learning algorithms. These include decision stumps, artificial neural networks (such as multi-layer perceptron), support vector machines, and maximum entropy classifiers.
Check out my detailed post on machine learning titled What is machine learning? Concepts & Examples. It does provide different definitions along with explaining different aspects of machine learning which will be useful for creating good concepts around machine learning. Here is the sample excerpt:
Machine learning is about approximating mathematical functions (equations) representing real-world scenarios. These mathematical functions are also referred to as “mathematical models” or just models. The reason why machine learning models are called function approximations because it will be extremely difficult to find exact function which can be used to predict or estimate real world scenarios.
Introduction to Bagging Classifier
A bagging classifier, in the context of classification, is an ensemble model formed by training multiple versions of a basic model / base estimator on various iterations of the training data set. This data set is modified using a bagging sampling technique, where data is sampled with replacement, or through other methods. Each version of the basic model learns from a slightly different set of data, contributing to a more robust overall classification model. The bagging sampling technique can result in a training set consisting of a duplicate dataset or a unique data set. This sampling technique is also called bootstrap aggregation. The final predictor (also called a bagging classifier) combines the predictions made by each estimator/classifier by voting (classification) or by averaging (regression). Read more details about this technique in this paper, Bias, Variance and Arcing Classifiers by Leo Breiman.
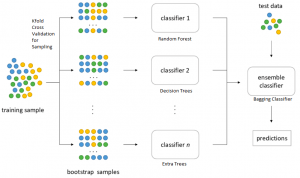
While creating each of the individual models, one can configure the number of samples and/or features that need to be considered while fitting the individual estimators. Take a look at the diagram below to get a better understanding of the bagging classification.
The basic idea is to repeatedly (with replacement) sample observations from the training set and use each observation as a “bootstrap sample” in fitting different estimators that will be combined in the final result. Pay attention to some of the following in the above diagram:
- Training data sets consists of data samples represented using different colors.
- Random samples are drawn with replacement. This essentially means that there could be duplicate data in each of the samples.
- Each sample is used to train different classifiers represented using classifier 1, classifier 2, …, classifier n
- An ensemble classifier is created which takes the predictions from different classifiers and make the final prediction based on voting or averaging respectively.
- The performance of the ensemble classifier is tested using the training data set.
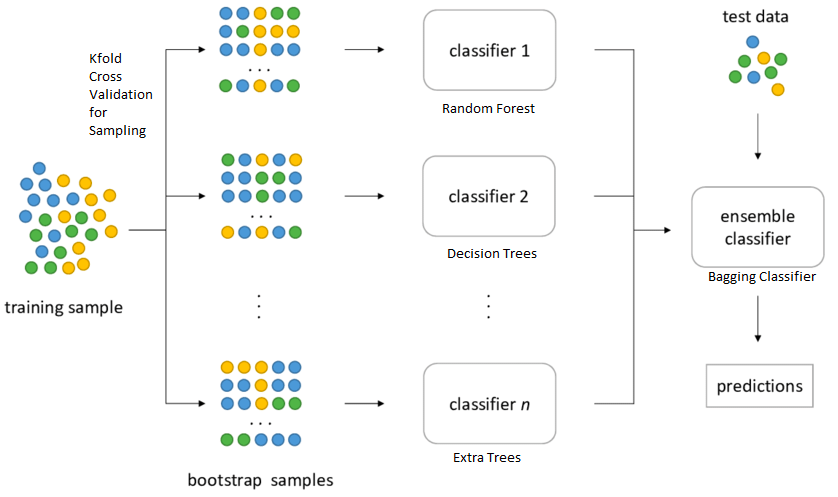
Here is another view of the bagging classifier. Note how different bags of training data set is created with replacement. Different bags may represent data related to different features which can be used to train different models.
# Why / When to use bagging classifier
The following are some of the reasons for using bagging classifiers:
- Reduces Overfitting: Bagging is particularly effective in reducing overfitting, which is a common problem in machine learning models. By training on various subsets of the data and then aggregating the results, the bagging classifier creates a more generalized model.
- Improves Stability: The method enhances the stability of the machine learning models. Even if a part of the data is noisy, the overall model remains unaffected because of the averaging or voting process.
- Handles High Variance: It is especially beneficial for algorithms that have high variance. The averaging of predictions across various models reduces this variance, leading to more reliable predictions. You may want to check this post to get a better understanding of Bias and Variance concepts – Bias & variance concepts and interview questions
- Parallelizable Computation: The training of individual models in a bagging classifier can be done in parallel, which speeds up the training process. This is particularly useful for large datasets.
- Improves Accuracy: By combining the strengths of multiple models, bagging often leads to an improvement in prediction accuracy compared to individual models.
- Robust to Outliers: Since bagging involves training on different subsets of data, the overall model is less sensitive to outliers than individual models might be.
# Sampling techniques for bagging
Bagging Classifier can be termed as some of the following based on the sampling technique used for creating training samples:
- Pasting Sampling: When the random subsets of data is taken in the random manner without replacement (bootstrap = False), the algorithm can be called as Pasting
- Bagging Sampling: When the random subsets of data are drawn with replacement (bootstrap = True), the algorithm can be called as Bagging. It is also called as bootstrap aggregation.
- Random Subspace: When the random subsets of features are drawn, the algorithm can be termed as Random Subspace.
- Random Patches: When both the ransom subsets of samples and features are drawn, the algorithm can be termed as Random Patches.
In this post, the bagging classifier is created using Sklearn BaggingClassifier with a number of estimators set to 100, max_features set to 10, and max_samples set to 100 and the sampling technique used is the default (bagging). The method applied is random patches as both the samples and features are drawn in a random manner.
Bagging Classifier Python Example
In this section, you will learn about how to use Python Sklearn BaggingClassifier for fitting the model using the Bagging algorithm. The following is done to illustrate how the Bagging Classifier help improves the generalization performance of the model. In order to demonstrate the aspects of generalization performance, the following is done:
- A model is fit using LogisticRegression algorithm
- A model is fit using BaggingClassifier with base estimator as LogisticRegression
The Sklearn breast cancer dataset is used for fitting the model.
Model fit using Logistic Regression
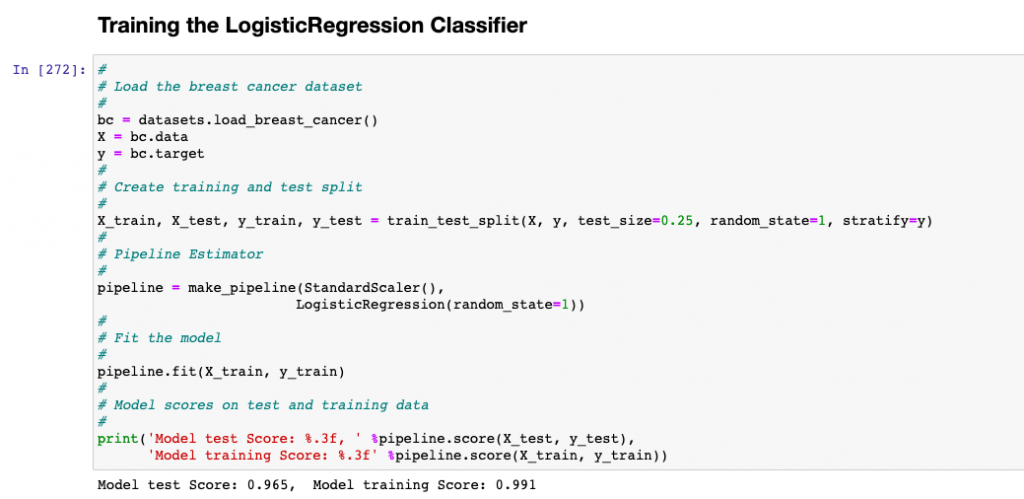
Here is the code which can be used to fit a logistic regression model:
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.ensemble import BaggingClassifier
from sklearn.model_selection import GridSearchCV
#
# Load the breast cancer dataset
#
bc = datasets.load_breast_cancer()
X = bc.data
y = bc.target
#
# Create training and test split
#
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=1, stratify=y)
#
# Pipeline Estimator
#
pipeline = make_pipeline(StandardScaler(),
LogisticRegression(random_state=1))
#
# Fit the model
#
pipeline.fit(X_train, y_train)
#
# Model scores on test and training data
#
print('Model test Score: %.3f, ' %pipeline.score(X_test, y_test),
'Model training Score: %.3f' %pipeline.score(X_train, y_train))
The model comes up with the following scores. Note that the model tends to overfit the data as the test score is 0.965 and the training score is 0.991.
Model fit using Bagging Classifier
In this section, we will fit a bagging classifier using different hyperparameters such as the following and base estimator as pipeline built using Logistic Regression. Note that you can further perform a Grid Search or Randomized search to get the most appropriate estimator.
- n_estimators = 100
- max_features = 10
- max_samples = 100
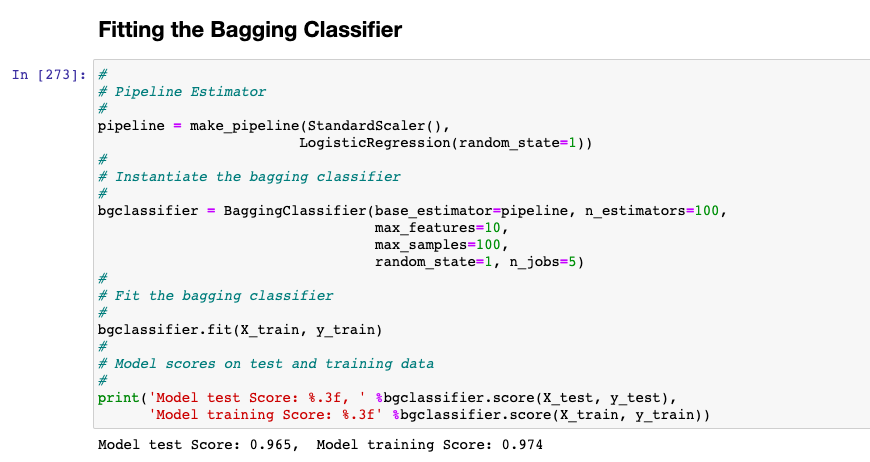
Here is how the Python code will look like for the Bagging Classifier model:
#
# Pipeline Estimator
#
pipeline = make_pipeline(StandardScaler(),
LogisticRegression(random_state=1))
#
# Instantiate the bagging classifier
#
bgclassifier = BaggingClassifier(base_estimator=pipeline, n_estimators=100,
max_features=10,
max_samples=100,
random_state=1, n_jobs=5)
#
# Fit the bagging classifier
#
bgclassifier.fit(X_train, y_train)
#
# Model scores on test and training data
#
print('Model test Score: %.3f, ' %bgclassifier.score(X_test, y_test),
'Model training Score: %.3f' %bgclassifier.score(X_train, y_train))
The model comes up with the following scores. Note that the model tends to overfit the data as the test score is 0.965 and the training score is 0.974. However, the model will give better generalization performance than the model fit with Logistic Regression.
Conclusions
Here is the summary of what you learned about the bagging classifier and how to go about training / fitting a bagging classifier model:
- Bagging classifier is an ensemble classifier which is created using multiple estimators which can be trained using different sampling techniques including pasting (samples drawn without sampling), bagging or bootstrap aggregation (samples drawn with replacement), random subspaces (random features are drawn), random patches (random samples & features are drawn)
- Bagging classifier helps reduce the variance of individual estimators by sampling technique and combining the predictions.
- Consider using bagging classifier for algorithm which results in unstable classifiers (classifier having high variance). For example, decision tree results in construction of unstable classifier having high variance and low bias.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me