Activation Functions in Neural Networks: Concepts, Examples

Last updated: 24th Nov, 2023

The activation functions are critical to understanding neural networks. There are many activation functions available for data scientists to choose from, when training neural networks. So, it can be difficult to choose which activation function will work best for their needs. In this blog post, we look at different activation functions and provide examples of when they should be used in different types of neural networks. If you are starting on deep learning and wanted to know about different types of activation functions, you may want to bookmark this page for quicker access in the future.

What are activation functions in neural networks?

In a neural network, an activation function is a mathematical function that determines whether a particular input should be activated or not. In other words, it decides whether a neuron should fire and send a signal to the next layer in the network.

Understanding activation function through an analogy of neuron functioning in our brain

In reality, the way activation works in the brain can be visualized through an analogy:

Think of a neuron in the brain as a gatekeeper in a medieval castle. This gatekeeper, representing the neuron, is responsible for deciding whether to pass a message to the next gatekeeper (another neuron). This decision is not arbitrary but is governed by a set of complex and precise rules.

In the brain, these rules are dictated by a combination of biochemical reactions and electrical signals. When a neuron receives signals from other neurons, these signals are in the form of neurotransmitters – chemical messengers that bridge the gap (synapse) between neurons. The neuron, like our gatekeeper, assesses these signals.

If the sum of these incoming signals is strong enough to surpass a certain threshold, the neuron becomes ‘activated’. This is akin to the gatekeeper deciding the message is important enough to be passed on. When activated, the neuron then fires its own signal down its axon, towards other neurons, continuing the chain of communication. This firing is an electrical impulse, a rapid change in voltage across the neuron’s membrane.

Understanding the role of activation functions in neural networks

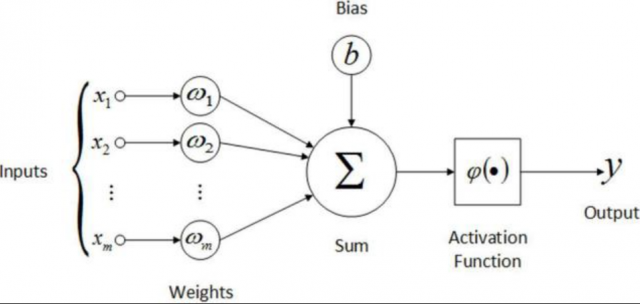
The picture below illustrates the structure of a single neuron within a neural network and highlights the role of the activation function.

• These are the data points (x1​,x2​,…,xm​) that the neuron receives. Each input is associated with a weight (ω1​,ω2​,…,ωm​), which represents the strength or importance of that input in the neuron’s decision-making process.
• The weights ($\omega$) are the parameters that the neural network adjusts during the training process. They scale the inputs and determine how much influence each one has on the neuron’s output.
• The neuron calculates a weighted sum of the inputs and the bias. This is done by multiplying each input by its corresponding weight and adding them all together.
• The activation function is applied to the weighted sum plus the bias. Its role is to introduce non-linearity into the network, enabling it to learn and model complex relationships between the inputs and outputs. Without non-linearity, the network would only be able to model linear relationships, which would be a significant limitation.
• The result of the activation function is the neuron’s output, which then becomes the input to the next layer in the network, or the final output of the network if this is the output layer.

There are many different activation functions that can be used, and the choice of activation function can have a significant impact on the performance of the neural network. The most common activation functions used in a neural network are the sigmoid function, the Tanh function, and the ReLU function. Each activation function has its own advantages and disadvantages which will be explained later in this post. In general, activation functions are chosen based on the specific problem that needs to be solved.

Different types of activation functions in neural networks

Without further ado, let’s take a look at the animation which represents different types of activation functions:

Here is the list of different types of activation functions shown in the above animation:

• Identity function (Used in Adaline – Adaptive Linear Neuron): The identity function is a special case of an activation function where the output signal is equal to the input signal. In other words, the identity function simply passes the input signal through unchanged. While this might not seem very exciting, it turns out that the identity function can be very useful in certain situations. For example, if you want your neural network to output a continuous signal instead of a discrete one, then using the identity function as your activation function can help to achieve this. The identity function on a given set is often denoted by the identity matrix.
  
  If f is an identity function on a set X, then we usually write f(x) = x for all x in X. The following plot represents the identity function.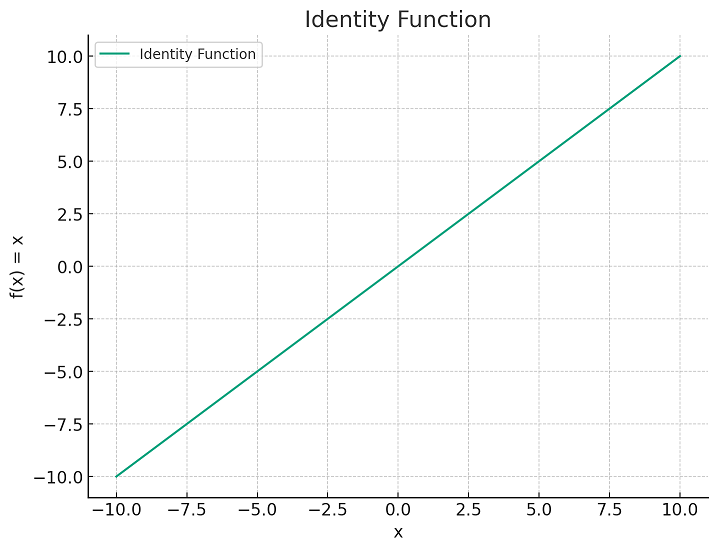
  
  
  
• Sigmoid function: The Sigmoid function takes the number between 0 and (positive) infinity as input and transforms it into an output between 0 and 1. It is also called as squashing function. The following is the formula of sigmoid function.
  
  $\sigma(x) = \frac{1}{1 + e^{-x}}$
  
  The output can be interpreted as a probability, which makes it useful for classification tasks. As the Sigmoid function is also differentiable, it can be used to train a neural network. It is one of the most common activation functions used for neural networks. This function results in smooth and monotonic activation curves. The Sigmoid function is used in many types of neural networks, including feedforward neural networks. The following plot represents the output of the sigmoid function vs input: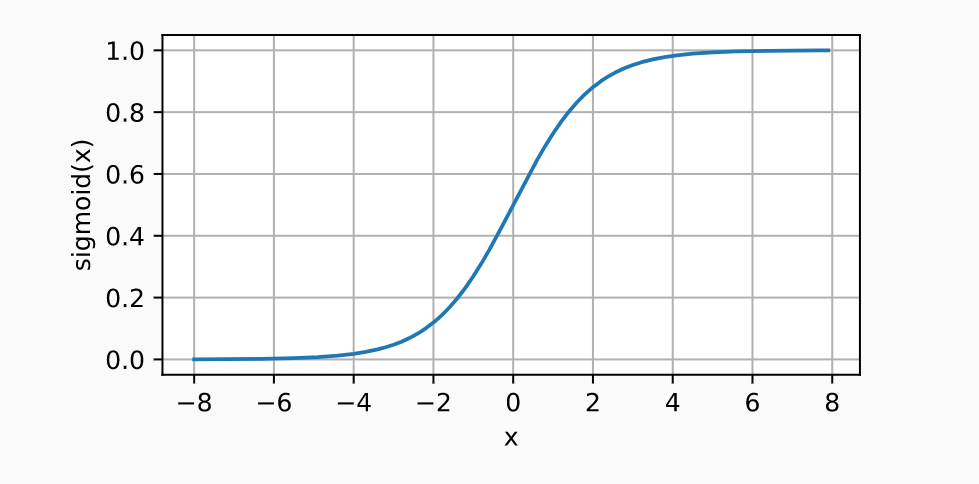
  
  
  
• Tanh function: The Tanh function is often used as an activation function in neural networks. It is a nonlinear function that squashes a real-valued number to the range [-1, 1]. The following is the formula of tanh function:
  
  $\tanh(x) = \frac{e^{x} – e^{-x}}{e^{x} + e^{-x}}$
  
  Tanh is continuous, smooth, and differentiable. It has an output range that is symmetric about 0, which helps preserve zero Equivariance during training. The function outputs values close to -1 or 1 when the input is large in magnitude (positive or negative). This means that the gradient at these output values remains close to 1, which aids in training deep neural networks (where gradients often get smaller as backpropagation progresses). Tanh can also be thought of as a rescaled version of the sigmoid function. The following plot represents the output of the Tanh function vs input: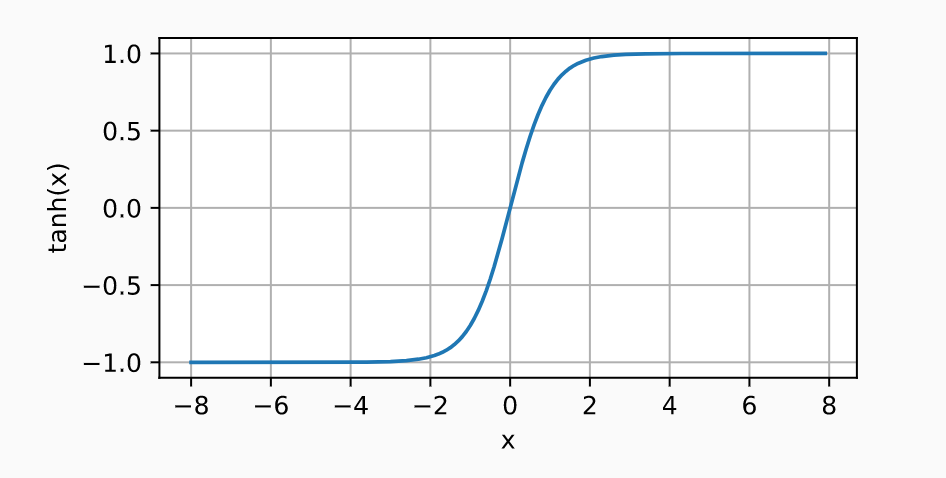
  
  
  
• Softmax function: The Softmax function is a type of activation function that is often used in neural networks. It squashes the output of each unit in the network so that it is between 0 and 1, and so that the sum of all the outputs is 1. This makes it ideal for use in classification tasks, where each unit corresponds to a class and we want to be able to say with certainty which class the input belongs to. Softmax functions are often used in the output layer of neural networks, where they compute the probabilities for each class. The following is the formula of softmax function:
  
  $\sigma(\mathbf{z})i = \frac{e^{z_i}}{\sum{j=1}^{K} e^{z_j}}$
  
  Here, (σ(z)i​ represents the i-th component of the output vector of the softmax function, ezi​ is the exponential of the i-th element of the input vector z, and the denominator is the sum of the exponentials of all K elements in z. This formulation ensures that the softmax function outputs a probability distribution over K classes.
  
• ArcTan function (inverse tangent function): ArcTan is a trigonometric function that is commonly used as an activation function in neural networks. ArcTan takes a real number as an input and returns a real number between -π/2 and π/2. ArcTan is continuous and differentiable, which makes it well-suited for use in neural networks. The ArcTan function has a range of benefits, including its ability to prevent neurons from saturating, its computational efficiency, and its robustness against noise. Overall, the ArcTan function is a powerful activation function that can be used to improve the performance of neural networks.
  
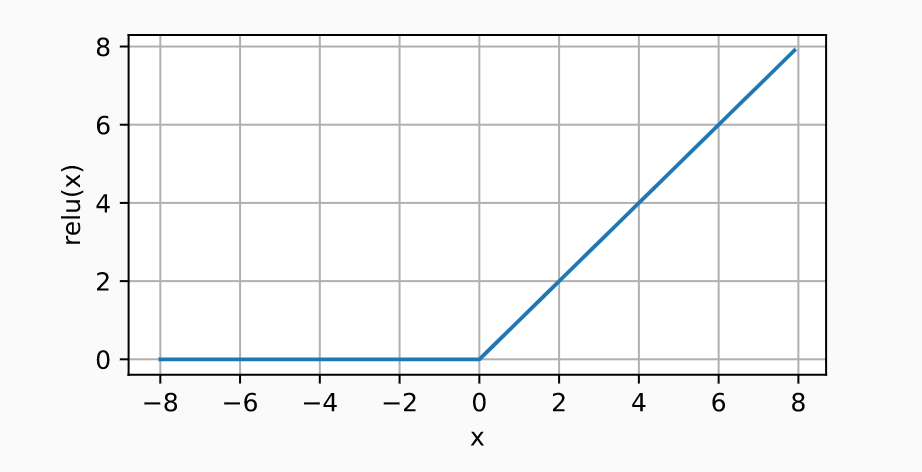
• ReLU (Rectified Linear Unit): ReLU is a type of activation function that is used in neural networks. ReLU stands for Rectified Linear Unit. ReLU is a linear function that returns the input if it is positive, and returns zero if it is negative. ReLU is a piecewise linear function. ReLU has a range of [0, infinity]. ReLU is defined as: f(x) = max(0, x). ReLU is not differentiable at zero, which can be problematic for some optimization algorithms. ReLU is the most commonly used activation function because it is computationally efficient and has fewer issues with vanishing gradients than other activation functions. ReLU has been shown to outperform other activation functions in deep learning applications. ReLU is generally used in the hidden layers of a neural network. It is used in feed-forward neural networks to produce smooth nonlinear activation. It is also used in convolutional neural networks that have linear receptive fields and a large output layer with several neurons. It is different from the sigmoid activation function in the sense that it is easier to train and results in faster convergence. The following plot represents the output of the ReLU function vs input:
  
  
  
• Leaky ReLU (Improved version of ReLU): Leaky ReLU function is an activation function that is mostly used in the case of activation function for neural networks. It was introduced by Cagnin et al. (2012). Unlike traditional ReLU functions, which set all negative values to zero, Leaky ReLU allows a small amount of negative values to pass through. This has the effect of reducing the “dying” ReLU problem, where neurons can become permanently deactivated if they receive too many negative inputs. Leaky ReLU is therefore seen as a more robust activation function, and it has been shown to improve the performance of neural networks in various tasks.
  
• Randomized ReLU: The Randomised ReLU function is a generalization of the standard ReLU function and can be used in place of the ReLU function in any neural network. The Randomised ReLU function has been shown to outperform the standard ReLU function in terms of both training time and classification accuracy. Moreover, the Randomised ReLU function is also more robust to input noise than the standard ReLU function.
  
• Parametric ReLU: Parametric ReLU function is a rectified linear unit (ReLU) with parameterized slope α. The Parametric ReLU function is given by: f(x)=max(0,x)+αmin(0,x). The standard ReLU function is given by: f(x)=max(0,x). The Parametric ReLU function was proposed by He et al. in their 2015 paper “Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”. In the paper, the authors found that the Parametric ReLU function improved the performance of deep neural networks on image classification tasks. The Parametric ReLU function has also been found to improve the training of deep neural networks and to reduce the number of parameters required to achieve a given performance level. This activation function is used in many modern deep learning architectures such as ResNet, DenseNet, and Alexnet which have enabled us to work on large-scale datasets.
  
• Exponential ReLU: The Exponential ReLU function is an activation function that has been shown to produce better results than the traditional ReLU function in several deep learning tasks. The Exponential ReLU function is defined as: f(x) = exp(x) if x<0, x if x>=0. The Exponential ReLU function has two primary advantages over the traditional ReLU function. First, the Exponential ReLU function avoids the “dying ReLU” problem, which occurs when a traditional ReLU-activated neuron outputs a negative value and is then unable to recover. Second, the Exponential ReLU function allows for a greater range of activity levels, which can lead to improved performance on some tasks. Despite these advantages, the Exponential ReLU function does have one significant disadvantage: it is much more computationally expensive than the traditional ReLU function. For this reason, it is important to carefully consider whether the Exponential ReLU function is the best choice for a given task before implementing it in a neural network.
  
• Soft Sign: Soft Sign is a mathematical function that is used in various fields such as machine learning and statistics. The Soft Sign function is defined as: Softsign(x) = x / (1 + |x|). This function has a number of useful properties, which make it well suited for use as an activation function in a neural network. Firstly, the Soft Sign function is continuous and differentiable, which is important for the training of a neural network. Secondly, the Soft Sign function has a range of (-1, 1), which means that it can be used to model bipolar data. Finally, the Soft Sign function is computationally efficient, which is important for large-scale neural networks. A common use of the soft sign activation function is when we learn using maximum likelihood estimation (MLE). In MLE, we try to find the activation function that best fits our training data. There are many different activation functions, but most of them result in a similar model when used with MLE. The soft sign activation function is also commonly used for classification problems where we want to learn probability estimates (Pr(y = +)) or Pr(y = -)). You can use soft sign activation functions in neural networks with binary output units where we want to learn the probabilities for each possible outcome.
  
• Inverse Square Root Unit (ISRU): In mathematics, the inverse square root function is defined as the function that is equal to the reciprocal of the square root of its argument. In other words, if x is any nonzero real number, then ISRU (x) = 1/sqrt(x). ISRU is a monotonic function and has a range of (-inf, inf). It is continuous and differentiable. The Inverse Square Root Unit function has several desirable properties that make it well-suited for use as an activation function in neural networks. In particular, the function is smooth, which helps to ensure that the neural network will converge to a solution. Additionally, the function is bounded, which helps to prevent the weights from becoming too large.
  
• Square Non-linearity: The Square Non-linearity function is a common activation function used in neural networks. This function takes the input, x, and outputs the square of x, f(x)=x^2. This function is non-linear, meaning that it can create complex models that are not linearly separable. The Square Non-linearity function is also differentiable, making it easier to train the neural network.
  
• Bipolar ReLU: Bipolar Rectified Linear Unit (BReLU) function is a type of activation function that is used in neural networks. It is similar to the standard ReLU function, except that it has a range of -1 to 1 instead of 0 to 1. Its popularity stems from its ability to train deep neural networks quickly and effectively. The Bipolar ReLU function is very similar to the traditional ReLU function, but with one key difference. Whereas the traditional ReLU function returns 0 for any input below 0, the Bipolar ReLU function returns -1 for any input below 0. This seemingly small change can have a big impact on training time and accuracy. The Bipolar ReLU function has been shown to provide a more consistent gradient, which leads to faster training times. In addition, the Bipolar ReLU function often provides better generalization than the traditional ReLU function. Bipolar ReLU has been shown to outperform standard ReLU in some applications. It is also less prone to the “dying ReLU” problem, where neurons with a negative input become inactive and stop learning.
  
• Soft Plus: Soft Plus is a function that is often used as an activation function in neural networks. The function takes the form of f(x)=ln(1+e^x). The Soft Plus function has several desirable properties, including being differentiable, bounded, and monotonic. These properties make Soft Plus a good choice for use as an activation function in a neural network.

The following represents different variants of ReLU:

• Leaky ReLU
• Randomized ReLU
• Parametric ReLU
• Exponential linear unit
• Bipolar ReLU

Out of the above activation functions, the most commonly / popularly used are the following:

• Sigmoid
• Tanh
• ReLU and its different variants

• Author
• Recent Posts

Follow me

Ajitesh Kumar

I have been recently working in the area of Data analytics including Data Science and Machine Learning / Deep Learning. I am also passionate about different technologies including programming languages such as Java/JEE, Javascript, Python, R, Julia, etc, and technologies such as Blockchain, mobile computing, cloud-native technologies, application security, cloud computing platforms, big data, etc. For latest updates and blogs, follow us on Twitter. I would love to connect with you on Linkedin.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com

Follow me

Latest posts by Ajitesh Kumar (see all)

• GLM vs Linear Regression: Difference, Examples - December 7, 2023
• MinMaxScaler vs StandardScaler – Python Examples - December 7, 2023
• Linear Regression in Machine Learning: Examples - December 6, 2023