Have you ever wondered how regression models can be enhanced to provide more accurate predictions, even in the presence of outliers or data points with varying significance? Enter weighted regression machine learning models, an approach that assigns weights to data points, allowing for precise adjustments and improvements in prediction accuracy. In this blog post, we will learn about the concepts of weighted regression models with the help of examples while demonstrating with the help of Python implementation.
Traditional linear regression is a widely-used technique, but it may struggle when faced with outliers or situations where some data points carry more weight than others. However, weighted regression models help overcome these challenges. By assigning specific weights to each data point, the model becomes capable of capturing the nuances and complexities of the dataset, resulting in highly accurate predictions. But how exactly does this work? And how can we implement these models in Python?
In this blog, we will guide you through a step-by-step Python example using the scikit-learn library. From data preprocessing to weight assignment, model training, and prediction, we will uncover the greater details of weighted regression models. By comparing the outcomes with those of traditional linear regression, we will showcase the advantages and improvements offered by weighted regression.
What are weighted regression models?
Weighted Linear Regression is a variation of linear regression where each data point is assigned a weight that reflects its relative importance. This allows you to give more emphasis to certain data points and downplay the significance of others when fitting the regression line.
Weighted Linear Regression was developed to address the limitation of traditional linear regression when dealing with datasets where some data points are more important or have different degrees of influence than others. It allows us to assign weights to individual data points, reflecting their relative significance and adjusting their impact on the regression line accordingly.
To illustrate the need for weighted linear regression, let’s consider a real-world example. Suppose we want to build a model to predict housing prices based on features such as square footage, number of bedrooms, and location. We collect a dataset consisting of houses from different neighborhoods, and We want the model to be accurate across all neighborhoods.
However, it is noticed that certain neighborhoods have a higher variation in housing prices compared to others. For instance, houses in affluent neighborhoods tend to have a wider price range compared to houses in less desirable areas. In this case, using a traditional linear regression model without considering the variation in neighborhoods could result in a biased or inaccurate model.
Weighted linear regression comes into play here. By assigning weights to each data point, weighted regression models account for the varying importance or influence of different neighborhoods. Higher weights get assigned to data points from neighborhoods with larger price variations, indicating that these points should have a greater impact on the regression line. Conversely, data points from neighborhoods with smaller price variations can be assigned lower weights, indicating their relatively lesser influence on the model.
By using weighted linear regression, a model can be built that captures the nuances and variations across different neighborhoods, leading to more accurate predictions for each neighborhood and a more robust overall model.
Weighted Regression Model using Sklearn/Python
In this section, we will dive into a sample problem where we encounter a dataset with outliers. We’ll explore how a weighted regression model implemented in Python using the Sklearn library can help us handle these outliers and improve our predictive accuracy.
Imagine we have a dataset containing information about students’ hours of study and their corresponding test scores. However, there are a couple of outliers in the dataset, which are data points that deviate significantly from the overall pattern. These outliers may have been caused by measurement errors, unique circumstances, or other factors.
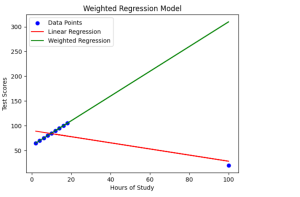
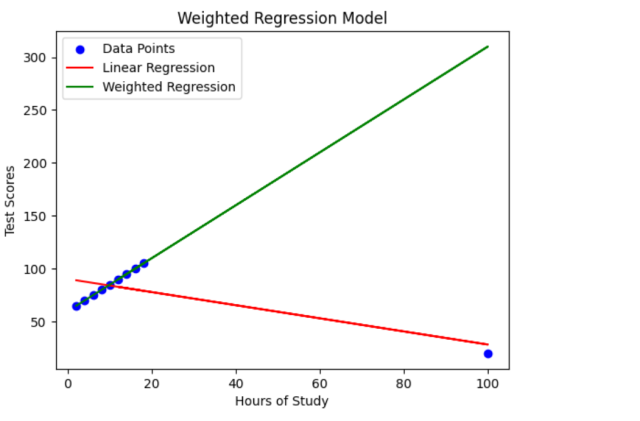
The goal is to build a regression model that can predict test scores based on the number of study hours. Since outliers can distort the regression line and impact the model’s accuracy, we will leverage a weighted regression approach to mitigate their influence and obtain more reliable predictions.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
# Set random seed for reproducibility
np.random.seed(42)
# Generate sample data with outliers
hours_of_study = np.array([2, 4, 6, 8, 10, 100, 12, 14, 16, 18]) # Study hours
test_scores = np.array([65, 70, 75, 80, 85, 20, 90, 95, 100, 105]) # Test scores
# Create a DataFrame
data = pd.DataFrame({'Hours_of_Study': hours_of_study, 'Test_Scores': test_scores})
# Split the data into input features (X) and target variable (y)
X = data[['Hours_of_Study']]
y = data['Test_Scores']
# Create a traditional linear regression model
linear_model = LinearRegression()
linear_model.fit(X, y)
# Create a weighted linear regression model
weights = np.ones_like(hours_of_study) # Initialize all weights as 1 (equal weights)
weights[5] = 0.1 # Assign lower weight to the outlier at index 5
weighted_model = LinearRegression()
weighted_model.fit(X, y, sample_weight=weights)
# Generate new data points for demonstration
new_hours_of_study = np.array([[5], [15]]) # New study hours for prediction
# Predict using the traditional linear regression model
y_pred_linear = linear_model.predict(new_hours_of_study)
# Predict using the weighted linear regression model
y_pred_weighted = weighted_model.predict(new_hours_of_study)
# Print the predictions
print("Predictions using linear regression:")
print(y_pred_linear)
print("\nPredictions using weighted linear regression:")
print(y_pred_weighted)
The following represents the explanation of the code:
- We start by importing the necessary libraries, including NumPy, Pandas, and Sklearn’s LinearRegression module.
- Next, a sample dataset is generated that consists of two NumPy arrays: hours_of_study representing the number of study hours, and test_scores representing the corresponding test scores.
- A DataFrame is created to store our sample data, with columns for hours of study and test scores.
- The dataset is split into input features X (hours of study) and the target variable y (test scores).
- A traditional linear regression model is trained using LinearRegression() and fit it to the data.
- For the weighted linear regression model, we initialize the weights with ones, indicating equal weights for all data points. We then assign a lower weight of 0.1 to the outlier at index 5, indicating its lesser influence on the model.
- We create the weighted linear regression model using LinearRegression() and fit it to the data, passing the sample_weight parameter to account for the assigned weights.
- To demonstrate the models’ predictions, we generate new data points (new_hours_of_study) representing study hours for which we want to predict the test scores.
- We make predictions using both the traditional linear regression model and the weighted linear regression model on the new data points.
The following picture demonstrates weighted regression model using scatter plot. Take a note of regression lines vis-a-vis impact of using weights.
Conclusion
A weighted regression model is an advanced approach that assigns different weights to data points based on their importance or precision. This allows for improved predictive accuracy and handling of outliers. Unlike traditional linear regression models that treat all data points equally, weighted regression models consider the varying significance of data points, leading to more accurate predictions and a better understanding of relationships between variables.
One example where a weighted regression model can be beneficial is in financial analysis. Outliers or extreme values can greatly impact financial analyses, but weighted regression models can assign appropriate weights to data points, mitigating the influence of outliers and providing more reliable predictions for making informed decisions. Sklearn, a popular Python library, offers the LinearRegression class for implementing weighted regression models. By specifying sample weights during model fitting, Sklearn enables easy integration of weighted regression into Python-based data analysis workflows, empowering analysts to extract meaningful insights from complex datasets with precision and efficiency.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me