Last updated: 7th Dec, 2023
Feature scaling is an essential part of exploratory data analysis (EDA), when working with machine learning models. Feature scaling helps to standardize the range of features and ensure that each feature (continuous variable) contributes equally to the analysis. Two popular feature scaling techniques used in Python are MinMaxScaler and StandardScaler.
In this blog, we will learn about the concepts and differences between these feature scaling techniques with the help of Python code examples, highlight their advantages and disadvantages, and provide guidance on when to use MinMaxScaler vs StandardScaler. Note that these are classes provided by sklearn.preprocessing module. As a data scientist, you will need to learn these concepts in order to train machine learning models using algorithms that require features to be on the same scale.
Differences between MinMaxScaler and StandardScaler
Both MinMaxScaler and StandardScaler scale the data (features), but they use different methods to achieve this. MinMaxScaler scales the data to a fixed range, typically between 0 and 1. On the other hand, StandardScaler rescales the data to have a mean of 0 and a standard deviation of 1. The following is the list of some of the key differences between StandardScaler and MinMaxScaler:
- Scaling Method:
- StandardScaler: Scales features by removing the mean and scaling to unit variance. This results in a transformation where the mean of the rescaled features becomes 0 with a standard deviation of 1.
- MinMaxScaler: Scales each feature by shrinking the range to a defined minimum and maximum, typically between 0 and 1. The transformation is based on the minimum and maximum values of each feature.
- Effect on Data Distribution:
- StandardScaler: Does not change the shape of the original distribution; it only standardizes the scale.
- MinMaxScaler: Can alter the shape of the original distribution, particularly if outliers are present.
- Sensitivity to Outliers:
- StandardScaler: Less sensitive to outliers since it focuses on standard deviation.
- MinMaxScaler: More sensitive to outliers because the scale is heavily influenced by the extreme maximum and minimum values.
- Resulting Data Characteristics:
- StandardScaler: Data transformed to have zero mean and unit variance, aligning with the assumptions of many machine learning algorithms.
- MinMaxScaler: Data transformed to fall within a specified range (e.g., 0 to 1), which can be beneficial for algorithms that require a bounded input space, like neural networks.
- Usage in Algorithms:
- StandardScaler: Preferred for algorithms that assume normally distributed data, such as linear models and Gaussian Naive Bayes.
- MinMaxScaler: Often used in algorithms that are sensitive to the scale of input data but do not assume any specific distribution, such as neural networks and distance-based algorithms like K-Nearest Neighbors.
- Handling Sparse Data:
- StandardScaler: May not be suitable for sparse data as it can break the sparsity.
- MinMaxScaler: Can be a better choice for sparse data, especially if preserving sparsity is important.
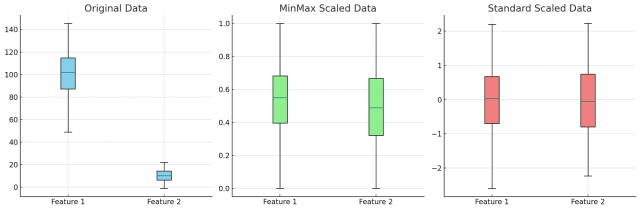
The following is a visual representation of application of Min Max Scaler and Standard Scaler.
Note some of the following in the above plot:
- The left most (Sky blue) plot shows the distribution of the two original features before any scaling is applied. The box plot for Feature 1 (left) indicates a higher median, larger interquartile range (IQR), and wider spread compared to Feature 2. This suggests that Feature 1 has a larger scale and variance. The box plot for Feature 2 (right) shows a lower median and a smaller IQR, indicative of a smaller scale and variance.
- In MinMax Scaled Data (Light Green Box Plot), after applying MinMaxScaler, both features are scaled to fall within the range of 0 to 1. The medians of both features are closer to the middle of the 0 to 1 range, and the IQRs are more comparable in size, illustrating that the features are now on a similar scale. The spread of the boxes is narrower, reflecting the compression of the data into the [0, 1] range.
- In Standard Scaled Data (Light Coral Box Plot), the StandardScaler transforms the data so that each feature has a mean of 0 and a standard deviation of 1. Both features show medians very close to 0 (the centerline of the plot), indicating that the mean has been centered. The IQRs and the overall range of the boxes are similar, suggesting that the features now have comparable variances.
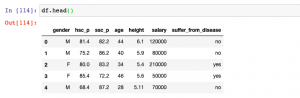
Here is the sample Pandas data frame which will be used later in this post for illustration of StandardScaler and MinMaxScaler:
import pandas as pd
import numpy as np
arr = np.array([['M', 81.4, 82.2, 44, 6.1, 120000, 'no'],
['M', 75.2, 86.2, 40, 5.9, 80000, 'no'],
['F', 80.0, 83.2, 34, 5.4, 210000, 'yes'],
['F', 85.4, 72.2, 46, 5.6, 50000, 'yes'],
['M', 68.4, 87.2, 28, 5.11, 70000, 'no']])
#
# Create Pandas DataFrame
#
df = pd.DataFrame(arr)
df.columns = ['gender', 'hsc_p', 'ssc_p', 'age', 'height', 'salary', 'suffer_from_disease']
#
# Convert the string data type to int and float appropriately
#
df[['age', 'salary']] = df[['age', 'salary']].astype(int)
df[['ssc_p', 'hsc_p', 'height']] = df[['ssc_p', 'hsc_p', 'height']].astype(float)
Here is how the data frame looks like:
Why is Feature Scaling needed?
Feature scaling is about transforming the values of different numerical features to fall within a similar range like each other. The feature scaling is used to prevent the supervised learning models from getting biased toward a specific range of values. For example, if your model is based on linear regression and you do not scale features, then some features may have a higher impact than others which will affect the performance of predictions by giving undue advantage for some variables over others. This puts certain classes at disadvantage while training model. This is why it becomes important to use scaling algorithms such as standard scaling or min max scaling.
This process of feature scaling is done so that all features can share the same scale and hence avoid problems such as some of the following:
- Loss in accuracy: Without feature scaling, features with larger numerical ranges can dominate the model’s learning process. This disproportionate influence skews the model’s attention towards these larger-scale features, potentially overlooking the contributions of smaller-scale features. For example, in the data set used in this post, pay attention to feature values of salary, age, and height. The values of salary are in the range of 50000 to 210000 (in the above example) while the values of age are in the range 1 to 100 and the values of height are in the range 4 ft to 7 ft. When such data set is applied on algorithms such as gradient descent optimization or K-nearest neighbors, the algorithm tries and find optimized weights or distances to handle feature values having larger values. This results in models which are sub-optimal in nature.
- Algorithm Performance: Many machine learning algorithms, especially those based on distance calculations like k-nearest neighbors (KNN) or gradient-based optimization techniques like in neural networks, perform better when features are on a similar scale. This is because large-scale features can disproportionately impact the model’s ability to learn.
- Prevention of Gradient Descent Issues: In models that use gradient descent for optimization (like linear regression, logistic regression, and neural networks), feature scaling helps in faster convergence. When features are on vastly different scales, the gradient descent can oscillate and take longer to find the minimum.
- Handling Outliers: Feature scaling, especially standardization, can help in mitigating the impact of outliers. However, it’s important to note that some methods like MinMaxScaler are sensitive to outliers.
- Enhanced computational cost: In algorithms that use optimization techniques, especially gradient descent, features with widely different scales can lead to inefficient convergence. The algorithm might require more iterations to find the optimal solution, as it struggles to balance the gradients across all features. This inefficiency directly translates into increased computational time and resource usage.
Scaling the data to a common range can help to alleviate this problem. In this case, we can use the MinMaxScaler or StandardScaler to scale the data so that the features such as the salary, age and income contribute equally to the analysis. By scaling the data, we can ensure that each feature has an equal impact on the model’s performance, and the model can make more accurate predictions.
Feature scaling is not important for algorithms such as random forest or decision trees which are scaling invariant. The scale of the value of the feature does not impact the model performance of models trained using these algorithms (random forest/decision tree).
Normalization vs Standardization
The two common approaches to bringing different features onto the same scale are normalization and standardization. Normalization (also called Min max Scaling) is implemented in Python using MinMaxScaler and the standardization (also known as Standard Scaling) is implemented using StandardScaler.
What is Normalization?
Normalization refers to the rescaling of the features to a range of [0, 1], which is a special case of min-max scaling. To normalize the data, the min-max scaling can be applied to one or more feature columns. Here is the formula for normalizing data based on min-max scaling. Normalization is useful when the data is needed in the bounded intervals.
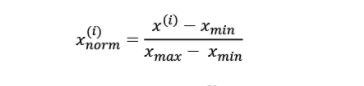
This is how the Python method would look like for normalizing one or more columns:
def normalize(values):
return (values - values.min())/(values.max() - values.min())
In order to apply the normalization technique to one or more feature columns, one could use the following Python code (with reference to the dataset used in this post). Note the usage of apply method which applies the normalize method shown above on multiple feature columns all at once.
cols = ['hsc_p', 'ssc_p', 'age', 'height', 'salary']
#
# Normalize the feature columns
#
df[cols] = df[cols].apply(normalize)
What is Standardization?
The standardization technique is used to center the feature columns at mean 0 with a standard deviation of 1 so that the feature columns have the same parameters as a standard normal distribution. Unlike Normalization, standardization maintains useful information about outliers and makes the algorithm less sensitive to them in contrast to min-max scaling, which scales the data to a limited range of values. Here is the formula for standardization.
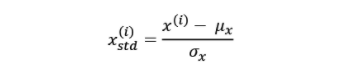
This is how the Python method would look like for standardizing one or more columns:
def standardize(values):
return (values - values.mean())/values.std()
In order to apply the standardization techniques to one or more feature columns, one could use the following Python code (with reference to the dataset used in this post). Note the usage of apply method which applies the standardize method on multiple feature columns all at once.
cols = ['hsc_p', 'ssc_p', 'age', 'height', 'salary']
#
# Standardize the feature columns; Dataframe needs to be recreated for the following command to work properly.
#
df[cols] = df[cols].apply(standardize)
MinMaxScaler for Normalization: Sklearn Python Example
MinMaxScaler is a class from sklearn.preprocessing which is used for normalization. Here is the sample code:
from sklearn.preprocessing import MinMaxScaler
mmscaler = MinMaxScaler()
cols = ['hsc_p', 'ssc_p', 'age', 'height', 'salary']
df[cols] = mmscaler.fit_transform(df[cols])
In case of normalizing the training and test data set, the MinMaxScaler estimator will fit on the training data set and the same estimator will be used to transform both training and the test data set. The following code demonstrates the same assuming X consists of the training data set and y consists of corresponding labels. IRIS data set is used for illustration purposes.
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)
mmscaler = MinMaxScaler()
X_train_norm = mms.fit_transform(X_train)
X_test_norm = mms.transform(X_test)
StandardScaler for Standardization: Sklearn Python Example
StandardScaler is a class from sklearn.preprocessing which is used for standardization. Here is the sample code:
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
cols = ['hsc_p', 'ssc_p', 'age', 'height', 'salary']
df[cols] = sc.fit_transform(df[cols])
In case of standardizing the training and test data set, the StandardScaler estimator will fit on the training data set and the same estimator will be used to transform both training and the test data set. The following code demonstrates the same. IRIS data set is used for illustration purposes.
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)
sc = StandardScaler()
X_train_norm = sc.fit_transform(X_train)
X_test_norm = sc.transform(X_test)
When to use MinMaxScaler or StandardScaler?
MinMaxScaler is useful when the data has a bounded range or when the distribution is not Gaussian. For example, in image processing, pixel values are typically in the range of 0-255. Scaling these values using MinMaxScaler ensures that the values are within a fixed range and contributes equally to the analysis. Similarly, when dealing with non-Gaussian distributions such as a power-law distribution, MinMaxScaler can be used to ensure that the range of values is scaled between 0 and 1.
StandardScaler is useful when the data has a Gaussian distribution or when the algorithm requires standardized features. For example, in linear regression, the features need to be standardized to ensure that they contribute equally to the analysis. Similarly, when working with clustering algorithms such as KMeans, StandardScaler can be used to ensure that the features are standardized and contribute equally to the analysis.
Conclusion
Here are some conclusions you can take away as the learning:
- Feature scaling is about transforming the value of features in the similar range like others for machine learning algorithms to behave better resulting in optimal models.
- Feature scaling is not required for algorithms such as random forest or decision tree
- Standardization and normalization are two most common techniques for feature scaling.
- Normalization is about transforming the feature values to fall within the bounded intervals (min and max)
- Standardization is about transforming the feature values to fall around mean as 0 with standard deviation as 1
- Standardization maintains useful information about outliers and makes the algorithm less sensitive to them in contrast to min-max scaling
- MinMaxScaler class of sklearn.preprocessing is used for normalization of features.
- StandardScaler class of sklearn.preprocessing is used for standardization of features.
- Mathematics Topics for Machine Learning Beginners - July 6, 2025
- Questions to Ask When Thinking Like a Product Leader - July 3, 2025
- Three Approaches to Creating AI Agents: Code Examples - June 27, 2025
I found it very helpful. However the differences are not too understandable for me