What is a Hypothesis testing?
As per the definition from Oxford languages, a hypothesis is a supposition or proposed explanation made on the basis of limited evidence as a starting point for further investigation. As per the Dictionary page on Hypothesis, Hypothesis means a proposition or set of propositions, set forth as an explanation for the occurrence of some specified group of phenomena, either asserted merely as a provisional conjecture to guide investigation (working hypothesis) or accepted as highly probable in the light of established facts.
The hypothesis can be defined as the claim that can either be related to the truth about something that exists in the world, or, truth about something that’s needs to be established a fresh. In simple words, another word for the hypothesis is the “claim”. Until the claim is proven to be true, it is called the hypothesis. Once the claim is proved, it becomes the new truth or new knowledge about the thing. For example, let’s say that a claim is made that students studying for more than 6 hours a day gets more than 90% of marks in their examination. Now, this is just a claim or a hypothesis and not the truth in the real world. However, in order for the claim to become the truth for widespread adoption, it needs to be proved using pieces of evidence, e.g., data. In order to reject this claim or otherwise, one needs to do some empirical analysis by gathering data samples and evaluating the claim. The process of gathering data and evaluating the claims or hypotheses with the goal to reject or otherwise (failing to reject) can be called as hypothesis testing. Note the wordings – “failing to reject”. It means that we don’t have enough evidence to reject the claim. Thus, until the time that new evidence comes up, the claim can be considered the truth. There are different techniques to test the hypothesis in order to reach the conclusion of whether the hypothesis can be used to represent the truth of the world.
One must note that the hypothesis testing never constitutes a proof that the hypothesis is absolute truth based on the observations. It only provides added support to consider the hypothesis as truth until the time that new evidences can against the hypotheses can be gathered. We can never be 100% sure about truth related to those hypotheses based on the hypothesis testing.
Simply speaking, hypothesis testing is a framework that can be used to assert whether the claim or the hypothesis made about a real-world/real-life event can be seen as the truth or otherwise based on the given data (evidences).
Hypothesis Testing Examples
Before we get ahead and start understanding more details about hypothesis and hypothesis testing steps, lets take a look at some real-world examples of how to think about hypothesis and hypothesis testing when dealing with real-world problems:
- Customer churn: Customer churn is one of the most common problem one come across when starting to work with AI / machine learning. Customer churn refers to the process of customers leaving a company or service. It is the percentage of customers who stop doing business with a company in a given time period. Not only does it lose revenue from the customer who leaves, but it also incurs the cost of acquiring a new customer. Thus, business wants to take action to stop the customer churn. In order to take one or more actions, they need to make decisions which will be followed by those actions. These decisions are based on claims or hypothesis made by the business stakeholders in relation to why customer are leaving the services. This is where hypothesis and hypothesis testing comes into picture. Let’s look at some of the hypothesis which can be put to hypothesis testing and later carved into analytical solutions such as dashboards, or AI / machine learning solutions as appropriate.
- Customers are churning because they ain’t getting response to their complaints or issues
- Customers are churning because there are other competitive services in the market which are providing these services at lower cost.
- Customers are churning because there are other competitive services which are providing more services at the same cost.
- It is claimed that a 500 gm sugar packet for a particular brand, say XYZA, contains sugar of less than 500 gm, say around 480gm. Can this claim be taken as truth? How do we know that this claim is true? This is a hypothesis until proved.
- A group of doctors claims that quitting smoking increases lifespan. Can this claim be taken as new truth? The hypothesis is that quitting smoking results in an increase in lifespan.
- It is claimed that brisk walking for half an hour every day reverses diabetes. In order to accept this in your lifestyle, you may need evidence that supports this claim or hypothesis.
- It is claimed that doing Pranayama yoga for 30 minutes a day can help in easing stress by 50%. This can be termed as hypothesis and would require testing / validation for it to be established as a truth and recommended for widespread adoption.
- One common real-life example of hypothesis testing is election polling. In order to predict the outcome of an election, pollsters take a sample of the population and ask them who they plan to vote for. They then use hypothesis testing to assess whether their sample is representative of the population as a whole. If the results of the hypothesis test are significant, it means that the sample is representative and that the poll can be used to predict the outcome of the election. However, if the results are not significant, it means that the sample is not representative and that the poll should not be used to make predictions.
- Machine learning models make predictions based on the input data. Each of the machine learning model representing a function approximation can be taken as a hypothesis. All different models constitute what is called as hypothesis space.
- As part of a linear regression machine learning model, it is claimed that there is a relationship between the response variables and predictor variables? Can this hypothesis or claim be taken as truth? Let’s say, the hypothesis is that the housing price depends upon the average income of people already staying in the locality. How true is this hypothesis or claim? The relationship between response variable and each of the predictor variables can be evaluated using T-test and T-statistics.
- For linear regression model, one of the hypothesis is that there is no relationship between the response variable and any of the predictor variables. Thus, if b1, b2, b3 are three parameters, all of them is equal to 0. b1 = b2 = b3 = 0. This is where one performs F-test and use F-statistics to test this hypothesis.
You may note different hypotheses which are listed above. The next step would be validate some of these hypotheses. This is where data scientists will come into picture. One or more data scientists may be asked to work on different hypotheses. This would result in these data scientists looking for appropriate data related to the hypothesis they are working. This section will be detailed out in near future.
State the Hypothesis to begin Hypothesis Testing
The first step to hypothesis testing is defining or stating a hypothesis. Before the hypothesis can be tested, we need to formulate the hypothesis in terms of mathematical expressions. There are two important aspects to pay attention to, prior to the formulation of the hypothesis. The following represents different types of hypothesis that could be put to hypothesis testing:
- Claim made against the well-established fact: The case in which a fact is well-established, or accepted as truth or “knowledge” and a new claim is made about this well-established fact. For example, when you buy a packet of 500 gm of sugar, you assume that the packet does contain at the minimum 500 gm of sugar and not any less, based on the label of 500 gm on the packet. In this case, the fact is given or assumed to be the truth. A new claim can be made that the 500 gm sugar contains sugar weighing less than 500 gm. This claim needs to be tested before it is accepted as truth. Such cases could be considered for hypothesis testing if this is claimed that the assumption or the default state of being is not true. The claim to be established as new truth can be stated as “alternate hypothesis”. The opposite state can be stated as “null hypothesis”. Here the claim that the 500 gm packet consists of sugar less than 500 grams would be stated as alternate hypothesis. The opposite state which is the sugar packet consists 500 gm is null hypothesis.
- Claim to establish the new truth: The case in which there is some claim made about the reality that exists in the world (fact). For example, the fact that the housing price depends upon the average income of people already staying in the locality can be considered as a claim and not assumed to be true. Another example could be the claim that running 5 miles a day would result in a reduction of 10 kg of weight within a month. There could be varied such claims which when required to be proved as true have to go through hypothesis testing. The claim to be established as new truth can be stated as “alternate hypothesis”. The opposite state can be stated as “null hypothesis”. Running 5 miles a day would result in reduction of 10 kg within a month would be stated as alternate hypothesis.
Based on the above considerations, the following hypothesis can be stated for doing hypothesis testing.
- The packet of 500 gm of sugar contains sugar of weight less than 500 gm. (Claim made against the established fact). This is a new knowledge which requires hypothesis testing to get established and acted upon.
- The housing price depends upon the average income of the people staying in the locality. This is a new knowledge which requires hypothesis testing to get established and acted upon.
- Running 5 miles a day results in a reduction of 10 kg of weight within a month. This is a new knowledge which requires hypothesis testing to get established for widespread adoption.
Formulate Null & Alternate Hypothesis as Next Step
Once the hypothesis is defined or stated, the next step is to formulate the null and alternate hypothesis in order to begin hypothesis testing as described above.
What is a null hypothesis?
In the case where the given statement is a well-established fact or default state of being in the real world, one can call it a null hypothesis (in the simpler word, nothing new). Well-established facts don’t need any hypothesis testing and hence can be called the null hypothesis. In cases, when there are any new claims made which is not well established in the real world, the null hypothesis can be thought of as the default state or opposite state of that claim. For example, in the previous section, the claim or hypothesis is made that the students studying for more than 6 hours a day gets more than 90% of marks in their examination. The null hypothesis, in this case, will be that the claim is not true or real. The null hypothesis can be stated that there is no relationship or association between the students reading more than 6 hours a day and they getting 90% of the marks. Any occurrence is only a chance occurrence. Another example of hypothesis is when somebody is alleged that they have performed a crime.
Null hypothesis is denoted by letter H with 0, e.g., [latex]H_0[/latex]
What is an alternate hypothesis?
When the given statement is a claim (unexpected event in the real world) and not yet proven, one can call/formulate it as an alternate hypothesis and accordingly define a null hypothesis which is the opposite state of the hypothesis. The alternate hypothesis is a new knowledge or truth that needs to be established. In simple words, the hypothesis or claim that needs to be tested against reality in the real world can be termed the alternate hypothesis. In order to reach a conclusion that the claim (alternate hypothesis) can be considered the new knowledge or truth (based on the available evidence), it would be important to reject the null hypothesis. It should be noted that null and alternate hypotheses are mutually exclusive and at the same time asymmetric. In the example given in the previous section, the claim that the students studying for more than 6 hours get more than 90% of marks can be termed as the alternate hypothesis.
Alternate hypothesis is denoted with H subscript a, e.g., [latex]H_a[/latex]
Once the hypothesis is formulated as null([latex]H_0[/latex]) and alternate hypothesis ([latex]H_a[/latex]), there are two possible outcomes that can happen from hypothesis testing. These outcomes are the following:
- Reject the null hypothesis: There is enough evidence based on which one can reject the null hypothesis. Let’s understand this with the help of an example provided earlier in this section. The null hypothesis is that there is no relationship between the students studying more than 6 hours a day and getting more than 90% marks. In a sample of 30 students studying more than 6 hours a day, it was found that they scored 91% marks. Given that the null hypothesis is true, this kind of hypothesis testing result will be highly unlikely. This kind of result can’t happen by chance. That would mean that the claim can be taken as the new truth or new knowledge in the real world. One can go and take further samples of 30 students to perform some more testing to validate the hypothesis. If similar results show up with other tests, it can be said with very high confidence that there is enough evidence to reject the null hypothesis that there is no relationship between the students studying more than 6 hours a day and getting more than 90% marks. In such cases, one can go to accept the claim as new truth that the students studying more than 6 hours a day get more than 90% marks. The hypothesis can be considered the new truth until the time that new tests provide evidence against this claim.
- Fail to reject the null hypothesis: There is not enough evidence-based on which one can reject the null hypothesis (well-established fact or reality). Thus, one would fail to reject the null hypothesis. In a sample of 30 students studying more than 6 hours a day, the students were found to score 75%. Given that the null hypothesis is true, this kind of result is fairly likely or expected. With the given sample, one can’t reject the null hypothesis that there is no relationship between the students studying more than 6 hours a day and getting more than 90% marks.
Examples of formulating the null and alternate hypothesis
The following are some examples of the null and alternate hypothesis.
- Take the example of sugar with the label 500 gm. As per the above, this represents the scenario when the statement made is believed to be true in reality. Thus, it is believe to be true (based on the given label) that the sugar packet weighs 500 gm. The claim, however, is made that the sugar packet with label as 500gm weighs significantly less than 500 gm (around 480 gm). Thus, we will need to do hypothesis testing to find out whether the claim made is true or otherwise. The hypothesis testing would need to be done to ascertain the truth about the label mentioned as 500 gm because there is a claim that sugar packets consisted of 480 gm. In this scenario, the null hypothesis would get formulated as the statement that the weight of canned sugar is equal to 500 gm. The alternate hypothesis will thus get formulated as the statement that the weight of the sugar packet is less than 500 gm.
Null hypothesis The weight of the sugar packet is 500 gm. (A well-established fact) Alternate hypothesis The weight of the sugar packet is less than 500 gm. - Take the example of a claim that running 5 miles a day will lead to a reduction of 10 kg of weight within a month. Now, this is the hypothesis or claim which is required to be proved or otherwise. The alternate hypothesis will be formulated first as the statement that “running 5 miles a day will lead to a reduction of 10 kg of weight within a month”. Hence, the null hypothesis will be the opposite of the alternate hypothesis and stated as the fact that “running 5 miles a day does not lead to a reduction of 10 kg of weight within a month”.
Null hypothesis Running 5 miles a day does not result in the reduction of 10 kg of weight within a month. Alternate hypothesis Running 5 miles a day results in the reduction of 10 kg of weight within a month. - Take another example of a claim that the housing price depends upon the average income of people staying in the locality. This is the claim which is required to be proved or otherwise. The alternate hypothesis will be formulated first as the statement that “housing price depends upon the average income of people staying in the locality”. Hence, the null hypothesis will be formulated as the statement that housing price does NOT depend upon the average income of people staying in the locality.
Null hypothesis The housing price does not depend upon the average income of people staying in the locality. Alternate hypothesis The housing price depends upon the average income of people staying in the locality.
Hypothesis Testing Steps
Here is the diagram which represents the workflow of Hypothesis Testing.
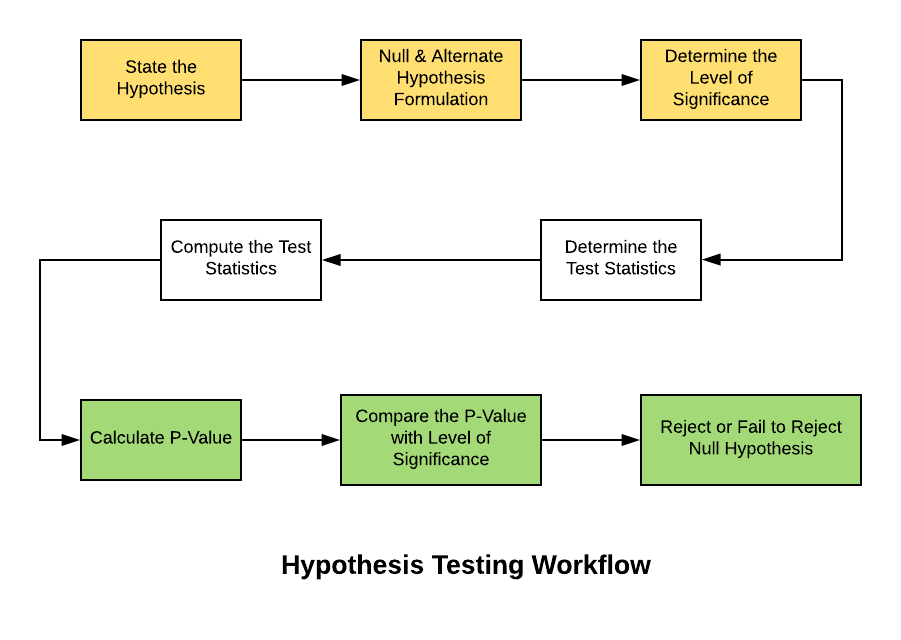
Figure 1. Hypothesis Testing Steps
Based on the above, the following are some of the steps to be taken when doing hypothesis testing:
- State the hypothesis: First and foremost, the hypothesis needs to be stated. The hypothesis could either be the statement that is assumed to be true or the claim which is made to be true.
- Formulate the hypothesis: This step requires one to identify the Null and Alternate hypotheses or in simple words, formulate the hypothesis. Take an example of the canned sauce weighing 500 gm as the Null Hypothesis.
- Set the criteria for a decision: Identify test statistics that could be used to assess the Null Hypothesis. The test statistics with the above example would be the average weight of the sugar packet, and t-statistics would be used to determine the P-value. For different kinds of problems, different kinds of statistics including Z-statistics, T-statistics, F-statistics, etc can be used.
- Identify the level of significance (alpha): Before starting the hypothesis testing, one would be required to set the significance level (also called as alpha) which represents the value for which a P-value less than or equal to alpha is considered statistically significant. Typical values of alpha are 0.1, 0.05, and 0.01. In case the P-value is evaluated as statistically significant, the null hypothesis is rejected. In case, the P-value is more than the alpha value, the null hypothesis is failed to be rejected.
- Compute the test statistics: Next step is to calculate the test statistics (z-test, t-test, f-test, etc) to determine the P-value. If the sample size is more than 30, it is recommended to use z-statistics. Otherwise, t-statistics could be used. In the current example where 20 packets of canned sauce is selected for hypothesis testing, t-statistics will be calculated for the mean value of 505 gm (sample mean). The t-statistics would then be calculated as the difference of 505 gm (sample mean) and the population means (500 gm) divided by the sample standard deviation divided by the square root of sample size (20).
- Calculate the P-value of the test statistics: Once the test statistics have been calculated, find the P-value using either of t-table or a z-table. P-value is the probability of obtaining a test statistic (t-score or z-score) equal to or more extreme than the result obtained from the sample data, given that the null hypothesis H0 is true.
- Compare P-value with the level of significance: The significance level is set as the allowable range within which if the value appears, one will be failed to reject the Null Hypothesis. This region is also called as Non-rejection region. The value of alpha is compared with the p-value. If the p-value is less than the significance level, the test is statistically significant and hence, the null hypothesis will be rejected.
P-Value: Key to Statistical Hypothesis Testing
Once you formulate the hypotheses, there is the need to test those hypotheses. Meaning, say that the null hypothesis is stated as the statement that housing price does not depend upon the average income of people staying in the locality, it would be required to be tested by taking samples of housing prices and, based on the test results, this Null hypothesis could either be rejected or failed to be rejected. In hypothesis testing, the following two are the outcomes:
- Reject the Null hypothesis
- Fail to Reject the Null hypothesis
Take the above example of the sugar packet weighing 500 gm. The Null hypothesis is set as the statement that the sugar packet weighs 500 gm. After taking a sample of 20 sugar packets and testing/taking its weight, it was found that the average weight of the sugar packets came to 495 gm. The test statistics (t-statistics) were calculated for this sample and the P-value was determined. Let’s say the P-value was found to be 15%. Assuming that the level of significance is selected to be 5%, the test statistic is not statistically significant (P-value > 5%) and thus, the null hypothesis fails to get rejected. Thus, one could safely conclude that the sugar packet does weigh 500 gm. However, if the average weight of canned sauce would have found to be 465 gm, this is way beyond/away from the mean value of 500 gm and one could have ended up rejecting the Null Hypothesis based on the P-value.
Hypothesis Testing for Problem Analysis & Solution Implementation
Hypothesis testing can be applied in both problem analysis and solution implementation. The following represents method on how you can apply hypothesis testing technique for both problem and solution space:
- Problem Analysis: Hypothesis testing is a systematic way to validate assumptions or educated guesses during problem analysis. It allows for a structured investigation into the nature of a problem and its potential root causes. In this process, a null hypothesis and an alternative hypothesis are usually defined. The null hypothesis generally asserts that no significant change or effect exists, while the alternative hypothesis posits the opposite. Through controlled experiments, data collection, or statistical analysis, these hypotheses are then tested to determine their validity. For example, if a software company notices a sudden increase in user churn rate, they might hypothesize that the recent update to their application is the root cause. The null hypothesis could be that the update has no effect on churn rate, while the alternative hypothesis would assert that the update significantly impacts the churn rate. By analyzing user behavior and feedback before and after the update, and perhaps running A/B tests where one user group has the update and another doesn’t, the company can test these hypotheses. If the alternative hypothesis is confirmed, the company can then focus on identifying specific issues in the update that may be causing the increased churn, thereby moving closer to a solution.
- Solution Implementation: Hypothesis testing can also be a valuable tool during the solution implementation phase, serving as a method to evaluate the effectiveness of proposed remedies. By setting up a specific hypothesis about the expected outcome of a solution, organizations can create targeted metrics and KPIs to measure success. For example, if a retail business is facing low customer retention rates, they might implement a loyalty program as a solution. The hypothesis could be that introducing a loyalty program will increase customer retention by at least 15% within six months. The null hypothesis would state that the loyalty program has no significant effect on retention rates. To test this, the company can compare retention metrics from before and after the program’s implementation, possibly even setting up control groups for more robust analysis. By applying statistical tests to this data, the company can determine whether their hypothesis is confirmed or refuted, thereby gauging the effectiveness of their solution and making data-driven decisions for future actions.
References
Hypothesis testing quiz
[wp_quiz id=”11360″]
Summary
In this post, you learned about hypothesis testing and related nuances such as the null and alternate hypothesis formulation techniques, ways to go about doing hypothesis testing etc. In data science, one of the reasons why one needs to understand the concepts of hypothesis testing is the need to verify the relationship between the dependent (response) and independent (predictor) variables. One would, thus, need to understand the related concepts such as hypothesis formulation into null and alternate hypothesis, level of significance, test statistics calculation, P-value, etc. Given that the relationship between dependent and independent variables is a sort of hypothesis or claim, the null hypothesis could be set as the scenario where there is no relationship between dependent and independent variables.
- Mathematics Topics for Machine Learning Beginners - July 6, 2025
- Questions to Ask When Thinking Like a Product Leader - July 3, 2025
- Three Approaches to Creating AI Agents: Code Examples - June 27, 2025
I found it very helpful. However the differences are not too understandable for me