In the ever-evolving world of data science, extracting meaningful insights from diverse data sets is a fundamental task. However, a significant problem arises when these data sets do not conform to the assumptions of normality and equal variances, rendering popular parametric tests like the t-test ineffectual. Real-world data often tends to be skewed, includes outliers, or originates from an unknown distribution. For instance, data related to salaries, house prices, or user behavior metrics often challenge traditional statistical methods.
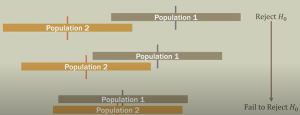
This is where the Wilcoxon Rank Sum Test, also known as the Mann-Whitney U test, proves to be an invaluable statistical test. As a non-parametric alternative to the independent two-sample t-test, it is designed to handle data that doesn’t meet the assumptions of parametric tests. It is similar to the Student’s t-test, but does not require the assumption of normality. The test is appropriate for use with small sample sizes.
What is Wilcoxon Rank Sum / Mann-Whitney U Test?
The Wilcoxon Rank Sum Test, also known as the Mann-Whitney U test, is a non-parametric statistical hypothesis test that is used to compare two independent samples to assess whether their populations have the same distribution. Nonparametric tests, such as the Wilcoxon Rank Sum Test, make fewer assumptions about the data’s distribution and are particularly useful when dealing with skewed data or data with outliers. The Wilcoxon rank sum test is also known as Mann-Whitney test, Mann-Whitney-Wilcoxon test, Wilcoxon Two-Sample Test, or Wilcoxon rank sum statistics test.
Similar to the independent two-samples t-test, the Wilcoxon Rank Sum Test aims to determine if there is a significant difference between two groups. However, while the t-test assumes that the data is normally distributed and the variances are equal across the two groups, the Wilcoxon Rank Sum Test does not make these assumptions. Instead, it operates on the ranks of the data rather than their raw values, making it more robust to outliers and non-normality.
The Wilcoxon Rank Sum Test works in several steps that involve ranking the data from both samples and then comparing these ranks. We will understand each of the following steps with this data example. Let’s assume we have two sets of observations. These could represent anything – for example, the time spent on a website for two different user groups A and B:
Group A: [5, 8, 6, 7, 9]
Group B: [6, 7, 4, 5, 8]
The following represents how this statistical test works with reference to the above data.
-
Combine and Rank the Data: The first step in the Wilcoxon Rank Sum Test is to combine all the data from the two samples into a single set. Then, each observation in this combined set is ranked, from the smallest to the largest. If two or more observations have the same value (i.e., there are ties), they receive a rank equal to the average of the ranks they would have received had they been slightly different. The above reference data after being combined and ranked looks like the following:
Combined data: [4, 5, 5, 6, 6, 7, 7, 8, 8, 9]
Ranks: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] -
Calculate Rank Sums: Next, the ranks for the observations from each of the original samples are added up separately. This gives us two rank sums.
Group A ranks: [2.5, 9, 4.5, 7, 10] Sum = 33
Group B ranks: [4.5, 7, 1, 2.5, 9] Sum = 24
Note: When we have ties, we assign them the average rank. For example, we have 5 and 6 twice, so we assigned them average ranks (2+3)/2=2.5 for 5, and (4+5)/2=4.5 for 6. -
Calculate Test Statistic: The test statistic (W) for the Wilcoxon Rank Sum Test is the smaller of the two rank sums.
In the example, the test statistic W is the smaller of the two rank sums, which is 24. -
Determine Significance: The null hypothesis of the Wilcoxon Rank Sum Test is that the distributions of the two populations are identical. Therefore, if there is a significant difference between the rank sums of the two groups, we reject the null hypothesis. The exact distribution of W under the null hypothesis is known, so we can compare our test statistic to this distribution to determine the p-value. If the p-value is less than our chosen significance level (often 0.05), we reject the null hypothesis.
We could use statistical tables or a statistical software package (like Python’s SciPy) to determine the p-value associated with our test statistic given our sample sizes. -
Interpret the Result: If the result is significant, we conclude that there’s a difference between the distributions of the two populations. The direction of the difference (which population tends to have larger values) can be determined by looking at which sample had the larger rank sum.
Wilcoxon Rank Sum / Mann-Whitney U Test – Python Example
Here is the Python code using the SciPy library to perform the Wilcoxon Rank Sum Test. In the code below, scipy.stats.ranksums function performs the Wilcoxon Rank Sum Test. The ranksums function returns two values: the test statistic and the p-value.
from scipy.stats import ranksums
# Define your two samples
group_A = [5, 8, 6, 7, 9]
group_B = [6, 7, 4, 5, 8]
# Perform the Wilcoxon Rank Sum Test
statistic, pvalue = ranksums(group_A, group_B)
# Print the results
print('Test statistic:', statistic)
print('p-value:', pvalue)
The following will get printed:
Test statistic: 0.9400193421607683
p-value: 0.34720763934942456
The test statistic value is approximately 0.94. This value is a measure of the difference between the two samples. The sign of the test statistic indicates the direction of the difference. A positive value suggests that values in the first sample are typically larger than those in the second, while a negative value suggests the opposite. However, the test statistic alone doesn’t provide us with enough information to make a definitive conclusion about the significance of this difference.
The p-value is approximately 0.347. This value represents the probability of observing a test statistic as extreme as the one calculated (0.94 in this case) under the null hypothesis (the assumption that there is no difference between the populations from which the two samples were drawn).
Typically, a threshold (often 0.05) is chosen to determine whether the p-value is low enough to reject the null hypothesis. This threshold is known as the significance level (α). If the p-value is less than α, we reject the null hypothesis and conclude that there is a significant difference between the two groups.
In this case, the p-value is larger than 0.05. This suggests that the evidence is not strong enough to reject the null hypothesis. Therefore, we would conclude that there is no statistically significant difference between the two groups based on the Wilcoxon Rank Sum Test with the data given.
Real-world Applications: The Wilcoxon Rank Sum Test
The Wilcoxon Rank Sum Test, also known as the Mann-Whitney U test, is used to test whether the two samples originate from the same distribution, and is particularly effective when the assumptions of normality, which is required for a standard t-test, are violated. Let’s dive into three real-world scenarios where this test is applied.
Evaluating Teaching Methods
Suppose a school is trying to evaluate the effectiveness of two different teaching methods. The school conducts a study where one group of students is taught with method A and another group with method B. The null and alternative hypotheses would be as follows:
Null hypothesis (H0): There is no difference in the median exam scores between students taught with method A and those taught with method B.
Alternative hypothesis (H1): The median exam score of students taught with method A is different from those taught with method B.
The Wilcoxon Rank Sum Test would be used to compare the distributions of exam scores for the two groups, providing an objective basis for comparing the teaching methods.
Comparing Drug Efficacy
Consider a pharmaceutical company that has developed a new drug to lower blood pressure and wants to compare its effectiveness to an existing treatment. Patients are randomly assigned to either the new drug or the existing treatment, and their blood pressure reductions are measured.
Null hypothesis (H0): There is no difference in the median blood pressure reduction between patients treated with the new drug and those treated with the existing one.
Alternative hypothesis (H1): The median blood pressure reduction is different between patients treated with the new drug and those treated with the existing one.
Here, the Wilcoxon Rank Sum Test would be an appropriate statistical test to compare the two treatments if the blood pressure reductions are not normally distributed.
Assessing Customer Satisfaction
Suppose a retail company has two stores in different locations and wants to compare customer satisfaction levels between the two. The company collects satisfaction ratings (on a scale of 1 to 10) from customers at both stores.
Null hypothesis (H0): There is no difference in the median customer satisfaction levels between Store A and Store B.
Alternative hypothesis (H1): The median customer satisfaction levels are different between Store A and Store B.
The Wilcoxon Rank Sum Test could be used to determine if the distributions of customer satisfaction levels at the two stores are significantly different, particularly if the satisfaction scores are not normally distributed.
Conclusion
The Wilcoxon rank sum test is a non-parametric statistical hypothesis test used to compare two samples. It does not require the assumption of normality, and so it is appropriate for use with small sample sizes. The test works by calculating the sum of ranks for each sample, and if the p-value is less than 0.05, then the null hypothesis is rejected in favor of the alternative hypothesis. When interpreting results of Wilcoxon rank sum test, it is important to remember that the null hypothesis states that there is no difference between the two samples while the alternative hypothesis states that there is a difference between the two samples.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me