In this post, you will learn about SVM (Support Vector Machine) as Soft Margin Classifier and the importance of Value of C. In the previous post, we learned about SVM as maximum margin classifier.
What & Why of SVM as Soft Margin Classifier?
Before getting into understanding what is Soft Margin Classifier version of SVM algorithm, lets understand why we need it when we had a maximum margin classifier.
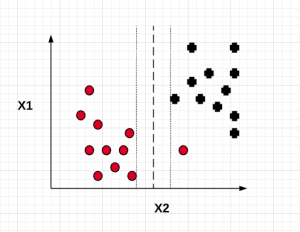
Maximum margin classifier works well with linearly separable data such as the following:
When maximum margin classifier is trained on the above data set with maximum distance (margin) between the closest points (support vectors), we can get a hyperplane which can separate the data in a clear manner and one can predict the class of the future data in with a very high accuracy. This is how the maximum margin classifier would look like:
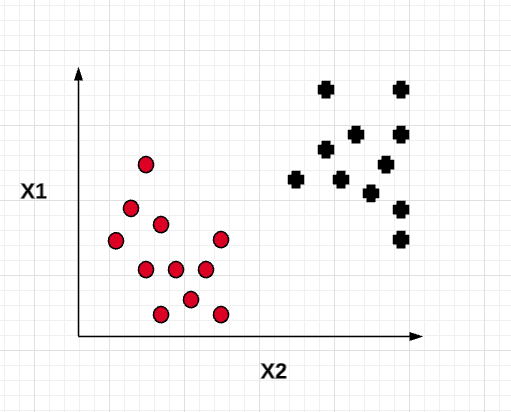
However, in the real world, the data is not linearly separable and trying to fit in a maximum margin classifier could result in overfitting the model (high variance). Here is an instance of non-linearly separable data:
For the above data set which is non-linear and not easily separable, trying to fit a maximum margin classifier can result in a model such as the following which looks to be an overfitted model with a high variance. It gets difficult for training to converge. The model may fail to generalize for the larger population.
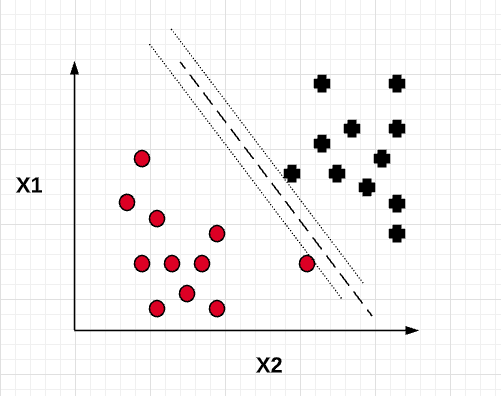
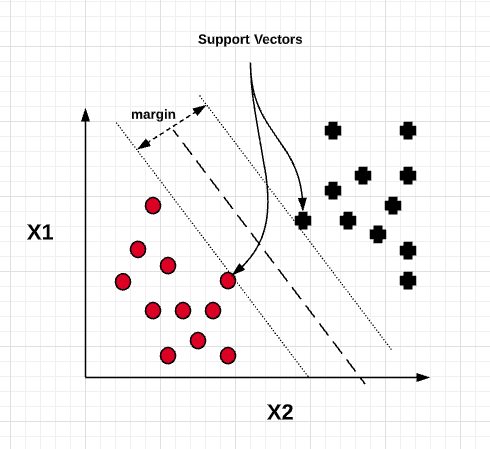
Based on the above, the goal is to come up with a model which can generalize better. This is where the soft margin classifier comes into picture. The idea is to allow the linear constraints used for maximum margin classifier to get a little relaxed for non-linearly separable data in order to allow the convergence of the optimization in the presence of misclassifications, under appropriate cost penalization. Such a soft margin classifier can be represented using the following diagram. Note that one of the points get misclassified. However, the model turns out to be having lower variance than the maximum margin classifier and thus, generalize better. This is achieved by introducing a slack variable , epsilon to the linear constraint functions.
On one side, the constraint function representing the line/hyperplane touching the black + sign looks like the following with the slack variable.
[latex]
W_0 + W^TX_{pos} \geq 1 – \epsilon
[/latex]
On another side, the constraint function representing the line/hyperplane touching the red circle sign looks like the following with the slack variable.
[latex]
W_0 + W^TX_{neg} \leq -1 + \epsilon
[/latex]
The objective function which is minimized becomes the following as a result of introducing a slack variable and another variable called C.
[latex]
\frac{(\lVert w \rVert)^2}{2} + C(\sum_{i} \epsilon)
[/latex]
Importance of C Value
The C value in the above objective function controls the penalty of misclassification. Large value of C would result in higher penalty for misclassification and smaller value of C will result in smaller penalty of misclassification.
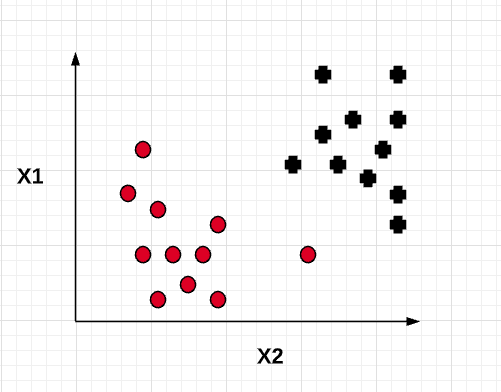
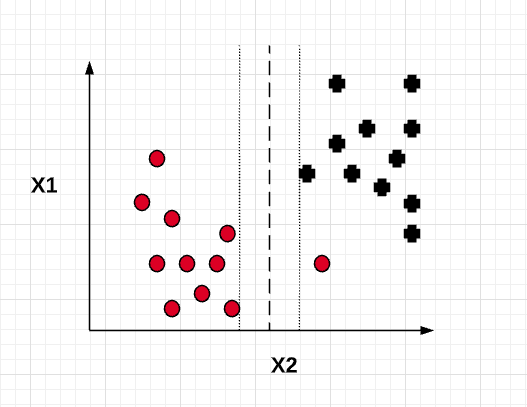
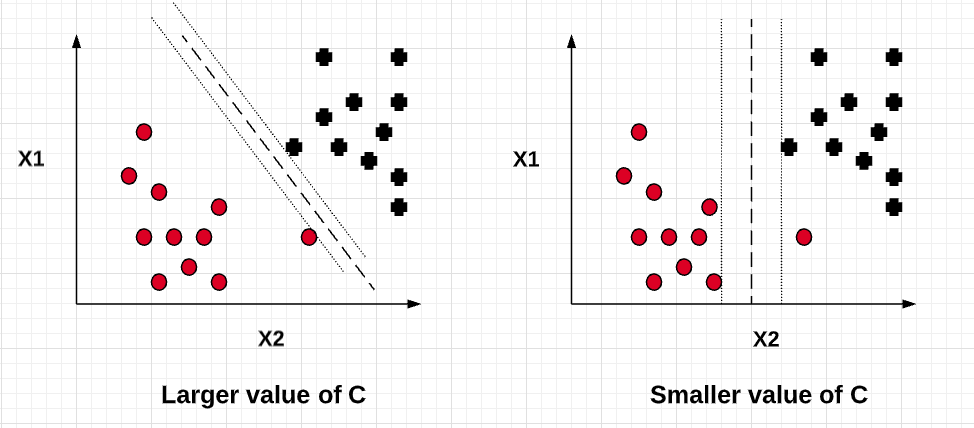
Thus, with a larger value of C, the value of slack variable will be very minimal resulting in model similar to maximum margin classifier. This will turn out to be an overfitted model with high variance. Similarly, smaller value of C will result in a little higher value of slack variable resulting in a model (soft margin classifier) which allows for few data points to be misclassified but results in a model having lesser variance and higher bias than the maximum margin classifier. In other words, the value of C can be used to control the width of the margin. Larger the value of C, the margin width tends to become lesser as shown in the diagram below.
Increasing the value of C decreases the bias and increases the variance while decreasing the value of C increases the bias while lowering the variance. The goal is to find optimum value of C for bias-variance trade-off.
The diagram given below represents the models with different value of C.
In the following post, we will look at the code example in relation to training soft margin classifier using different value of C.
- Mathematics Topics for Machine Learning Beginners - July 6, 2025
- Questions to Ask When Thinking Like a Product Leader - July 3, 2025
- Three Approaches to Creating AI Agents: Code Examples - June 27, 2025
I found it very helpful. However the differences are not too understandable for me