Last updated: 8th Sep, 2024
Confusion among data scientists regarding whether to use ROC Curve / AUC, or, Accuracy / precision / recall metrics for evaluating classification models often stems from misunderstanding ROC Curve / AUC concepts. The ROC Curve visualizes true positive vs false positive rates at various thresholds, while AUC quantifies the overall ability of a model to discriminate between classes, with higher values indicating better performance. In this post, you will learn about ROC Curve and AUC concepts along with related concepts such as True positive and false positive rate with the help of Python examples. It is very important to learn ROC, AUC and related concepts as it helps in selecting the most appropriate machine learning classification models based on the model performance.
What is ROC Curve & AUC / AUROC?
Receiver operating characteristic (ROC) Curve plots the true-positive rate (TPR) against the false-positive rate (FPR) at various probability thresholds. TPR & FPR metrics are computed by shifting the decision threshold of the classifier. TPR is also known as Recall or Sensitivity, and FPR can be understood as the ratio of negative instances that are incorrectly classified as positive ones. FPR can also be represented as (1 – Specificity).
ROC curve is used for selecting the most appropriate classification models that are also probabilistics models that predic the probabilities of the class. Note that while accuracy score, precision, recall, and F1 score apply to binary classification and multiclass classification models, ROC curve metric only applies to binary classification models.
Here is a great paper to read and learn about ROC curve and AUC – A Relationship between the Average Precision and the Area Under the ROC Curve by Su, W., Yuan, Y., and Zhu, M
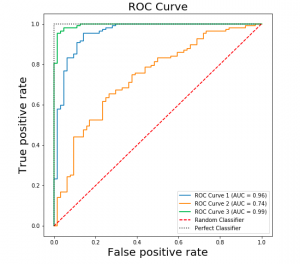
Let’s look at a sample ROC curve given below:
In the above ROC curve diagram, pay attention to some of the following:
- Different ROC curves – Different models: There are different curves (red, green, orange, blue, etc) pertaining to different models. These models can be different owing to the fact that they could be trained using different hyper parameters.
- Diagonal line – Random Guessing: The dashed red line stretching from the lower left to the upper right would indicate that the model gets it right just 50% of the time, which is no better than guessing for a binary classifier.
- Better models: The model with ROC curve above red dashed line can be considered as better than random guessing and could be considered for adoption. The more the curve arches toward the upper-left corner, the more accurate the model.
- Worse models: The model with ROC curve below red dashed line can be considered as worse than random guessing and should be rejected.
- Points on ROC Curve: The points on each ROC curve represent the decision thresholds and related values of true positive rate and false positive rate. Different thresholds result in different values of TPR and FPR and accordingly different overall model performance.
- Ideal decision threshold: Idea decision threshold can be one which results in very high value of TPR (close to 1) and very low value of FPR (close to 0)
- AUROC: AUROC represents Area Under ROC Curve (AUROC). The area under ROC curve is computed to characterise the performance of a classification model. The area under the curve (AUC, or ROC AUC) is used as an overall measure of accuracy. Higher the AUC or AUROC, better the model is at predicting 0s as 0s and 1s as 1s.
Scikit provides a class named RocCurveDisplay for plotting ROC curves, and a function named roc_auc_score for retrieving ROC AUC scores. Scores returned by this function are values from 0.0 to 1.0. The higher the score, the more accurate the model.
Here is an example of different ROC Curves and AUCs. The ROC-AUC between 0.9 to 1.0 (Top and bottom left) is considered very good.
Let’s understand why ideal decision thresholds is about TPR close to 1 and FPR close to 0.
True Positive Rate (TPR) = True Positive (TP) / (TP + FN) = TP / Positives
False Positive Rate (FPR) = False Positive (FP) / (FP + TN) = FP / Negatives
Higher value of TPR would mean that the value of false negative is very low which would mean almost all positives are predicted correctly.
Lower value of FPR would mean that the value of false positive is very low which means almost all negatives are predicted correctly.
Going by the above, the decision threshold near top left of ROC curve would result in the model having optimal performance. In the above diagram, the point is represented using “Perfect Classifier”
ROC Curve and AUC have been found to be used as classification models evaluation metrics in several Kaggle competitions. Here is a list of some of them:
ROC & AUC Explained with Python Examples
In this section, you will learn to use roc_curve and auc method of sklearn.metrics. Sklearn breast cancer dataset is used for illustrating ROC curve and AUC. Pay attention to some of the following in the code given below.
- Method roc_curve is used to obtain the true positive rate and false positive rate at different decision thresholds. Method roc_curve is passed the test labels, the probability of the class and the position of the positive class (pos_label).
- Method auc is used to obtain the area under the ROC curve. Method AUC is passed false positive rate and true positive rate.
- Three different ROC curves is drawn using different features.
- Method predict_proba is used to get the value of probabilities of all the classes.
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
from sklearn.pipeline import make_pipeline
#
# Load the breast cancer data set
#
bc = datasets.load_breast_cancer()
X, y = bc.data, bc.target
#
# Create training and test split
#
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=1, stratify=y)
#
# Create the estimator - pipeline
#
pipeline = make_pipeline(StandardScaler(), LogisticRegression(random_state=1))
#
# Create training test splits using two features
#
pipeline.fit(X_train[:,[2, 13]],y_train)
probs = pipeline.predict_proba(X_test[:,[2, 13]])
fpr1, tpr1, thresholds = roc_curve(y_test, probs[:, 1], pos_label=1)
roc_auc1 = auc(fpr1, tpr1)
#
# Create training test splits using two different features
#
pipeline.fit(X_train[:,[4, 14]],y_train)
probs2 = pipeline.predict_proba(X_test[:,[4, 14]])
fpr2, tpr2, thresholds = roc_curve(y_test, probs2[:, 1], pos_label=1)
roc_auc2 = auc(fpr2, tpr2)
#
# Create training test splits using all features
#
pipeline.fit(X_train,y_train)
probs3 = pipeline.predict_proba(X_test)
fpr3, tpr3, thresholds = roc_curve(y_test, probs3[:, 1], pos_label=1)
roc_auc3 = auc(fpr3, tpr3)
fig, ax = plt.subplots(figsize=(7.5, 7.5))
plt.plot(fpr1, tpr1, label='ROC Curve 1 (AUC = %0.2f)' % (roc_auc1))
plt.plot(fpr2, tpr2, label='ROC Curve 2 (AUC = %0.2f)' % (roc_auc2))
plt.plot(fpr3, tpr3, label='ROC Curve 3 (AUC = %0.2f)' % (roc_auc3))
plt.plot([0, 1], [0, 1], linestyle='--', color='red', label='Random Classifier')
plt.plot([0, 0, 1], [0, 1, 1], linestyle=':', color='green', label='Perfect Classifier')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.legend(loc="lower right")
plt.show()
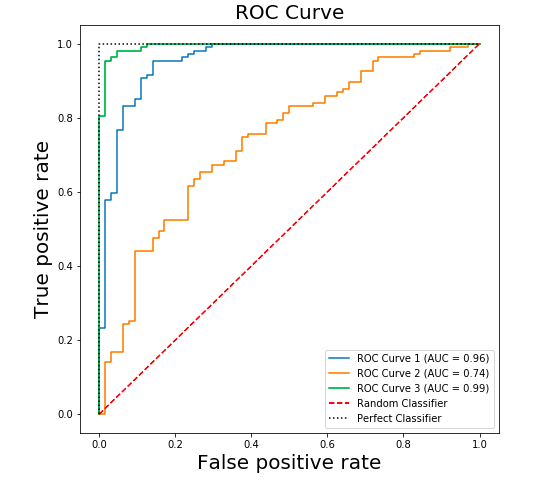
Here is how the ROC curve plot will look like. Pay attention to some of the following in the plot:
- Red dashed line represents the random guessing
- Black dashed line towards top left represents the best / perfect classifier
- Other classifier have different AUC value and related ROC curve.
Conclusions
Here is what you learned in this post in relation to ROC curve and AUC:
- ROC curve is used for probabilistic models which predicts the probability of one or more classes.
- ROC curve is used to select the most appropriate models based on the model performance
- ROC curve is a plot of true positive and false positive rate values which get determined based on different decision thresholds for a particular model.
- Different ROC curves can be created based on different features, model hyper parameters etc.
- AUC or AUROC is area under ROC curve. The value of AUC characterizes the model performance. Higher the AUC value, higher the performance of the model.
- The perfect classifier will have high value of true positive rate and low value of false positive rate.
- Any model with ROC curve above random guessing classifier line can be considered as a better model.
- Any model with ROC curve below random guessing classifier line can outrightly be rejected.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me