Accuracy, Precision, Recall & F1-Score – Python Examples

Last updated: 29th Dec, 2023

Classification models are used in classification problems to predict the target class of the data sample. The classification machine learning models predicts the probability that each instance belongs to one class or another. It is important to evaluate the performance of the classifications model in order to reliably use these models in production for solving real-world problems. The performance metrics include accuracy, precision, recall, and F1-score. Because it helps us understand the strengths and limitations of these models when making predictions in new situations, model performance is essential for machine learning. The most common question asked is what is accuracy, precision, recall and f1 score?

In this blog post, we will explore these classification model performance metrics such as precision score, recall score, accuracy score and F1-score through Python Sklearn example. As a data scientist, you must get a good understanding of concepts related to the above in relation to measuring classification models performance.

Before we get into the details of the metrics as listed above, lets understand key terminologies such as true positive, false positive, true negative and false negative with the help of confusion matrix.

Terminologies – True Positive, False Positive, True Negative, False Negative

Before we get into the definitions, lets work with Sklearn breast cancer datasets for classifying whether a particular instance of data belongs to benign or malignant breast cancer class. The target labels in the breast cancer dataset are Benign (1) and Malignant (0). There are 212 records with labels as malignant and 357 records with labels as benign. Splitting the dataset into training and test set results in the test set consisting 63 records’ labels as malignant and 108 records’ labels as benign. Thus, the actual negative is 108 records and the actual positive is 63 records.  The confusion matrix represented below can help in understanding the concepts of true/false positives and true/false negatives.

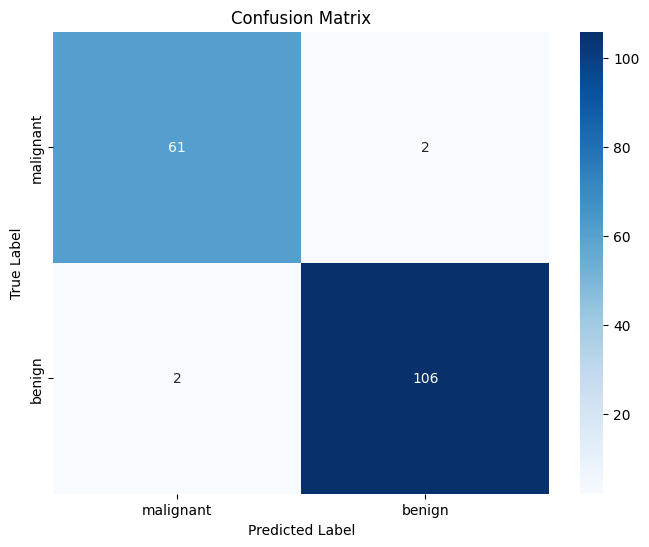
From the confusion matrix, we see that:

• The model predicted 61 cases as malignant, which were actually malignant (True Positives). True positive measures the extent to which the model correctly predicts the positive class. True positives are relevant when we want to know how many positives our model correctly predicts.
• The model correctly identified 106 cases as malignant (True Negatives). A false negative occurs when a model predicts an instance as negative when it is actually positive. False negatives can be very costly, especially in the field of medicine. For example, if a cancer screening test predicts that a patient does not have cancer when they actually do, this could lead to the disease progressing without treatment.
• The model incorrectly predicted 2 cases as malignant that were actually benign (False Positives). False positives occur when the model predicts that an instance belongs to the positive class that it actually does not. The false positive rate is the proportion of all negative examples that are predicted as positive. While false positives may seem like they would be bad for the model, in some cases they can be desirable. For example, in medical applications, it is often better to err on the side of caution and have a few false positives than to miss a diagnosis entirely.
• It incorrectly predicted 2 cases as benign that were actually malignant (False Negatives). False negatives can often become more serious than false positives, and so it is important to take them into account when evaluating the performance of a classification model.

Given the above definitions, let’s try and understand the concept of accuracy, precision, recall, and f1-score.

What is Precision Score?

Precision score in machine learning measures the proportion of positively predicted labels that are actually correct. Precision is also known as the positive predictive value. Precision score is used in conjunction with the recall score to trade-off false positives and false negatives. Precision score is affected by the class distribution. If there are more samples in the minority class, then precision will be lower. If we want to minimize false positives, we would choose a model with high precision. Conversely, if we want to minimize false negatives, we would choose a model with high recall. Precision is mainly used when we need to predict the positive class and there is a greater cost associated with false positives than with false negatives such as in medical diagnosis or spam filtering. For example, if a model is 99% accurate but only has 50% precision, that means that half of the time when it predicts an email is a spam, it is actually not spam. The following is the formula for how to calculate precision score:

Precision Score = True Positives/ (False Positives + True Positives)

From the above formula, you could notice that the value of false-positive would impact the precision score. Thus, when building predictive models with high precision, you may choose to build models with lower false positives.

The precision score from the above confusion matrix will come out to be the following:

Precision score = 61 / (2 + 61) = 61/63 = 0.968

How to calculate Precision in Python?

The same score can be obtained by using the precision_score method from sklearn.metrics given y_test represents the actual labels of the test dataset and y_pred represents its prediction.

print('Precision: %.3f' % precision_score(y_test, y_pred))

Real-world scenarios when precision scores can be used as evaluation metrics

Example #1: Oncologists ideally want models that can identify all cancerous lesions without any or very minimal false-positive results, and hence one could use a precision score in such cases. Note that a greater number of false positives will result in a lot of stress for the patients in general although that may not turn out to be fatal from a health perspective. Further tests will be able to negate the false positive prediction.

Example #2: In credit card fraud detection problems, classification models are evaluated using the precision score to determine how many positive samples were correctly classified by the classification model. You would not like to have a high number of false positives or else you might end up blocking many credit cards and hence a lot of frustrations with the end-users.

Example #3: A greater number of false positives in a spam filter would mean that one or more important emails could be tagged as spam and moved to spam folders. This could hamper in so many different ways including impact on your day-to-day work.

What is Recall Score?

Recall score in machine learning represents the model’s ability to correctly predict the positives out of actual positives. This is unlike precision which measures how many predictions made by models are actually positive out of all positive predictions made. For example: if your model is trying to identify positive reviews, the recall score would be what percent of those positive reviews did it correctly predict as a positive. Recall is also known as sensitivity or the true positive rate.

The higher the recall score, the better the model is at identifying both positive and negative examples. Conversely, a low recall score indicates that the model is not good at identifying positive examples.

Recall score is often used in conjunction with other performance metrics, such as precision score and accuracy, to get a complete picture of the model’s performance. The following is the formula for how to calculate recall score.

Recall Score = True Positives / (False Negatives + True Positives)

From the above formula, you could notice that the value of false-negative would impact the recall score. Thus, it is desirable to build models with lower false negatives if a high recall score is important for the business requirements.

The recall score from the above confusion matrix will come out to be the following:

Recall score = 61 / (2 + 61) = 61/63 = 0.968

How to calculate Recall in Python?

The recall score can be obtained by using the recall_score method from sklearn.metrics

print('Recall: %.3f' % recall_score(y_test, y_pred))

Recall score can be used in the scenario where the labels are not equally divided among classes. For example, if there is a class imbalance ratio of 20:80 (imbalanced data), then the recall score will be more useful than accuracy because it can provide information about how well the machine learning model identified rarer events.

Real-world scenarios when recall scores can be used as evaluation metrics

Recall score in machine learning is an important metric to consider when measuring the effectiveness of your models. It can be used in a variety of real-world scenarios, and it’s important to always aim to improve recall and precision scores together. The following are examples of some real-world scenarios where recall scores can be used as evaluation metrics:

• Example #1: In medical diagnosis, the recall score should be an extremely high otherwise greater number of false negatives would prove to be fatal to the life of patients. The lower recall score would mean a greater false negative which essentially would mean that some patients who are positive are termed as falsely negative. That would mean that patients would get assured that he/she is not suffering from the disease and therefore he/she won’t take any further action. That could result in the disease getting aggravated and prove fatal to life.
• Example #2: In manufacturing, it is important to identify defects in products as early as possible to avoid producing faulty products and wasting resources. The classification models can be trained to identify defects and anomalies. A high recall score is important in this scenario because it indicates that the model is able to correctly identify all instances of defects, including those that may be rare or difficult to detect. A model with a low recall score may miss some instances of defects, leading to faulty products and potential safety issues for consumers.
• Example #3: In a credit card fraud detection system, you would want to have a higher recall score for predicting fraud transactions. A lower recall score would mean a higher false-negative which would mean greater fraud and hence loss to business in terms of upset users.

Precision – Recall Score Tradeoff

The precision-recall score tradeoff is a common issue that arises when evaluating the performance of a classification model. These metrics are often in conflict with each other.

In general, increasing the precision score of a model will decrease its recall score, and vice versa. This is because precision and recall are inversely related – improving one will typically result in a decrease in the other. For example, a model with a high precision score will make few false positive predictions, but it may also miss some true positive cases. On the other hand, a model with a high recall will correctly identify most of the true positive cases, but it may also make more false positive predictions.

In order to evaluate the model, it is important to consider both recall and precision score, rather than just one of these metrics. The appropriate balance between precision-recall score will depend on the specific goals and requirements of the model, as well as the characteristics of the dataset. In some cases, it may be more important to have a high precision (e.g. in medical diagnosis), while in others, a high recall may be more important (e.g. in fraud detection).

To balance precision recall score in machine learning, practitioners often use the F1 score, which is a combination of the two metrics. It is discussed in the later section. However, even the F1 score is not a perfect solution, as it can be difficult to determine the optimal balance between precision recall score for a given application.

Here is detailed write up on scikit-learn website on precision-recall metric.

What is Accuracy Score?

Accuracy score is the metrics that is defined as the ratio of true positives and true negatives to all positive and negative observations. In other words, accuracy tells us how often we can expect our machine learning model will correctly predict an outcome out of the total number of times it made predictions. For example: Let’s assume that you were testing your model with a dataset of 100 records and that your machine learning model predicted all 90 of those instances correctly. The accuracy metric, in this case, would be: (90/100) = 90%. The accuracy rate is great but it doesn’t tell us anything about the errors our machine learning models make on new data we haven’t seen before. The following is the formula of the accuracy score.

Accuracy Score = (TP + TN)/ (TP + FN + TN + FP)

The accuracy score from above confusion matrix will come out to be the following:

Accuracy score = (61 + 106) / (61 + 2 + 106 + 2) = 167/171 = 0.977

How to calculate Accuracy score in Python?

The same score can be obtained by using accuracy_score method from sklearn.metrics

print('Accuracy: %.3f' % accuracy_score(y_test, y_pred))

Caution with Accuracy Score

The following are some of the issues with accuracy metrics / score:

• The same accuracy metrics for two different models may indicate different model performance towards different classes.
• In case of imbalanced dataset, accuracy metrics is not the most effective metrics to be used.

One should be cautious when relying on the accuracy metrics of model to evaluate the model performance. Take a look at the following confusion matrix. For model accuracy represented using both the cases (left and right), the accuracy is 60%. However, both the models exhibit different behaviors.

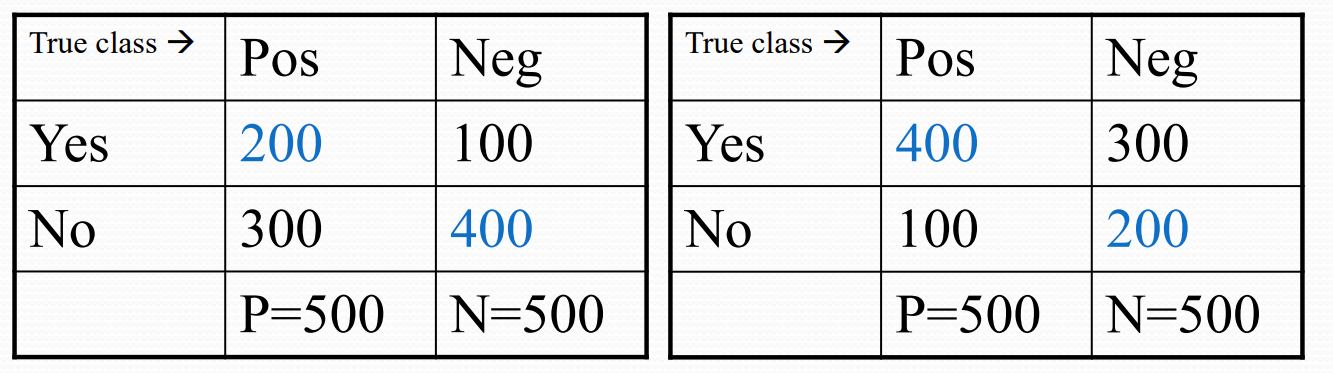
The model performance represented by left confusion matrix indicates that the model has weak positive recognition rate while the right confusion matrix represents that the model has strong positive recognition rate. Note that the accuracy is 60% for both the models. Thus, one needs to dig deeper to understand about the model performance given the accuracy metrics.

The accuracy metrics is also not reliable for the models trained on imbalanced or skewed datasets. Take a scenario of dataset with 95% imbalance (95% data is negative class). The accuracy of the classifier will be very high as it will be correctly doing right prediction issuing negative most of the time. A better classifier that actually deals with the class imbalance issue, is likely to have a worse accuracy metrics score. In such scenario of imbalanced dataset, another metrics AUC (the area under ROC curve) is more robust than the accuracy metrics score.

Accuracy metrics does not take into account the relative importance of different types of errors, such as false positives and false negatives. For example, if a model is being used to predict whether a patient has a certain disease, a false positive (predicting that a patient has the disease when they actually do not) may be less severe than a false negative (predicting that a patient does not have the disease when they actually do). In this case, using accuracy as the sole evaluation metric may not provide a clear picture of the model’s performance.

The following are some of the Kaggle competitions which used accuracy as one of the evaluation metrics:

• Cassava Leaf Disease Classification
• Text Normalization Challenge – English Language

What is F1-Score?

F1 score is harmonic mean of precision and recall score. It gives equal weight to both the Precision and Recall for measuring its performance in terms of accuracy thereby making it an alternative to Accuracy metrics (it doesn’t require us to know the total number of observations). It’s often used as a single value that provides high-level information about the model’s output quality. This is a useful measure of the model in the scenarios where one tries to optimize either of precision or recall score and as a result, the model performance suffers. Here is an example of Kaggle competition which used F1-score as the evaluation metrics: Quora Insincere Questions Classification

The following represents the aspects relating to issues with optimizing either precision or recall score:

• Optimizing for recall helps with minimizing the chance of not detecting a malignant cancer. However, this comes at the cost of predicting malignant cancer in patients although the patients are healthy (a high number of FP).
• Optimize for precision helps with correctness if the patient has malignant cancer. However, this comes at the cost of missing malignant cancer more frequently (a high number of FN).

The following is the formula of F1 Score:

F1 Score = 2* Precision Score * Recall Score/ (Precision Score + Recall Score)

The accuracy score from the above confusion matrix will come out to be the following:

F1 score = (2 * 0.968* 0.968) / (0.968+ 0.968) = 1.874 / 1.936 = 0.968

How to calculate F1-score in Python?

The same score can be obtained by using f1_score method from sklearn.metrics

print('F1 Score: %.3f' % f1_score(y_test, y_pred))

Frequently Asked Questions (FAQs)

The following are some of the most frequently asked questions related to precision, recall, accuracy and F1-score.

• What is difference between recall and precision score?
  • Recall score measures the proportion of actual positive cases correctly identified by a model, focusing on minimizing false negatives. Precision score, on the other hand, measures the proportion of positive identifications that were actually correct, aiming to minimize false positives. In summary, recall score is about capturing as many positives as possible, while precision score is about being accurate in the positives that are identified.
• When is precision more important than recall score?
  • Precision score is more important than recall in scenarios where the cost of false positives is high. For example, in spam detection, it’s crucial to avoid misclassifying legitimate emails as spam. In medical testing, a false positive might lead to unnecessary, invasive procedures. In these cases, it’s preferable to have a highly accurate model that confidently identifies true positives, even if it misses some positive cases, rather than wrongly classifying negatives as positives.
• What are good precision and recall values or scores?
  • Good precision and recall values depend on the specific application and the balance between the cost of false positives and false negatives. In some contexts, like medical diagnoses or fraud detection, high precision is crucial to avoid false alarms. In others, like safety monitoring systems, high recall is more important to ensure no threats are missed. Ideally, both should be as high as possible, but a value above 0.5 is often considered acceptable, and values closer to 1 are excellent. The acceptable threshold varies greatly depending on the specific needs and tolerances of the task at hand.

Conclusions

Here is the summary of what you learned in relation to precision, recall, accuracy, and f1-score.

• A precision score is used to measure the model performance in measuring the count of true positives in the correct manner out of all positive predictions made.
• Recall score is used to measure the model performance in terms of measuring the count of true positives in a correct manner out of all the actual positive values.
• Precision-Recall score is a useful measure of success of prediction when the classes are very imbalanced. 
• Accuracy score is used to measure the model performance in terms of measuring the ratio of sum of true positive and true negatives out of all the predictions made.
• F1-score is used in the scenario where choosing either of precision or recall score can result in compromise in terms of model giving high false positives and false negatives respectively.

Take a Quiz

Results

• Author
• Recent Posts

Follow me

Ajitesh Kumar

I have been recently working in the area of Data analytics including Data Science and Machine Learning / Deep Learning. I am also passionate about different technologies including programming languages such as Java/JEE, Javascript, Python, R, Julia, etc, and technologies such as Blockchain, mobile computing, cloud-native technologies, application security, cloud computing platforms, big data, etc. For latest updates and blogs, follow us on Twitter. I would love to connect with you on Linkedin.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com

Follow me

Latest posts by Ajitesh Kumar (see all)

• Mean Squared Error vs Cross Entropy Loss Function - April 28, 2024
• Cross Entropy Loss Explained with Python Examples - April 28, 2024
• Logistic Regression in Machine Learning: Python Example - April 26, 2024

• Author
• Recent Posts

Follow me

Ajitesh Kumar

I have been recently working in the area of Data analytics including Data Science and Machine Learning / Deep Learning. I am also passionate about different technologies including programming languages such as Java/JEE, Javascript, Python, R, Julia, etc, and technologies such as Blockchain, mobile computing, cloud-native technologies, application security, cloud computing platforms, big data, etc. For latest updates and blogs, follow us on Twitter. I would love to connect with you on Linkedin.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com

Follow me

Latest posts by Ajitesh Kumar (see all)

• Mean Squared Error vs Cross Entropy Loss Function - April 28, 2024
• Cross Entropy Loss Explained with Python Examples - April 28, 2024
• Logistic Regression in Machine Learning: Python Example - April 26, 2024

#1. Which of the following metrics is used to measure the proportion of true positive predictions in a classification model?

Precision

Precision

Recall

Recall

F1 Score

F1 Score

Accuracy

Accuracy

#2. How can one measure the tradeoff between false positives and false negatives within a predictive model?

By calculating the accuracy of the model

By calculating the accuracy of the model

By measuring the precision of the model

By measuring the precision of the model

By monitoring the rate of false positives within the model predictions

By monitoring the rate of false positives within the model predictions

By computing both precision and recall scores for the model

By computing both precision and recall scores for the model

#3. What kind of metric is used to quantify how well a classifier correctly identifies positive instances?

Acccuracy

Acccuracy

Precision

Precision

Recall

Recall

F1-score

F1-score

#4. What is accuracy in machine learning?

A measure of how well a model can predict the desired outcome

A measure of how well a model can predict the desired outcome

A measure of how accurately a model can classify data into different classes

A measure of how accurately a model can classify data into different classes

A measure of the number of correctly predicted results when compared to the total number of predictions

A measure of the number of correctly predicted results when compared to the total number of predictions

A measure of how quickly a model can find patterns in data

A measure of how quickly a model can find patterns in data

#5. How does F1-score help evaluate machine learning models?

It is used to measure prediction accuracy.

It is used to measure prediction accuracy.

It is used to judge whether a given model is suitable for a specific task or not.

It is used to judge whether a given model is suitable for a specific task or not.

It combines precision and recall into one single metric, allowing us to see an overall performance score for our models.

It combines precision and recall into one single metric, allowing us to see an overall performance score for our models.

#6. If you want to measure the ability of a machine learning model to avoid false positives, which metric should you use?

Accuracy

Accuracy

Precision

Precision

Recall

Recall

F1-score

F1-score

#7. What is recall in machine learning?

Recall is a measure of how often a model correctly identifies all relevant items in comparison to the actual number of relevant items present.

Recall is a measure of how often a model correctly identifies all relevant items in comparison to the actual number of relevant items present.

Recall measures how accurate predictions are, based on comparing them to the actual number of relevant items present in a data set.

Recall measures how accurate predictions are, based on comparing them to the actual number of relevant items present in a data set.

Recall evaluates the performance of an algorithm by measuring which instances it was able to identify as belonging to certain classes compared to all instances that should have been identified as belonging to those classes

Recall evaluates the performance of an algorithm by measuring which instances it was able to identify as belonging to certain classes compared to all instances that should have been identified as belonging to those classes

#8. What does higher precision mean when evaluating ML models?

Higher precision means that there are fewer false positives when making predictions with the model, meaning more accurate results overall.

Higher precision means that there are fewer false positives when making predictions with the model, meaning more accurate results overall.

Higher precision means that more predictions are correct when making predictions with the model, leading to better overall results.

Higher precision means that more predictions are correct when making predictions with the model, leading to better overall results.

Higher precision means that less data has been misclassified when making predictions with the model, leading to improved classification accuracy

Higher precision means that less data has been misclassified when making predictions with the model, leading to improved classification accuracy

#9. When is precision more important than recall?

When the cost associated with false positives is high

When the cost associated with false positives is high

When the cost associated with false negatives is low

When the cost associated with false negatives is low

When both types of errors have equal costs

When both types of errors have equal costs

#10. What are some ways to optimize accuracy metrics for a given model?

Use feature selection methods to eliminate irrelevant data points and variables from your dataset

Use feature selection methods to eliminate irrelevant data points and variables from your dataset

Employ regularization techniques like L1, L2, or dropout to control overfitting

Employ regularization techniques like L1, L2, or dropout to control overfitting

Adjust hyperparameters such as learning rate or optimization algorithm to tweak model performance parameters

Adjust hyperparameters such as learning rate or optimization algorithm to tweak model performance parameters

All of the Above

All of the Above

#11. Which of the following metrics is used to measure the proportion of true positive predictions out of all actual positive instances in a classification model?

Accuracy

Accuracy

Precision

Precision

Recall

Recall

F1-Score

F1-Score

#12. In a classification model, a high precision value indicates:

A high proportion of true positive predictions

A high proportion of true positive predictions

A low proportion of false positive predictions

A low proportion of false positive predictions

Both a and b

Both a and b

#13. Which of the following metrics is used to balance precision and recall in a classification model?

Precision

Precision

Recall

Recall

F1-Score

F1-Score

#14. In a binary classification problem, a trade-off between precision and recall can occur when:

Lowering the threshold for positive predictions increases recall but decreases precision

Lowering the threshold for positive predictions increases recall but decreases precision

Increasing the threshold for positive predictions increases precision but decreases recall

Increasing the threshold for positive predictions increases precision but decreases recall

Both of the above

Both of the above

Finish

• Author
• Recent Posts

Follow me

Ajitesh Kumar

I have been recently working in the area of Data analytics including Data Science and Machine Learning / Deep Learning. I am also passionate about different technologies including programming languages such as Java/JEE, Javascript, Python, R, Julia, etc, and technologies such as Blockchain, mobile computing, cloud-native technologies, application security, cloud computing platforms, big data, etc. For latest updates and blogs, follow us on Twitter. I would love to connect with you on Linkedin.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com

Follow me

Latest posts by Ajitesh Kumar (see all)

• Mean Squared Error vs Cross Entropy Loss Function - April 28, 2024
• Cross Entropy Loss Explained with Python Examples - April 28, 2024
• Logistic Regression in Machine Learning: Python Example - April 26, 2024