In this post, you will learn about the concepts of Perceptron with the help of Python example. It is very important for data scientists to understand the concepts related to Perceptron as a good understanding lays the foundation of learning advanced concepts of neural networks including deep neural networks (deep learning).
What is Perceptron?
Perceptron is a machine learning algorithm which mimics how a neuron in the brain works. It is also called as single layer neural network consisting of a single neuron. The output of this neural network is decided based on the outcome of just one activation function associated with the single neuron. In perceptron, the forward propagation of information happens. Deep neural network consists of one or more perceptrons laid out in two or more layers. Input to different perceptrons in a particular layer will be fed from previous layer by combining them with different weights.
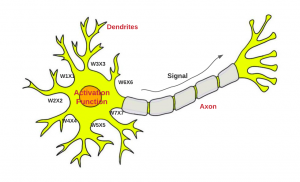
Let’s first understand how a neuron works. The diagram below represents a neuron in the brain. The input signals (x1, x2, …) of different strength (observed weights, w1, w2 …) is fed into the neuron cell as weighted sum via dendrites. The weighted sum is termed as the net input. The net input is processed by the neuron and output signal (observer signal in AXON) is appropriately fired. In case the combined signal strength is not appropriate based on decision function within neuron cell (observe activation function), the neuron does not fire any output signal.
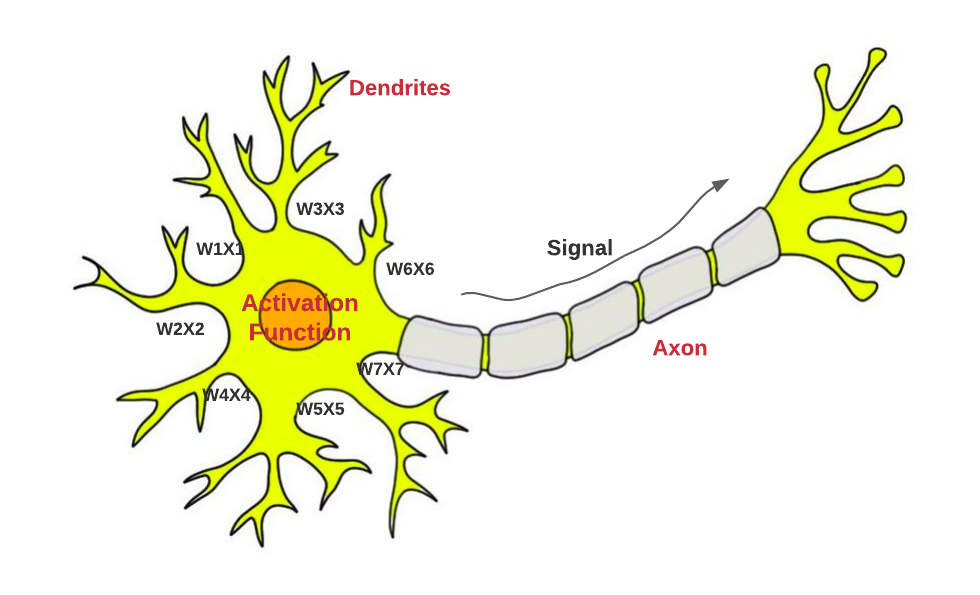
The following is an another view of understanding an artificial neuron, a perceptron, in relation to a biological neuron from the viewpoint of how input and output signals flows:
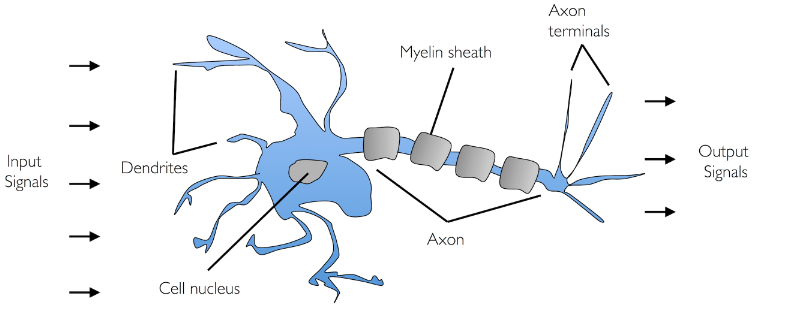
The perceptron when represented as line diagram would look like the following with mathematical notations:
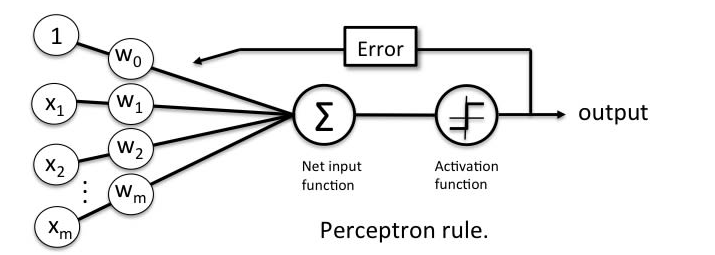
Pay attention to some of the following in relation to what’s shown in the above diagram representing a neuron:
- Step 1 – Input signals weighted and combined as net input: Weighted sums of input signal reaches to the neuron cell through dendrites. The weighted inputs does represent the fact that different input signal may have different strength, and thus, weighted sum. This weighted sum can as well be termed as net input to the neuron cell.
- Step 2 – Net input fed into activation function: Weighted The weighted sum of inputs or net input is fed as input to what is called as activation function. The activation function is a non-linear activation function. The activation functions are of different types such as the following:
- Unit step function
- Sigmoid function (Popular one as it outputs number between 0 and 1 and thus can be used to represent probability)
- Rectilinear (ReLU) function
- Hyperbolic tangent
The diagram below depicts different types of non-linear activation functions.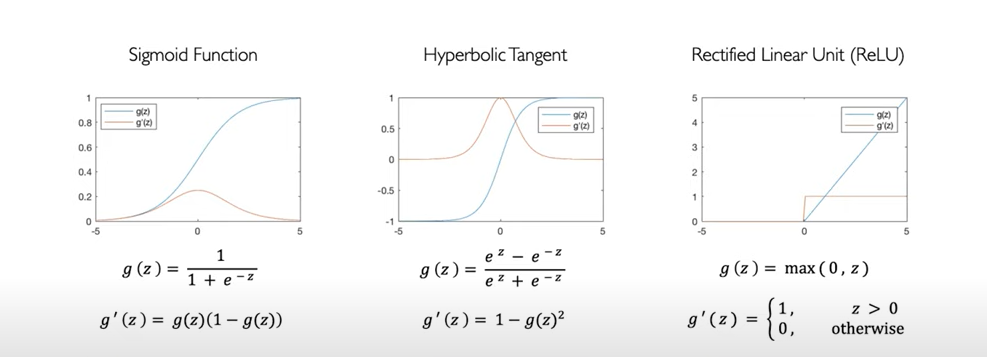
- Step 3A – Activation function outputs binary signal appropriately: The activation function processes the net input based on the unit step (Heaviside) function and outputs the binary signal appropriately as either 1 or 0. The activation function for perceptron can be said to be a unit step function. Recall that the unit step function, u(t), outputs the value of 1 when t >= 0 and 0 otherwise. In the case of a shifted unit step function, the function u(t-a) outputs the value of 1 when t >= a and 0 otherwise.
- Step 3B – Learning input signal weights based on prediction vs actuals: A parallel step is a neuron sending the feedback to strengthen the input signal strength (weights) appropriately such that it could create an output signal appropriately that matches the actual value. The feedback is based on the outcome of the activation function which is a unit step function. Weights are updated based on the gradient descent learning algorithm. Here is my post on gradient descent – Gradient descent explained simply with examples. Here is the equation based on which the weights get updated:
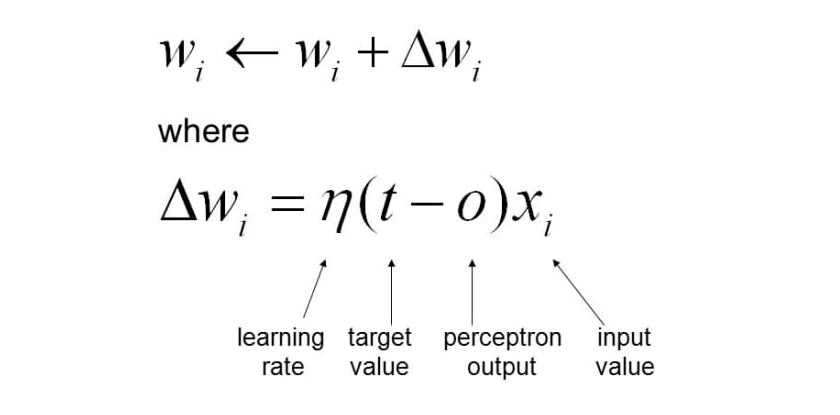
Pay attention to some of the following in above equation vis-a-vis Perceptron learning algorithm:
- Weights get updated by [latex]\delta w[/latex]
- [latex]\delta w[/latex] is derived by taking the first-order derivative of the loss function (gradient) and multiplying the output with negative (gradient descent) of learning rate. The output is what is shown in the above equation – the product of learning rate, the difference between actual and predicted value (perceptron output), and input value.
- In this post, the weights are updated based on each training example such that the perceptron can learn to predict closer to the actual output for the next input signal. This is also called stochastic gradient descent (SGD). Here is my post on stochastic gradient descent. That said, one could also try batch gradient descent to learn the weights of input signals.
Here is another picture of Perceptron that represents the concept explained above.
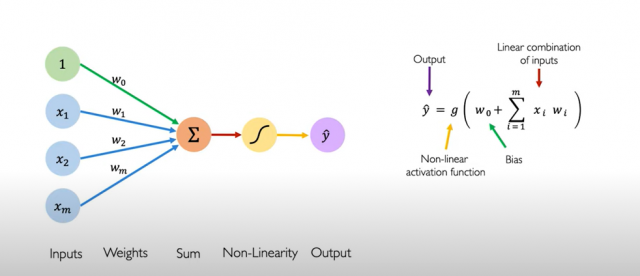
Perceptron Python Code Example
In this section, we will look each of the steps described in previous section and understand the implementation with the Python code:
- Input signals weighted and combined as net input: Input signals get multiplied with weights and the sum of all weighted input signal is taken. This sum is called as net input and would be fed into activation function. Here is the code for net input. Note the dot product of coefficients with input X. Coefficient[0] is multiplied with 1 (bias element).
'''
Net Input is sum of weighted input signals
'''
def net_input(self, X):
weighted_sum = np.dot(X, self.coef_[1:]) + self.coef_[0]
return weighted_sum
- Activation function invoked with net input: Net input is fed into activation function and output is determined based on the outcome of unit step function. Here is the code:
'''
Activation function is fed the net input and the unit step function is executed to determine the output.
'''
def activation_function(self, X):
weighted_sum = self.net_input(X)
return np.where(weighted_sum >= 0.0, 1, 0)
- Prediction based on the activation function output: In Perceptron, the prediction output coincides with (or equal to ) the output of activation function which uses unit step function. This is where the Perceptron is different from ADAptive LInear NEuron also termed as Adaline. The Adaline algorithm implementation will be described in future post. In Adaline algorithm, the activation function is identity function and prediction is done based on unit step function output.
'''
Prediction is made on the basis of output of activation function
'''
def predict(self, X):
return self.activation_function(X)
- Learning weights based on the prediction vs actual: Weights are learned based on comparing the value of actual label and the predicted label (binary) and applying stochastic gradient descent algorithm to learn weights based on each training example. The idea is to improve on making predictions based on the learning from last training example. Here is the fit method which demonstrates the learning of input weights:
'''
Stochastic Gradient Descent
1. Weights are updated based on each training examples.
2. Learning of weights can continue for multiple iterations
3. Learning rate needs to be defined
'''
def fit(self, X, y):
rgen = np.random.RandomState(self.random_state)
self.coef_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
for _ in range(self.n_iterations):
for xi, expected_value in zip(X, y):
predicted_value = self.predict(xi)
self.coef_[1:] = self.coef_[1:] + self.learning_rate * (expected_value - predicted_value) * xi
self.coef_[0] = self.coef_[0] + self.learning_rate * (expected_value - predicted_value) * 1
Here is how the entire Python code for Perceptron implementation would look like. This implementation is used to train the binary classification model that could be used to classify the data in one of the binary classes. Pay attention to all the methods that are explained previously. Also, pay attention to the score method which is used to measure the accuracy of the model.
import numpy as np
#
# Perceptron implementation
#
class CustomPerceptron(object):
def __init__(self, n_iterations=100, random_state=1, learning_rate=0.01):
self.n_iterations = n_iterations
self.random_state = random_state
self.learning_rate = learning_rate
'''
Stochastic Gradient Descent
1. Weights are updated based on each training examples.
2. Learning of weights can continue for multiple iterations
3. Learning rate needs to be defined
'''
def fit(self, X, y):
rgen = np.random.RandomState(self.random_state)
self.coef_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
self.errors_ = []
for _ in range(self.n_iterations):
errors = 0
for xi, expected_value in zip(X, y):
predicted_value = self.predict(xi)
self.coef_[1:] = self.coef_[1:] + self.learning_rate * (expected_value - predicted_value) * xi
self.coef_[0] = self.coef_[0] + self.learning_rate * (expected_value - predicted_value) * 1
update = self.learning_rate * (expected_value - predicted_value)
errors += int(update != 0.0)
self.errors_.append(errors)
'''
Net Input is sum of weighted input signals
'''
def net_input(self, X):
weighted_sum = np.dot(X, self.coef_[1:]) + self.coef_[0]
return weighted_sum
'''
Activation function is fed the net input and the unit step function
is executed to determine the output.
'''
def activation_function(self, X):
weighted_sum = self.net_input(X)
return np.where(weighted_sum >= 0.0, 1, 0)
'''
Prediction is made on the basis of output of activation function
'''
def predict(self, X):
return self.activation_function(X)
'''
Model score is calculated based on comparison of
expected value and predicted value
'''
def score(self, X, y):
misclassified_data_count = 0
for xi, target in zip(X, y):
output = self.predict(xi)
if(target != output):
misclassified_data_count += 1
total_data_count = len(X)
self.score_ = (total_data_count - misclassified_data_count)/total_data_count
return self.score_
Here is the Python code which could be used to train the model using CustomPerceptron algorithm shown above. Note that SKlean breast cancer data is used for training the model in order to classify / predict the breast cancer.
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
#
# Load the data set
#
bc = datasets.load_breast_cancer()
X = bc.data
y = bc.target
#
# Create training and test split
#
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
#
# Instantiate CustomPerceptron
#
prcptrn = CustomPerceptron(n_iterations=10)
#
# Fit the model
#
prcptrn.fit(X_train, y_train)
#
# Score the model
#
prcptrn.score(X_test, y_test), prcptrn.score(X_train, y_train)
Executing the above code will print the accuracy score with test and training data set. (0.8888888888888888, 0.9120603015075377
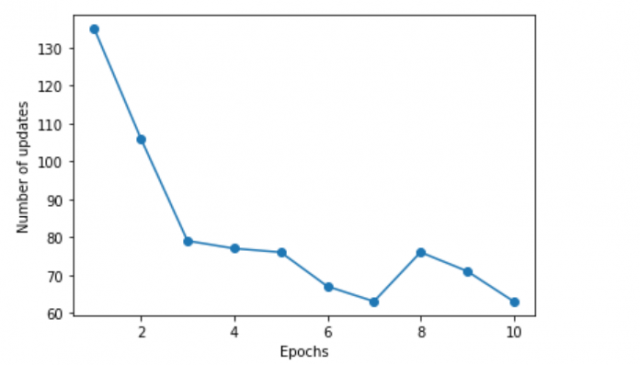
The code below plots the error vs Epochs. Epoch is a machine learning term used to describe the point at which a model has seen all of the training data once. Training data is fed into the model during Epochs. The number of Epochs is a hyperparameter that can be tuned to improve model performance. Generally, more Epochs will result in better performance, but at the expense of longer training time. When working with large datasets, it is common to run for hundreds or even thousands of Epochs. However, it is important to monitor the model closely to ensure that it is not overfitting the training data.
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(range(1, len(prcptrn.errors_) + 1), prcptrn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of updates')
# plt.savefig('images/02_07.png', dpi=300)
plt.show()
The following plot representing errors vs Epochs will be printed.
Sklearn.linear_model Perceptron Example
The following Python code represents usage of Perceptron classifier from Sklearn.linear_model package.
from sklearn import datasets
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Perceptron
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=1, stratify=y)
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
ppn = Perceptron(eta0=0.1, random_state=1)
ppn.fit(X_train_std, y_train)
y_pred = ppn.predict(X_test_std)
print('Accuracy: %.3f' % accuracy_score(y_test, y_pred))
print('Accuracy: %.3f' % ppn.score(X_test_std, y_test))
Conclusions
Here is the summary of what you learned about the Perceptron algorithm with help of Python implementation:
- Perceptron mimics the neuron in the human brain
- Perceptron is termed as machine learning algorithm as weights of input signals are learned using the algorithm
- Perceptron algorithm learns the weight using gradient descent algorithm. Both stochastic gradient descent and batch gradient descent could be used for learning the weights of the input signals
- The activation function of Perceptron is based on the unit step function which outputs 1 if the net input value is greater than or equal to 0, else 0.
- The prediction is also based on the unit step function.
- The Watermelon Effect: When Green Metrics Lie - January 25, 2026
- Coefficient of Variation in Regression Modelling: Example - November 9, 2025
- Chunking Strategies for RAG with Examples - November 2, 2025

Muy buenos