In this post, you will learn the concepts of Stochastic Gradient Descent (SGD) using a Python example. Stochastic gradient descent is an optimization algorithm that is used to optimize the cost function while training machine learning models. The most popular algorithm such as gradient descent takes a long time to converge for large datasets. This is where the variant of gradient descent such as stochastic gradient descent comes into the picture. In order to demonstrate Stochastic gradient descent concepts, the Perceptron machine learning algorithm is used. Recall that Perceptron is also called a single-layer neural network. Before getting into details, let’s quickly understand the concepts of Perceptron and the underlying learning algorithm such as SGD is used. You may want to check out the concepts of gradient descent on this page – Gradient Descent explained with examples.
What’s Stochastic Gradient Descent?
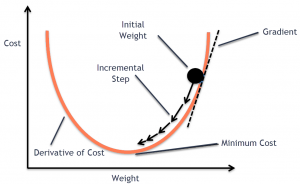
Stochastic gradient descent (SGD) is a type of optimization algorithm used in machine learning. It is one of the most popular algorithms, due to its simplicity and efficiency. It is an iterative algorithm, which means that it goes through the training data multiple times, each time making small adjustments to the model parameters in order to minimize the error. SGD is a “stochastic” algorithm because it randomly selects one training example at each iteration, as opposed to using the entire training set as some other algorithms do. SGD works by making small, random updates to the parameters of a model, in order to find the values that minimize a cost function. The advantage of SGD over other optimization algorithms is that it can be used on very large datasets, and it typically converges faster than other algorithms. Another advantage of SGD is that it is relatively easy to implement, which has made it one of the most popular learning. SGD is also efficient in terms of storage, as only a small number of samples need to be stored in memory at each iteration.
Here is the Python code which represents the learning of weights (or weight updation) after each training example. Pay attention to the following in order to understand how Stochastic gradient descent works:
- The fit method runs multiple iterations of the process of learning weights. This is assigned using n_iterations.
- In each iteration, each of the training examples is used for updating the weights. Notice the code for xi, target in zip(X, y)
- The delta value which needs to be updated to weights is calculated as the multiplication of the learning rate (set as 0.01), the difference between the expected value and predicted value, and feature values. Note that the predicted value is calculated based on the comparison of the output of the activation function with 0. If the comparison is greater than 0, the prediction is 1 otherwise 0.
- Weights get updated with the delta value calculated in the previous step.
- New weights get applied with the next training example.
- Step 2, 3, 4, and 5 is what is called stochastic gradient descent.
n_iterations = 100
learning_rate = 0.01
def predict(X, y, coef):
'''
Activation function: w0 + w1*x1 + w2*x2 + ... + wn*xn
'''
output = np.dot(X, coef[1:]) + coef[0]
'''
Unit Step function: Predict 1 if output >= 0 else 0
'''
return np.where(output >= 0.0, 1, 0)
def fit(X, y):
rgen = np.random.RandomState(1)
coef_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
for _ in range(n_iterations):
for xi, expected_value in zip(X, y):
predicted_value = predict(xi, target, coef_)
coef_[1:] += learning_rate * (expected_value - predicted_value) * xi
coef_[0] += learning_rate * (expected_value - predicted_value) * 1
return coef_
Perceptron Python Code representing SGD
Here is the Perceptron code representing stochastic gradient descent algorithm implementation. Pay attention to fit method which consists of the same code as described in the previous section.
class CustomPerceptron(object):
def __init__(self, n_iterations=100, random_state=1, learning_rate=0.01):
self.n_iterations = n_iterations
self.random_state = random_state
self.learning_rate = learning_rate
'''
Stochastic Gradient Descent
1. Weights are updated based on each training examples.
2. Learning of weights can continue for multiple iterations
3. Learning rate needs to be defined
'''
def fit(self, X, y):
rgen = np.random.RandomState(self.random_state)
self.coef_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
for _ in range(self.n_iterations):
for xi, expected_value in zip(X, y):
predicted_value = self.predict(xi)
self.coef_[1:] += self.learning_rate * (expected_value - predicted_value) * xi
self.coef_[0] += self.learning_rate * (expected_value - predicted_value) * 1
'''
Activation function calculates the value of weighted sum of input value
'''
def activation(self, X):
return np.dot(X, self.coef_[1:]) + self.coef_[0]
'''
Prediction is made on the basis of unit step function
'''
def predict(self, X):
output = self.activation(X)
return np.where(output >= 0.0, 1, 0)
'''
Model score is calculated based on comparison of
expected value and predicted value
'''
def score(self, X, y):
misclassified_data_count = 0
for xi, target in zip(X, y):
output = self.predict(xi)
if(target != output):
misclassified_data_count += 1
total_data_count = len(X)
self.score_ = (total_data_count - misclassified_data_count)/total_data_count
return self.score_
You could use the following code to train a model using CustomPerceptron implementation and calculate the score. Note the Sklearn Breast cancer data set is used for training the model.
#
# Load the data set
#
bc = datasets.load_breast_cancer()
X = bc.data
y = bc.target
#
# Create training and test split
#
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
#
# Instantiate CustomPerceptron
#
prcptrn = CustomPerceptron()
#
# Fit the model
#
prcptrn.fit(X_train, y_train)
#
# Score the model
#
prcptrn.score(X_test, y_test), prcptrn.score(X_train, y_train)
Stochastic Gradient Descent (SGD) for Learning Perceptron Model
Perceptron algorithm can be used to train a binary classifier that classifies the data as either 1 or 0. It is based on the following:
- Gather data: First and foremost, one or more features get defined. Thereafter, the data for those features is collected along with the class label representing the binary class of each record.
- Invoke activation function: A function called as activation function is invoked which sums up the weighted sum of input data. The weighted sum represent the sum of different weights, [latex]w_i[/latex] with different features, [latex]x_i[/latex]. This is the formula: [latex]\sum w_i*x_i[/latex]. In the weighted sum, [latex]x_0[/latex] = 1
- Use unit step function to predict class 0 or 1: The output of the activation function is compared with 0. If the output is greater than or equal to 0, the prediction is 1 or else the prediction is 0.
In order to achieve the above, what is unknown is weights which are also called coefficients in the case of linear regression. And, the weights are entities that need to be learned as part of training or fitting the model. In other words, the model is trained with the data set to learn weights or parameters, or coefficients. The algorithm which is used to learn the weights is called stochastic gradient descent.
What are the advantages of using Stochastic Gradient Descent (SGD) for learning weights?
Here are a couple of advantages of using SGD for learning model parameters (not hyperparameters) or weights.
- SGD helps the model to converge fast empirically in the case of large training data set
- Using SGD, one can achieve better generalization when using the model for predicting population or unseen data sets.
Conclusions
Here is the summary of what you learned in relation to stochastic gradient descent along with Python implementation and related examples:
- Stochastic gradient descent (SGD) is a gradient descent algorithm used for learning weights/parameters/coefficients of the model, be it perceptron or linear regression.
- SGD requires updating the weights of the model based on each training example.
- SGD is particularly useful when there are large training data set.
- Models trained using an algorithm which applies the stochastic gradient descent algorithm for learning weights is found to generalize better on an unseen data set.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me