Micro-average, Macro-average, Weighting: Precision, Recall, F1-Score

Last updated: 30th Dec, 2023

In this post, you will learn about how to use micro-averaging and macro-averaging methods for evaluating scoring metrics (precision, recall, f1-score) for multi-class classification machine learning problem. You will also learn about weighting method used as one of the other averaging choices of metrics such as precision, recall and f1-score for multi-class classification problem. The concepts will be explained with Python code examples. 

What & Why of Micro, Macro-averaging and Weighting metrics?

Micro and macro-averaging methods are used in the evaluation of classification models, to compute performance metrics like precision, recall, and F1-score. These methods are especially relevant in scenarios involving multi-class or multi-label classification. In case of multi-class classification, micro and macro-averaging help understand model performance across all these classes, especially important when some classes are more common than others. In case of multi-label classification, micro-averaging becomes crucial in understanding the overall performance across all labels, while macro-averaging shows how well the model performs on each label independently.

Weighted averaging is a method where each class’s metric is multiplied by a weight that reflects its importance or prevalence in the dataset. The weighted average is then calculated by summing these weighted metrics. The idea is to balance the influence of each class on the overall metric, especially in cases where classes are imbalanced (i.e., some classes have more instances than others). While micro-averaging treats every instance equally, regardless of the class, weighted averaging adjusts the metric based on the class frequency, giving a middle ground between treating every instance equally (micro-averaging) and every class equally (macro-averaging). Unlike macro-averaging, which computes the average metric across classes without considering class frequency, weighted averaging accounts for class frequency by adjusting the influence of each class on the overall metric.

Formula for Micro-averaging, Macro-averaging and Weighted Averaging

Here is the formula for all the three methods:

• Precision (Micro-Averaged)

  • $\Large \text{Precision}_{\text{micro}} = \frac{\sum_{i=1}^{n} \text{TP}_i}{\sum_{i=1}^{n} (\text{TP}_i + \text{FP}_i)} $

• Precision (Macro-Averaged)

  • $\Large \text{Precision}_{\text{macro}} = \frac{1}{n} \sum_{i=1}^{n} \left( \frac{\text{TP}_i}{\text{TP}_i + \text{FP}_i} \right) $

• Precision (Weighted Averaged)

  • $\Large \text{Precision}_{\text{weighted}} = \sum_{i=1}^{n} w_i \left( \frac{\text{TP}_i}{\text{TP}_i + \text{FP}_i} \right) $
  • where $w_i$ is the weight for class $i$.

• Recall (Micro-Averaged)

  • $\Large \text{Recall}_{\text{micro}} = \frac{\sum_{i=1}^{n} \text{TP}_i}{\sum_{i=1}^{n} (\text{TP}_i + \text{FN}_i)} $

• Recall (Macro-Averaged)

  • $\Large \text{Recall}_{\text{macro}} = \frac{1}{n} \sum_{i=1}^{n} \left( \frac{\text{TP}_i}{\text{TP}_i + \text{FN}_i} \right) $

• Recall (Weighted Averaged)

  • $\Large \text{Recall}_{\text{weighted}} = \sum_{i=1}^{n} w_i \left( \frac{\text{TP}_i}{\text{TP}_i + \text{FN}_i} \right) $

• F1-Score (Micro-Averaged)

  • $\Large \text{F1}_{\text{micro}} = \frac{2 \times \sum_{i=1}^{n} \text{TP}_i}{2 \times \sum_{i=1}^{n} \text{TP}_i + \sum_{i=1}^{n} \text{FP}_i + \sum_{i=1}^{n} \text{FN}_i} $

• F1-Score (Macro-Averaged)

  • $\Large \text{F1}_{\text{macro}} = \frac{1}{n} \sum_{i=1}^{n} \left( 2 \times \frac{\frac{\text{TP}_i}{\text{TP}_i + \text{FP}_i} \times \frac{\text{TP}_i}{\text{TP}_i + \text{FN}_i}}{\frac{\text{TP}_i}{\text{TP}_i + \text{FP}_i} + \frac{\text{TP}_i}{\text{TP}_i + \text{FN}_i}} \right) $

• F1-Score (Weighted Averaged)

  • $\Large \text{F1}_{\text{weighted}} = \sum_{i=1}^{n} w_i \left( 2 \times \frac{\frac{\text{TP}_i}{\text{TP}_i + \text{FP}_i} \times \frac{\text{TP}_i}{\text{TP}_i + \text{FN}_i}}{\frac{\text{TP}_i}{\text{TP}_i + \text{FP}_i} + \frac{\text{TP}_i}{\text{TP}_i + \text{FN}_i}} \right) $

When to use Micro-averaging, Macro-averaging & Weighting scores?

Use micro-averaging score when there is a need to weight each instance or prediction equally.

Use macro-averaging score when all classes need to be treated equally to evaluate the overall performance of the classifier with regard to the most frequent class labels.

Use weighted macro-averaging score in case of class imbalances (different number of instances related to different class labels). The weighted macro-average is calculated by weighting the score of each class label by the number of true instances when calculating the average.

Python Examples for Micro-averaging & Macro-averaging Methods

Here is the Python code sample representing the calculation of micro-average and macro-average precision & recall score for model trained on SkLearn IRIS dataset which has three different classes namely, setosa, versicolor, virginica. In order to create a confusion matrix having numbers across all the cells, only one feature is used for training the model. Pay attention to the training data X assigned to iris.data[:, [1]]. 

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.pipeline import make_pipeline
import matplotlib.pyplot as plt
from sklearn.metrics import precision_score
#
# Load the data set
#
iris = datasets.load_iris()
X = iris.data[:, [1]]
y = iris.target
#
# Create the training and test split
#
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=1, stratify=y)
#
# Create a pipeline
#
pipeline = make_pipeline(StandardScaler(), RandomForestClassifier(random_state=1))
#
# Fit the estimator , pipeline
#
pipeline.fit(X_train, y_train)
#
# Get the predictions
#
y_pred = pipeline.predict(X_test)
#
# Calculate the confusion matrix
#
conf_matrix = confusion_matrix(y_test, y_pred)
#
# Print the confusion matrix using Matplotlib
#
fig, ax = plt.subplots(figsize=(6, 6))
ax.matshow(conf_matrix, cmap=plt.cm.Oranges, alpha=0.3)
for i in range(conf_matrix.shape[0]):
    for j in range(conf_matrix.shape[1]):
        ax.text(x=j, y=i,s=conf_matrix[i, j], va='center', ha='center', size='xx-large')

plt.xlabel('Predicted', fontsize=18)
plt.ylabel('Actuals', fontsize=18)
plt.title('Confusion Matrix', fontsize=18)
plt.show()

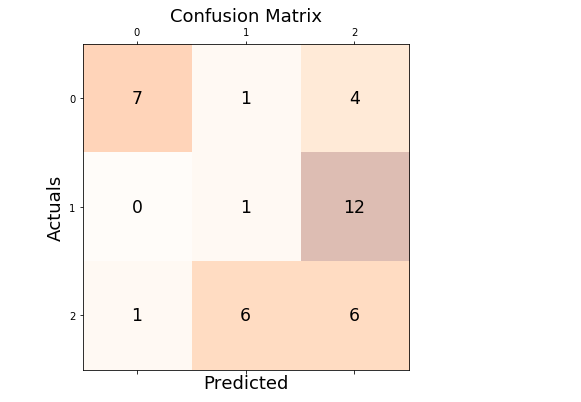
This is how the confusion matrix would look like with model trained on IRIS data set with just one feature.

Here is how the Python code looks like for measuring the micro-average and macro-average precision scores:

# True positives prediction (diagonally) for all the classes
#
TP = 7 + 1 + 6
#
# False positives for all the classes
#
FP = 1 + 4 + 0 + 12 + 1 + 6
#
# Micro-average precision scores for all the classes
#
precisionScore_manual_microavg = TP / (TP + FP)
# 
# Macro-average of precision scores of all the classes
#
precisionScore_manual_macroavg = ((7/8) + (1/8) + (6/22))/3 
#
# Print the micro-average and macro-average precision scores
#
precisionScore_manual_microavg, precisionScore_manual_macroavg

The same can as well be calculated using Sklearn precision_score, recall_score and f1-score methods. The parameter “average” need to be passed micro, macro and weighted to find micro-average, macro-average and weighted average scores respectively. Here is the sample code:

#
# Average is assigned micro
#
precisionScore_sklearn_microavg = precision_score(y_test, y_pred, average='micro')
#
# Average is assigned macro
#
precisionScore_sklearn_macroavg = precision_score(y_test, y_pred, average='macro')
#
# Printing micro and macro average precision score
#
precisionScore_sklearn_microavg, precisionScore_sklearn_macroavg

Conclusions

Here is what you learned about the micro-averaging and macro-averaging scoring metrics in relation to multi-class classification problem.

• Micro-averaging and macro-averaging scoring metrics is used for evaluating models trained for multi-class classification problems.
• Macro-averaging scores are arithmetic mean of individual classes’ score in relation to precision, recall and f1-score
• Micro-averaging precision scores is sum of true positive for individual classes divided by sum of predicted positives for all classes
• Micro-averaging recall scores is sum of true positive for individual classes divided by sum of actual positives for all classes
• Use micro-averaging score when there is a need to weight each instance or prediction equally.
• Use macro-averaging score when all classes need to be treated equally to evaluate the overall performance of the classifier with regard to the most frequent class labels.
• Use weighted macro-averaging score in case of class imbalances (different number of instances related to different class labels).

• Author
• Recent Posts

Ajitesh Kumar

I have been recently working in the area of Data analytics including Data Science and Machine Learning / Deep Learning. I am also passionate about different technologies including programming languages such as Java/JEE, Javascript, Python, R, Julia, etc, and technologies such as Blockchain, mobile computing, cloud-native technologies, application security, cloud computing platforms, big data, etc. I would love to connect with you on Linkedin.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.

Latest posts by Ajitesh Kumar (see all)

• Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
• LLMs for Adaptive Learning & Personalized Education - October 8, 2024
• Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024