As a data scientist, understanding the nuances of various loss functions is critical for building effective machine learning models. Choosing the right loss function can significantly impact the performance of your model and determine how well it generalizes to unseen data. In this blog post, we will delve into two widely used loss functions: Mean Squared Error (MSE) and Cross Entropy Loss. By comparing their properties, applications, and trade-offs, we aim to provide you with a solid foundation for selecting the most suitable loss function for your specific problem.
Loss functions play a pivotal role in training machine learning models as they quantify the difference between the model’s predictions and the actual target values. A well-chosen loss function enables the model to learn from its mistakes and iteratively update its parameters to minimize the error. This ultimately results in more accurate and reliable predictions.
In this post, you will be learning the difference between two common types of loss functions: Cross-Entropy Loss and Mean Squared Error (MSE) Loss, their respective advantages and disadvantages, and their applications in various machine learning tasks. These loss functions are used in machine learning for classification & regression tasks, respectively, to measure how well a model performs on unseen dataset. Whether you are a seasoned data scientist or just starting your journey in the field, mastering the concepts of Mean Squared Error and Cross Entropy Loss is crucial for achieving success in the rapidly evolving world of machine learning.
What is Cross-Entropy Loss?
Cross entropy loss, also known as log loss, is a widely-used loss function in machine learning, particularly for classification problems. It quantifies the difference between the predicted probability distribution and the actual or true distribution of the target classes. Cross entropy loss is often used when training models that output probability estimates, such as logistic regression and neural networks.
The name “cross entropy” for the cross entropy loss function comes from its roots in information theory. In information theory, entropy measures the average amount of “surprise” or uncertainty in a probability distribution. Entropy is used to quantify the randomness or unpredictability of a given distribution. Cross entropy, on the other hand, quantifies the divergence between the two distributions.
Cross entropy loss represents the difference between the predicted probability distribution (Q) produced by the model with the true distribution of the target classes (P). Minimizing cross entropy loss represents the goal of minimizing the divergence or difference between these two distributions. By minimizing the cross entropy loss, the model is encouraged to produce probability estimates that closely match the true class distributions. This results in better predictions and classification performance.
For both binary and multi-class classification problems, the main goal is to minimize the cross entropy loss, which in turn maximizes the likelihood of assigning the correct class labels to the input data points. An example of the usage of cross-entropy loss for multi-class classification problems is training the model using MNIST dataset.
Cross entropy loss for binary classification problem
In a binary classification problem, there are two possible classes (0 and 1) for each data point. The cross entropy loss for binary classification can be defined as:
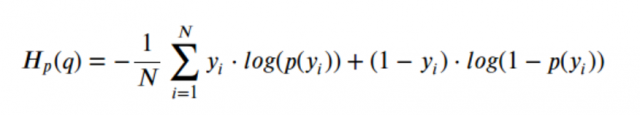
Here, ‘y’ represents the true class label (0 or 1), and ‘p’ represents the predicted probability of the class 1. The loss function penalizes the model more heavily when it assigns a low probability to the true class.
Cross entropy loss for multi-class classification problem
For multi-class classification problems, where there are more than two possible classes, we use the general form of cross entropy loss. Given ‘C’ classes, the multi-class cross entropy loss for a single data point can be defined as:
Here, [latex]y_i[/latex] represents the true class label for class ‘i’ (1 if the true class is ‘i’, 0 otherwise), and [latex]\hat{y_i}[/latex] is the predicted probability of class ‘i’. The summation runs over all the classes. Like in the binary case, the loss function penalizes the model when it assigns low probabilities to the true classes.
A common example used to understand cross-entropy loss is comparing apples and oranges where each fruit has a certain probability of being chosen out of three probabilities (apple, orange, or other). Apple would have an 80% chance while Oranges will only get 20%. In order for our model to make correct predictions in this example, it should assign a high probability to apple and a low for orange. If cross-entropy loss is used, we can compute the cross-entropy loss for each fruit and assign probabilities accordingly. We will then want to choose apple with a higher probability as it has less cross entropy lost than oranges.
What is Mean Squared Error (MSE) Loss?
Mean squared error (MSE) loss is a widely-used loss function in machine learning and statistics that measures the average squared difference between the predicted values and the actual target values. It is particularly useful for regression problems, where the goal is to predict continuous numerical values.
How do you calculate mean squared error loss?
Mean squared error (MSE) loss is calculated by squaring the difference between true value y and the predicted value [latex]\hat{y}[/latex].We take these new numbers (square them), add all of that together to get a final value, finally divide this number by y again. This will be our final result.
The formula for calculating mean squared error loss is as follows:
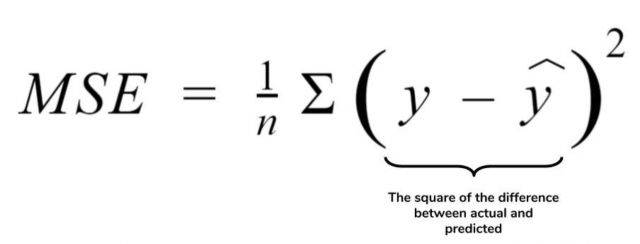
This will give us a loss value between 0 and infinity with larger values indicating mean squared error.
Root mean square error (RMSE) is a mean square error loss function that is normalized between 0 and infinity. The root mean squared error (RMSE) can be written as follows:
$$RMSE = \sqrt{\frac{ mean\_squared\_error}}$$
Machine learning models that often use MSE for training include some of the following:
-
Linear Regression: Linear regression models the relationship between a dependent variable and one or more independent variables. It assumes a linear relationship and tries to fit a straight line that minimizes the MSE between the predicted values and the actual target values.
-
Ridge and Lasso Regression: These are extensions of linear regression that incorporate regularization techniques (L2 for Ridge, L1 for Lasso) to prevent overfitting. The objective function in both cases includes the MSE term along with the regularization term.
-
Decision Trees and Random Forests: For regression tasks, decision trees and random forests can be trained to minimize the MSE at each node. This helps the model to make better predictions by finding the optimal split points in the feature space.
-
Neural Networks: When used for regression problems, neural networks can be trained with MSE as the loss function. By minimizing the MSE, the network learns to predict continuous values that are close to the actual target values.
MSE is a popular choice for training regression models because it is simple, interpretable, and differentiable, which makes it suitable for gradient-based optimization algorithms. However, it may not be the best choice for all situations, as it can be sensitive to outliers and may not handle certain types of distributions well. In such cases, alternative loss functions like Mean Absolute Error (MAE) or Huber loss might be more appropriate.
Conclusion
In this blog post, we have explored the key differences between Mean Squared Error (MSE) and Cross Entropy Loss, two widely-used loss functions in machine learning. Understanding their properties, advantages, and limitations is essential for data scientists to make informed decisions when choosing the most suitable loss function for their specific problem. We have seen that MSE is particularly well-suited for regression tasks, as it quantifies the average squared difference between predicted and actual target values. On the other hand, Cross Entropy Loss is more commonly used in classification problems, where it measures the divergence between the predicted probability distribution and the true distribution of target classes. Selecting the appropriate loss function for your model can significantly impact its performance and ability to generalize to unseen data. By considering the nature of the problem, the distribution of the data, and the desired properties of the model’s predictions, you can choose the loss function that best aligns with your objectives. I hope this blog post has provided valuable insights into the world of loss functions, and thus, would encourage you t continue exploring this fascinating topic. Happy learning!
- Logistic Regression in Machine Learning: Python Example - April 26, 2024
- MSE vs RMSE vs MAE vs MAPE vs R-Squared: When to Use? - April 25, 2024
- Gradient Descent in Machine Learning: Python Examples - April 22, 2024
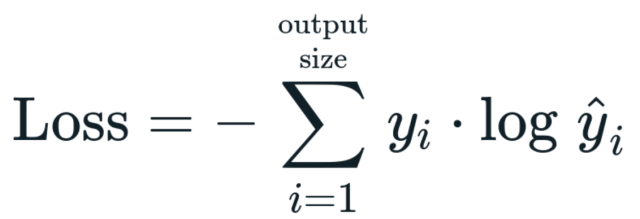
Leave a Reply