In this post, you will be introduced to some of the important class of algorithms and related computational tasks which could be taken care using these algorithms.
Here are some important classes of algorithms which will be briefly discussed in this post:
- Divide and conquer algorithms
- Graphs based algorithms
- Greedy algorithms
- Dynamic programming
- Linear programming
- NP-complete algorithms
- Quantum algorithms
Divide-and-Conquer Algorithms
Divide and conquer algorithms are the algorithms which can be used to solve problems using divide and conquer strategy. The following represents the steps of divide-and-conquer algorithms:
- Breaking it into subproblems that are themselves smaller instances of the same type of problem
- Recursively solving these subproblems
- Appropriately combining their answers
The following represents some of the examples of divide and conquer algorithms:
- Search algorithms such as binary search
- Sorting algorithms such as mergesort
Further details could be read from this page – Divide and conquer algorithms
Graph-based Algorithms
A wide-range of problems can be expressed in form of graphs with vertices (also called as nodes) and edges between these nodes. These problems can be solved using what can be called as graph-based algorithms. Internet or WWW consisting of billions of websites could be represented as a graph. Each of the website can be represented as a vertices and the links between one website to another can be represented as edges.
Graph can be categorized into two different kinds – A. Directed Acyclic Graph (DAG) B. Undirected Graph. The following picture represents different kind of graphs. Real-world problems can be modelled into one of these kinds and graph-based algorithms can be applied appropriately to solve the problem.
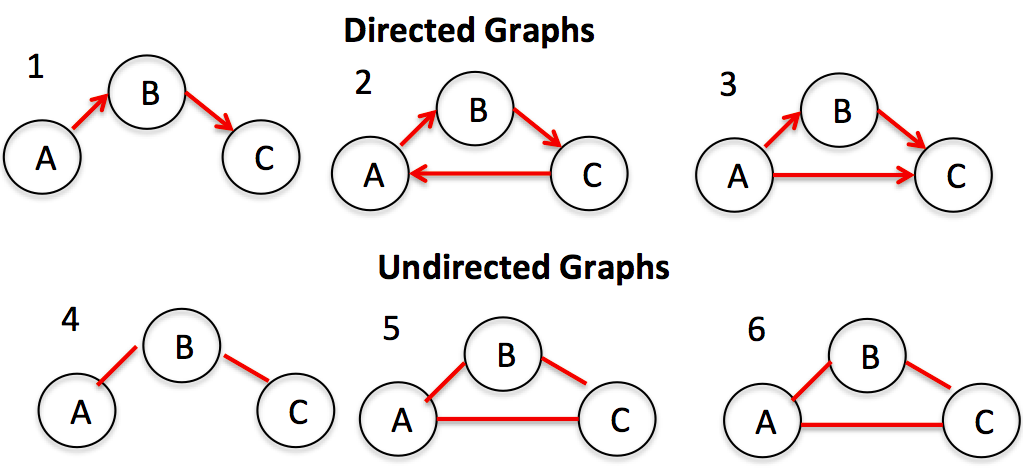
A graph can be represented as adjacency matrix or adjacency list. I will deal with further details on how to model a real-world problem on one of these types. Check out further details on this page – Decomposition of graphs, Paths in graphs
Greedy Algorithms
There are various different real-world problems where the immediate benefit is more important than the future benefits. These are the problems where greedy algorithms would prove to be most appropriate. Greedy algorithms build up a solution piece by piece, always choosing the next
piece that offers the most obvious and immediate benefit. One such example of greedy algorithm is minimum spanning trees.
Further details on greedy algorithms can be found on this page – Greedy Algorithms.
Dynamic Programming
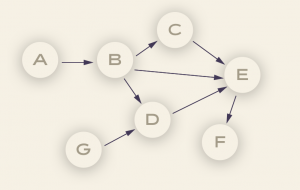
Dynamic programming is an algorithmic paradigm in which a problem is solved by identifying a collection of subproblems and tackling them one by one. The solution to smaller problems are found and used to solve the larger ones until the whole problem is solved. The approach to dynamic programming is based on the DAG (Directed Acyclic Graphs). The nodes of DAG can be thought of as the subproblems and its edges can be thought of as dependencies between the subproblems. Let’s understand this with the following DAG:
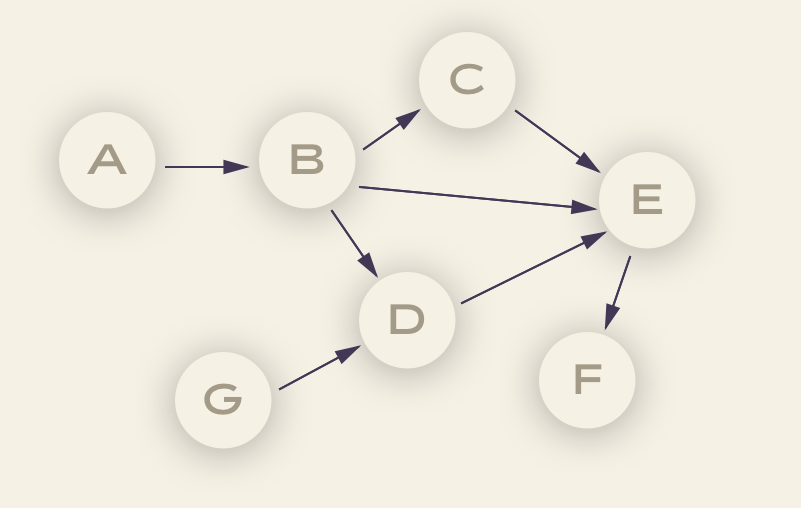
Let’s say a problem is defined using DAG where the nodes represent the sub-problems. In order to solve the subproblem C, there is a need to solve the problem represented using B. Thus, the solution to subproblem C requires the solution to subproblem B to be found. Thus, this dependency is represented using edge between B and C. In the above DAG, the subproblem represented using node B can be thought of as smaller problem. Similarly, the subproblem represented using A is smaller than B.
Solving subproblems in consecutive nodes will result in having the main problem solved. Here, node F can be seen as the whole problem. Read further details from this page – Dynamic programming.
Linear Programming
Linear programming represents algorithms which could broadly be represented as optimization tasks. These optimisation tasks require one or more constraints to be fulfilled / satisfied. There could be one or more solutions to the optimization tasks where the constraints can be satisfied. However, the solution which satisfies some well-defined optimisation criteria is the one which gets selected as the final solution. Both the constraints and the optimization criteria can be represented as the linear functions (hence, linear programming).
The problems which can be expressed as the optimization problems are the ones which could be solved based on the principles of linear programming. The linear programming problems can be expressed in form of the following:
- One or more set of variables whose values need to be determined
- A linear objective function (having these variables) which needs to be optimized (minimised or maximised)
- Values of these variables need to satisfy one or more constraint functions (linear functions)
The following are some real-world examples where linear programming can be applied:
- Profit maximisation: Given that a firm produces X1 units of product A and X2 units of product B, how much should the value of X1 and X2 be, in order to maximise the profit made by selling the products A and B.
- Production planning: In a manufacturing plant, often, there is a need to do production planning in relation to manufacturing Xi number of product units while involving some Yi number of employees every month. There can be other variables which will need to be determined, for example – number of units to be stored every month etc. This problem can be solved using linear programming.
Further reading can be done on this page – Linear Programming
Quantum Algorithms
Quantum algorithms are the algorithms which need quantum computing for execution. Quantum computing is based on the Quantum Physics principles. The key concepts or features of Quantum Physics are Qubits, superposition principle and measurement of quantum state. The details could be read and understood from this page – Quantum Algorithms.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com
- MSE vs RMSE vs MAE vs MAPE vs R-Squared: When to Use? - April 22, 2024
- Gradient Descent in Machine Learning: Python Examples - April 22, 2024
- Loss Function vs Cost Function vs Objective Function: Examples - April 19, 2024
Leave a Reply