What is information theory? How is information theory related to machine learning? These are some of the questions that we will answer in this blog post. Information theory is the study of how much information is present in the signals or data we receive from our environment. AI / Machine learning (ML) is about extracting interesting representations/information from data which are then used for building the models. Thus, information theory fundamentals are key to processing information while building machine learning models. In this blog post, we will provide examples of information theory concepts and entropy concepts so that you can better understand them. We will also discuss how concepts of information theory, entropy, etc are related to machine learning.
What is information theory and what are its key concepts?
Information theory is the study of encoding, decoding, transmitting, and manipulating information. Information theory provides tools & techniques to compare and measure the information present in a signal. In simpler words, how much information is present in one or more statements is a field of study called information theory.
The greater the degree of surprise in the statements, the greater the information contained in the statements. For example, let’s say commuting from place A to B takes 3 hours on average and is known to everyone. If somebody makes this statement, the statement provides no information at all as this is already known to everyone. Now, if someone says that it takes 2 hours to go from place A to B provided a specific route is taken, then this statement consists of good bits of information as there is an element of surprise in the statement.
The extent of information required to describe an event depends upon the possibility of occurrence of that event. If the event is a common event, not much information is required to describe the event. However, for unusual events, a good amount of information will be needed to describe such events. Unusual events have a higher degree of surprises and hence greater associated information.
The amount of information associated with event outcomes depends upon the probability distribution associated with that event. In other words, the amount of information is related to the probability distribution of event outcomes. Recall that the event and its outcomes can be represented as the different values of the random variable, X from the given sample space. And, the random variable has an associated probability distribution with a probability associated with each outcome including the common outcomes consisting of less information and rare outcomes consisting of a lot of information. The higher the probability of an event outcome, the lesser the information contained if that outcome happens. The smaller the probability of an event outcome, the greater the information contained if that outcome with lesser probability happens.
How do we measure the information?
There are the following requirements for measuring the information associated with events:
- Information (or degree of surprise) associated with a single discrete event: The information associated with a single discrete event can be measured in terms of the number of bits. Shannon introduced the term bits as the unit of information. This information is also called self-information.
- Information (or degree of surprise) associated with the random variable whose values represent different event outcomes where the values can be discrete or continuous. Information associated with the random variable is related to probability distribution as described in the previous section. The amount of information associated with the random variable is measured using Entropy (or Shannon Entropy).
- The entropy of the event representing the random variable equals the average self-information from observing each outcome of the event.
What is Entropy?
Entropy represents the amount of information associated with the random variable as the function of the probability distribution for that random variable, be the probability distribution be probability density function (PDF) or probability mass function (PMF). The following is the formula for the entropy for a discrete random variable.
Where Pi represents the probability of a specific value of the random variable X. The following represents the entropy of a continuous random variable. It is also termed differential entropy.
How are information theory, entropy, and machine learning related?
Machine learning (ML) models are about building models using the representation of data in the way that the representations consist of a lot of information. The representation is also termed features. These representations are crafted manually by data scientists or using deep learning algorithms such as autoencoders. However, the goal is to come up with representations that consist the most of the information useful for building models that generalize well by making accurate predictions on the unseen data.
Information theory is the study of extracting information from the data or signals related to an event. The information represents the degree of surprise associated with the data, signal, or statements. The greater the degree of surprise, the greater the information. The key concept in information theory is entropy which represents the amount of information present in the data or signals. The entropy is associated with the probability distribution related to the outcomes of the event (random variable). The higher the probability of occurrence of an event, the lesser the information from that outcome.
The performance of the machine learning models depends upon how close is the estimated probability distribution of the random variable (representing the response variable of ML models) against their true probability distribution. This can be measured in terms of the entropy loss between the true probability distribution and the estimated probability distribution of the response variable. This is also termed cross-entropy loss as it represents entropy loss between two probability distributions. Recall that entropy can be calculated as a function of probability distribution related to different outcomes of the random variables.
The goal of training a classification machine learning model is to come up with a model which predicts the probability of the response variable belonging to different classes, as close to true probability. If the model predicts the class as 0 when the true class is 1, the entropy is very high. If the model predicts the class as 0 when the true class is 0, the entropy is very low. The goal is to minimize the difference between the estimated probability and true probability that a particular data set belongs to a specific class. In other words, the goal is to minimize the cross-entropy loss – the difference between the true and estimated probability distribution of the response variable (random variable).
The goal is to maximize the occurrence of the data set including the predictor dataset and response data/label. In other words, the goal is to estimate the parameters of the models that maximize the occurrence of the data set. The occurrence of the dataset can be represented in terms of probability. Thus, maximizing the occurrence of the data set can be represented as maximizing the probability of occurrence of the data set including class labels and predictor dataset. The following represents the probability that needs to be maximized based on the estimation of parameters. This is also called maximum likelihood estimation. The probability of occurrence of data can be represented as the joint probability of occurrence of each class label. Assuming that every outcome of the event is independent of others, the probability of occurrence of the data can be represented as the following: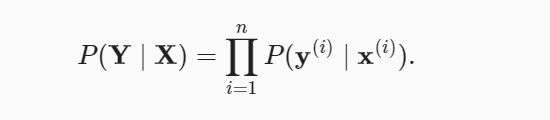 
According to the maximum likelihood estimation, maximizing the above equation is equivalent to minimizing the negative log-likelihood of the following:
In the case of softmax regression, for any pair of true label vs predicted label for Q classes, the loss function can be calculated as the following:
While training machine learning models for the classification problems, the goal remains to minimize the loss function across all pairs of true and predicted labels. The goal is to minimize the cross-entropy loss.
Conclusion
Information theory, entropy, and machine learning are all related to each other. Information theory deals with extracting information from data or signals. Entropy is a measure of the information contained in the data or signal. Machine learning models are designed to minimize the loss of information or entropy between the estimated and true probability distributions. This is also termed cross-entropy loss. When training classification models, the goal is to minimize the information loss between estimated and true probability distribution.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
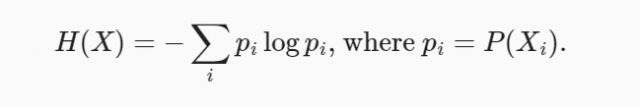
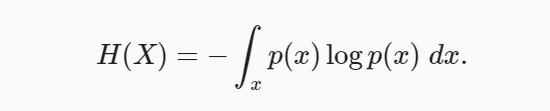
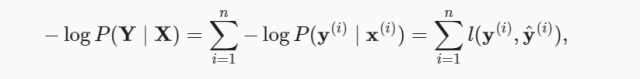
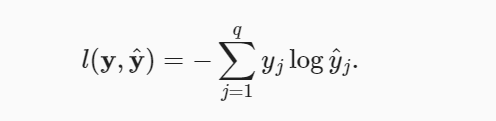
I found it very helpful. However the differences are not too understandable for me