In this post, you will learn about one of the popular and powerful ensemble classifier called as Voting Classifier using Python Sklearn example. Voting classifier comes with multiple voting options such as hard and soft voting options. Hard vs Soft Voting classifier is illustrated with code examples. The following topic has been covered in this post:
- Voting classifier – Hard vs Soft voting options
- Voting classifier Python example
Voting Classifier – Hard vs Soft Voting Options
Voting Classifier is an estimator that combines models representing different classification algorithms associated with individual weights for confidence. The Voting classifier estimator built by combining different classification models turns out to be stronger meta-classifier that balances out the individual classifiers’ weaknesses on a particular dataset. Voting classifier takes majority voting based on weights applied to the class or class probabilities and assigns a class label to a record based on majority vote. The ensemble classifier prediction can be mathematically represented as the following:
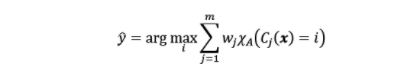
In above equation, [latex]C_j[/latex] represents the classifer, [latex]w_j[/latex] represents the weight associated with the prediction of the classifier. There are two different types of voting classifier. They are as following:
- Hard voting classifier
- Soft voting classifier
Hard Voting Classifiers – How do they work?
Hard voting classifier classifies input data based on the mode of all the predictions made by different classifiers. The majority voting is considered differently when weights associated with the different classifiers are equal or otherwise.
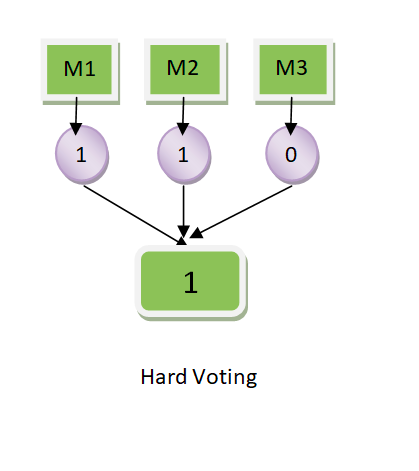
Majority Voting based on equal weights: When majority voting is taken based equal weights, mode of the predicted label is taken. Let’s say there are 3 classifiers, clf1, clf2, clf3. For a particular data, the prediction is [1, 1, 0]. In case, the weights assigned to the classifiers are equal, the mode of the prediction is taken. Thus, the mode of [1, 1, 0] is 1 and hence the predicted class to the particular record becomes class 1. For equal weights, the equation in fig 1 gets simplified to the following:
mode [latex]clf_1, clf_2, clf_3[/latex]
mode[1, 1, 0] = 1
Diagrammatically, this is how the hard voting classifier with equal weights will look like:
Majority voting based on different weights: When majority vote is taken based on different weights, the final prediction is computed appropriately. Let’s say there are 3 classifiers, clf1, clf2, clf3 and the predictions from these classifiers have weights defined as [0.1, 0.3, 0.6]. For a particular data, if the prediction is [0, 0, 1] by classifiers clf1, clf2 and clf3. Applying the weights [0.1, 0.3, 0.6] to the prediction [0, 0, 1], the equation in fig 1 simplies and results into the prediction as class 1 as shown below:
mode [0, 0, 0, 0, 1, 1, 1, 1, 1, 1] = 1
Soft Voting Classifiers – How do they work?
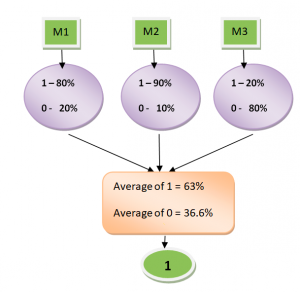
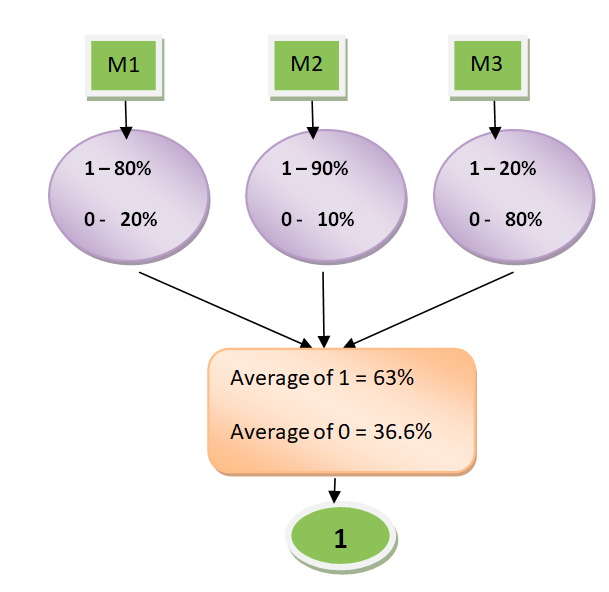
Soft voting classifier classifies input data based on the probabilities of all the predictions made by different classifiers. Weights applied to each classifier get applied appropriately based on the equation given in Fig 1. Lets understand this using an example. Let’s say there are two binary classifiers clf1, clf2 and clf3. For a particular record, the classifiers make the following predictions in terms of probabilities in favour of classes [0,1]:
clf1 -> [0.2, 0.8], clf2 -> [0.1, 0.9], clf3 -> [0.8, 0.2]
With equal weights, the probabilities will get calculated as the following:
Prob of Class 0 = 0.33*0.2 + 0.33*0.1 + 0.33*0.8 = 0.363
Prob of Class 1 = 0.33*0.8 + 0.33*0.9 + 0.33*0.2 = 0.627
The probability predicted by ensemble classifier will be [36.3%, 62.7%]. The class will most likely by class 1 if the threshold is 0.5. This is how a soft voting classifier with equal weights will look like:
With unequal weights [0.6, 0.4], the probabilities will get calculated as the following:
Prob of Class 0 = 0.6*0.2 + 0.4*0.6 = 0.36
Prob of Class 1 = 0.6*0.8 + 0.4*0.4 = 0.64
The probability predicted by ensemble classifier will be [0.36, 0.64]. The class will most likely by class 1 if the threshold is 0.5.
Voting Classifier Python Example
In this section, you will see the Python example in which Sklearn.ensemble VotingClassifier is used. Pay attention to some of the following in the code:
- Two probabilistic classifiers trained using LogisticRegression and RandomForestClassifier is trained on Sklearn breast cancer dataset.
- RandomizedSearchCV is used for tuning both the LogisticRegression and RandomForestClassifier model
- Pipeline is used to create estimators for both the algorithms.
- Both hard and soft VotingClassifier is used for illustration purpose.
Here are the code illustrating how the estimator is fit with training dataset using Logistic Regression:
#
# Creating param_distributions
#
param_distributions_lr = [{
'logisticregression__C': stats.expon(scale=100)
}]
#
# Creating a pipeline with LogisticRegression
#
pipeline_lr = make_pipeline(StandardScaler(),
LogisticRegression(solver='lbfgs',
penalty='l2',
max_iter = 10000,
random_state=1))
#
# Creating a randomized search for getting best estimator
#
rsLR = RandomizedSearchCV(pipeline_lr, param_distributions=param_distributions_lr,
scoring='accuracy',
cv = 10, refit=True,
random_state=1)
#
# Fit the model
#
rsLR.fit(X_train, y_train)
Here are the code illustrating how the estimator is fit with training dataset using RandomForestClassifier:
#
# Creating param_distributions
#
param_distributions_rfc = [{
'randomforestclassifier__n_estimators': [int(x) for x in np.linspace(10, 200, num = 50)],
'randomforestclassifier__max_depth': [int(x) for x in np.linspace(2, 10, num = 5)],
'randomforestclassifier__max_features': ['auto', 'sqrt'],
}]
#
# Creating a pipeline with LogisticRegression
#
pipeline_rfc = make_pipeline(StandardScaler(),
RandomForestClassifier(random_state=1))
#
# Creating a randomized search for getting best estimator
#
rsRFC = RandomizedSearchCV(pipeline_rfc, param_distributions=param_distributions_rfc,
scoring='accuracy',
cv = 10, refit=True,
random_state=1)
#
# Fit the model
#
rsRFC.fit(X_train, y_train)
Once both the estimators based on LogisticRegression and RandomForestClassifier is fit, the best estimators using two different classifiers are derived using the following code. These classifiers will be used for creating the voting classifier.
clfLR = rsLR.best_estimator_
clfRFC = rsRFC.best_estimator_
Now, its time to create both the hard and soft voting classifier. Note how the weights are assigned to [2, 1] and voting options assigned to hard and soft.
#
# Voting Classifier with voting options as hard
#
ensemble_clf_hard = VotingClassifier(estimators=[
('lr', clfLR), ('rfc', clfRFC)], voting='hard', weights=[2, 1])
#
# Fit the model with voting classifier
#
ensemble_clf_hard.fit(X_train, y_train)
#
# Voting Classifier with voting options as soft
#
ensemble_clf_soft = VotingClassifier(estimators=[
('lr', clfLR), ('rfc', clfRFC)], voting='soft', weights=[2, 1])
#
# Fit the model with voting classifier
#
ensemble_clf_soft.fit(X_train, y_train)
This is how the output of fitting the hard voting classifier would look like:
Conclusions
In this post, you learned some of the following in relation to using voting classifier with hard and soft voting options:
- Voting classifier can be seen as a stronger meta-classifier that balances out the individual classifiers’ weaknesses on a particular dataset.
- Voting classifier is an ensemble classifier which takes input as two or more estimators and classify the data based on majority voting.
- Hard voting classifier classifies data based on class labels and the weights associated with each classifier
- Soft voting classifier classifies data based on the probabilities and the weights associated with each classifier
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
Hello sir, would you please help me out to understand how the weight was adjusted as 2, 1 during hard voting? Sorry, if I missed the concept.