There are many different ways in which machine learning (ML) models’ fairness could be determined. Some of them are statistical parity, the relative significance of features, model sensitivity etc. In this post, you would learn about how model sensitivity could be used to determine model fairness or bias of model towards the privileged or unprivileged group. The following are some of the topics covered in this post:
- How could Model Sensitivity be used to determine Model Bias or Fairness?
- Example – Model Sensitivity & Bias Detection
How could Model Sensitivity determine Model Bias or Fairness?
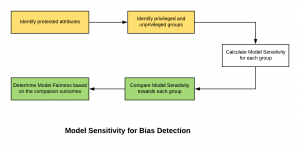
Model sensitivity could be used as a fairness metrics to measure the model bias towards the privileged or unprivileged group. Higher the sensitivity of model for the unprivileged group than the privileged group, greater is the benefit the model looks to provide to the privileged group. Alternatively, lower the sensitivity of model for the unprivileged group than the privileged group, greater is the benefit the model provides to the unprivileged group. The diagram given below represents the steps which could be taken to use model sensitivity for determining the model fairness:
Let’s try and understand with examples. Recall that Sensitivity is defined as the percentage of true positives or the rate of true positives. In simpler words, Sensitivity is the measure of the extent to which the model is correct in making true predictions about the positive cases. Mathematically, it can be represented as the following:
Sensitivity = True Positive Predictions / Actual Positive Cases
The above could also be represented as a function of predictions as shown in the following. Actual positive cases could be represented as a function of true positive and false negative (Positives which got incorrectly predicted as negative)
Sensitivity = True Positive Predictions / (True Positive Predictions + False Negative Predictions)
Going by the above, high value of sensitivity (very near to but less than 1) would mean that the value of true positive predictions (numerator) is very near (but less) than the denominator (true positives + false negatives). This implies that the value of false negative predictions would be very small. This would further mean that only a few instances of actual positive cases got predicted incorrectly as negative. The model was very accurate in predicting positive cases. Going by the similar logic, lower sensitivity value would mean that the model was not very accurate in predicting positive cases. There were many instances of positives which got predicted as negatives (and, hence false negative).
Lower sensitivity for the privileged group would mean that the model looks to be favoring the privileged group by not predicting many positive cases as the positive. In other words, the model looks to be favoring privileged group by predicting several positive cases as negatives. Thus, the model could be said to be unfair. Lower the model sensitivity value of a particular group, greater biased the model is toward that group, and thus, greater unfair the model is against another group found with the comparatively higher value of model sensitivity. Thus, it could be seen that the value of model sensitivity could be used to comprehend the model fairness towards the privileged or unprivileged group.
The model would be said to be fair if the value of model sensitivity for the privileged and unprivileged group are very close to each other if not same.
Example – Model Sensitivity & Bias Detection
Let’s take an example to understand how could the model bias be evaluated as a function of model sensitivity using a model that predicts whether a person would re-offend. Instinctively (based on implicit human bias), it is one of the specific “gender” (male or female) against which the model could get biased as like in the real world in predicting whether those with a specific gender could re-offend or not. Thus, one of the protected attributes becomes gender. For the current example, in the real world, one could get biased in favor of female and not (or fail to) classify them as the ones who could re-offend. Thus, those having female gender could be called out as the privileged group which could be said to be placed at a systematic advantage by the model. Alternatively, the male ones could be called out as the unprivileged group which could be said to be placed at a systematic disadvantage.
The goal is to measure whether the model provides benefits to the privileged group or unprivileged group and hence biased towards the privileged or unprivileged group. This would be measured as a function of the difference between the sensitivity of unprivileged and privileged groups.
One of the techniques of determining whether the model is biased towards (in favor of) the privileged group is by calculating the sensitivity of the model towards the privileged group (females in the current example). A high value of sensitivity for females would mean that the model has mostly predicted correctly about the positive cases in case of the female. This means that most of the female who reoffended were found to be predicted correctly. And, there is only very less number of the female who got favor in terms of getting classified as good (negative) although they were re-offender (positive) which essentially means that the value of the false negatives is very less. Thus, the model does not provide any benefits to the females. And, hence, the model does not look to be biased toward female as most of the female offenders got predicted correctly. On the other hand, a low value of sensitivity would mean that there was a very large number of females who got favored in terms of getting classified as good (negative) although they were found to be re-offenders (positive). This resulted in female getting benefitted as a result of the model prediction. And, hence, the model could be said to be biased in favor of the female. The same analogy could be applied to male as well.
It could be seen that the group having a lower model sensitivity (than other) could be said to be benefitted more by the model. In other words, the model could be said to be biased (hence, unfair) against the group having comparatively higher sensitivity value.
References
- IBM AI Bias Toolkit – Equal Opportunity Difference
- ML Model Sensitivity & Specificity
- Sensitivity vs Specificity – Difference
Summary
In this post, you learned about how model sensitivity could be used for determining model fairness. A model would be said to be fair (unbiased) if it is equally sensitive (true positive rates) to both privileged and unprivileged groups. A model which is lesser sensitive (high number of false negatives) to one of the groups could be seen as providing benefit to that group as a large number of instances would be classified as negative although they ain’t (and, hence, false negative).
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com
- MSE vs RMSE vs MAE vs MAPE vs R-Squared: When to Use? - April 22, 2024
- Gradient Descent in Machine Learning: Python Examples - April 22, 2024
- Loss Function vs Cost Function vs Objective Function: Examples - April 19, 2024
Leave a Reply