Prescriptive analytics plays a significant role in helping organizations make informed decisions by recommending the best course of action given a specific situation. Unlike descriptive and predictive analytics, which focus on understanding past data and predicting future outcomes, prescriptive analytics aims to optimize decision-making processes. Optimization solutions are a key component of prescriptive analytics, enabling decision-makers to find the most efficient and effective strategies to achieve their goals.
Convex Optimization is a special class of optimization problems that deals with minimizing (or maximizing) convex functions over convex sets. Convex functions and sets exhibit specific mathematical properties that make them particularly well-suited for optimization. In the context of prescriptive analytics, convex optimization plays a key role in solving various optimization problems, such as resource allocation, scheduling, portfolio optimization, etc. It has much broader applicability beyond mathematics to disciplines like Machine learning, data science, economics, medicine, and engineering. By leveraging the unique properties of convex optimization, data scientists can develop efficient algorithms to find optimal solutions to real-world challenges and create robust prescriptive analytics solutions. In this blog post, you will learn about convex optimization concepts and different techniques with the help of examples.
What is Convex Optimization?
Convex optimization is a powerful tool used to solve optimization problems in various fields such as finance, engineering, and machine learning. In a convex optimization problem, the goal is to find a point that maximizes or minimizes the objective function. This is achieved through iterative computations involving convex functions, which are functions that always lie above their chords.
The objective function is subject to both equality and inequality constraints. An equality constraint requires the solution to be exactly at a given point, while an inequality constraint restricts the solution to a certain range. These constraints are critical in defining the feasible region, which is the set of all solutions that satisfy the constraints.
Convex optimization can be used to optimize algorithms by improving the speed at which they converge to a solution. Additionally, it can be used to solve linear systems of equations by finding the best approximation to the system, rather than computing an exact answer.
Convex optimization plays a critical role in training machine learning models, which involves finding the optimal parameters that minimize a given loss function. In machine learning, convex optimization is used to solve a wide range of problems such as linear regression, logistic regression, support vector machines, and neural networks. The following are some applications of convex optimization in training machine learning models:
- Training linear regression models is a classic example of a convex optimization problem in which the goal is to find the best-fit line that minimizes the sum of squared errors between the predicted and actual values. The optimization problem can be formulated as a convex quadratic programming problem, which can be solved efficiently using convex optimization techniques.
- Training logistic regression models is another example of machine learning technique that involves finding the optimal parameters that maximize the likelihood of the observed data. This optimization problem can be formulated as a convex optimization problem with a log-concave objective function. The use of convex optimization techniques ensures that the optimization problem has a unique global minimum, making it more efficient to find the optimal solution.
Convexity plays an important role in convex optimizations. Convexity is defined as the continuity of a convex function’s first derivative. It ensures that convex optimization problems are smooth and have well-defined derivatives to enable the use of gradient descent. Some examples of convex functions are linear, quadratic, absolute value, logistic, exponential functions among others.
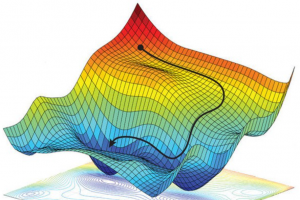
For convexity, convex sets are the most important. A convex set is a set that contains all points on or inside its boundary and contains all convex combinations of points in its interior. A convex set is defined as a set of all convex functions. Simply speaking, the convex function has a shape that is like a hill. A convex optimization problem is thus to find the global maximum or minimum of convex function. Convex sets are often used in convex optimization techniques because convex sets can be manipulated through certain types of operations to maximize or minimize a convex function. An example of a convex set is a convex hull, which is the smallest convex set that can contain a given convex set. A convex function takes the value only between its minimum and maximum values on any convex interval. This means that there exist no local extremes for this convex function (on the convex region). It also conveys that among all the points of this set which are on the convex hull, only one point is closest to the minimum.
Convex optimization problems can be broadly classified into the following two types:
- Constrained convex optimization: Constrained convex optimization involves finding the optimal solution to a convex function subject to convex constraints. These constraints may include both equality and inequality constraints. The objective function may be subject to a constraint that requires it to lie exactly at a given point or within a specified range. An example of a constrained convex optimization problem is portfolio optimization, where the goal is to find the optimal allocation of investments subject to constraints on risk and return.
- Unconstrained convex optimization: Unconstrained convex optimization involves finding the optimal solution to a convex function without any constraints. In this case, the objective function is simply a convex function that needs to be minimized or maximized. An example of an unconstrained convex optimization problem is linear regression, where the goal is to find the best-fit line that minimizes the sum of squared errors between the predicted and actual values.
What are different techniques that are used for convex optimization?
There are a variety of approaches for performing convex optimization. Some of them are following:
- Gradient methods using derivatives: One of the approaches to convex optimization is via first computing the convex function’s gradient, then using this derivative for performing convex optimization. If the convex problem has an easily computable convex objective function, then this gradient method of convex minimization can be used. This is because you are using information about the convex function to construct each step in the optimization. This convex optimization technique is widely used for solving convex problems.
- Projected gradient methods: This convex optimization approach was first introduced for solving convex problems with convex objective functions and convex constraints. It has an advantage over gradient methods using derivatives, if the system of convex constraints is not satisfied at the current iterate, it simply projects onto the subspace defined by these convex constraints.
- Quasi-Newton methods: This convex optimization approach is based on approximating the Hessian matrix of second derivatives by a quadratic approximation (where any convex function such as a linear one, can be used). The convex problem with convex constraints is solved using the quasi-Newton method to converge faster. It employs both first and second derivatives of convex objective functions to iteratively compute convex function minima using only function evaluations. The algorithm uses quadratic approximations around convex minimization iterations, thus requiring only function evaluations. An initial point is required to start convex optimization.
- Interior point methods using convex conjugate gradients and barrier function: If convexity is easy to check and convex function is twice differentiable, then the barrier function convex conjugate gradient method can be used to solve convex optimization problems. The two methods combined also make it easier to avoid going into a local minimum- there’s a gradient test before each iteration that checks if the step would go towards a local minimum.
- Global convex minimization: For convex problems, the quasi-Newton method usually gives better convergence results when compared with other techniques such as the gradient-based methods and the barrier function convex conjugate gradient method. However this might not always be the case, there might be convex problems where the quasi-Newton method converges slowly or even in a non-convergent manner. In such cases, an alternative approach is to use a global convex minimization technique instead of a local convex minimization technique.
- The method of multipliers: This convex optimization approach consists of iterations that change the original convex constraints into equality constraints by multiplying each constraint with a fixed multiplier so that the convex problem has convex objective functions and convex equality constraints at its minimization iterations.
- Modified optimization methods: The convex optimization problem can also be solved by modifications of Newton’s method. This convex optimization approach is suitable for convex functions which are only slightly convex, but not strongly convex. This convex optimization approach can be used to solve convex problems where the first or second derivative of convex objective functions cannot be computed easily.
- Reduced rank convex optimization: Convex functions can also be minimized by solving a reduced rank convex minimization problem. This is done by computing a convex function of a convex function. This convex optimization approach is suitable for convex functions with a bounded gradient, which means that the function has only finitely many critical points.
- Sequential convex programming: Sequential convex programming (SCP) is used for convex optimization problems that are convex but not strongly convex. It forms an iterative sequence that gradually improves the objective value, stopping when a user-specified termination criterion is satisfied or when no improvement to the objective function value is made within a user-specified number of iterations. The convex optimization problem is convex, even though it contains non-convex components.
- Likelihood ratio methods: For convex minimization problems, where convexity of the objective function is easy to check or convex constraints are convex but not strongly convex, likelihood ratio methods can be used to solve them. This convex optimization approach is suitable for convex functions which have a bounded gradient, convex constraints, and convex objective function with a single global minimizer.
- Stochastic optimization methods: In some cases, the convex optimization problem might not have an easily computable convex function with a Lipschitz continuous gradient. In those cases, gradients will not be used for convex optimization. Because of this, convex optimization problems can also be solved by simulation methods.
- Evolutionary algorithms: Evolutionary algorithms are not convex but they can still solve convex problems if the convex function has a bounded gradient or convex constraints with convex components or finite optimum points. This is done by perturbing the convex function components, which makes these convex optimization problems convex.
Real-world example of convex optimizations
Some real-life examples of convex optimization problems include the following:
- Scheduling of flights: Flight scheduling is an example convex optimization problem. It involves finding flight times that minimize costs like fuel, pilot/crew costs, etc. while maximizing the number of passengers.
- Facility location: Facility location problems are constructed to optimize the use of resources within a facility. These types of problems appear in many different fields such as logistics, telecommunications, and manufacturing.
- Inventory management: In inventory management, the optimization problem is to minimize the overall costs of ordering, holding, and shortage while maintaining stocks within the desired point.
- Routing phone calls: Convex programming has been applied to the general network design problem for routing telephone calls, which is an example convex optimization problem. The challenge with routing phone calls is finding the shortest path that connects a set of phone callers with a set of receivers.
- Fleet management: Convex optimization can be used to minimize the total operating costs of a fleet, subject to certain travel and scheduling restrictions.
- Logistics: Convex optimization problems in logistics deal with finding the number and type of vehicles that should be used for conveying goods from a set of agents (e.g. warehouses) to a set of customers (e.g. retail stores).
- Optimizing wind turbine output: Convex optimization has been applied to the control of wind turbines, where wind speed is modeled as a convex function of the turbine control variables.
- Energy consumption: Optimization of energy consumption in buildings is an example convex optimization problem that has been studied by many researchers. The convex objective function models the total cost to operate the building, which includes heating, cooling, lighting and other operational costs. Convex constraints are used to model restrictions on the control variables, such as occupancy sensors and timers.
- eCommerce: In eCommerce, convex optimization is used to minimize the cost of fulfilling orders. For example, minimizing the cost to fulfill an order while meeting demand constraints. It is also used in revenue management to maximize expected profit for a period of time given capacity and demand constraints.
- Campaign management: In marketing campaign management, convex optimization is used to determine the optimal locations and levels of customer service given fixed costs. It can also be used to find the optimal distribution channels for conveying information about products to customers, given fixed costs and expectations on consumer response.
In convex optimization, the function to be minimized or maximized is convex. A convex problem has an inequality constraint in which all variables are greater than or equal to zero (or alternatively less than or equal to zero). The gradient of this type of convex function will always point uphill, so it can’t get stuck at a local minimum that isn’t global. It’s also impossible for two gradients on opposite sides of the graph slope up and down in parallel because they’re not differentiable at their intersection point. This means that there is no need for iterations when using convex optimization techniques like machine learning algorithms – instead they work by simply moving downhill until reaching the optimum value. Convex problems can be solved on a convex minimization or convex maximization problem. Most machine learning algorithms like gradient descent, coordinate descent and batch gradient descent are used for convex optimization problems.
- Mathematics Topics for Machine Learning Beginners - July 6, 2025
- Questions to Ask When Thinking Like a Product Leader - July 3, 2025
- Three Approaches to Creating AI Agents: Code Examples - June 27, 2025
sir,
Your article is very informative.
Which optimization technique is best for frequent pattern mining of temporal data.
Kindly suggest some techniques, as I am a Ph.D. scholar.