Last updated: 5th Jan, 2024
Cohen’s Kappa Score is a statistic used to measure the performance of machine learning classification models. In this blog post, we will discuss what Cohen’s Kappa Score is and Python code example representing how to calculate Kappa score using Python. We will also provide a code example so that you can see how it works!
What is Cohen’s Kappa Score or Coefficient?
Cohen’s Kappa Score, also known as the Kappa Coefficient, is a statistical measure of inter-rater agreement for categorical data. Cohen’s Kappa Coefficient is named after statistician Jacob Cohen, who developed the metric in 1960. It is generally used in situations where there are two raters, but it can also be adapted for use with more than two raters. For machine learning binary classification models, one of the raters become the classification model and the other rater becomes the real-world observer who knows the actual truth about the categories of each of the record or dataset.
Cohen’s Kappa takes into account both the number of agreements (True positives & true negatives) and the number of disagreements between the raters (False positives & false negatives), and it can be used to calculate both overall agreement and agreement after chance has been taken into account. Taking that into consideration, Cohen’s Kappa score can be defined as the metric used to measure the performance of machine learning classification models based on assessing the perfect agreement and agreement by chance between the two raters (real-world observer and the classification model).
The main use of Cohen Kappa metric is to evaluate the consistency of the classifications, rather than their accuracy. This is particularly useful in scenarios where accuracy is not the only important factor, such as with imbalanced classes.
Cohen’s Kappa Score Value Range (-1 to 1)
The Cohen Kappa Score is used to compare the predicted labels from a model with the actual labels in the data. The score ranges from -1 (worst possible performance) to 1 (best possible performance).
- A Kappa value of 1 implies perfect agreement between the raters or predictions.
- A Kappa value of 0 implies no agreement other than what would be expected by chance. In other words, the model is no better than the random guessing.
- Negative values indicate agreement less than chance (which is a rare but concerning scenario).
The following is the white paper on Cohen Kappa Score: J. Cohen (1960). “A coefficient of agreement for nominal scales”. Educational and Psychological Measurement
How to Calculate Cohen’s Kappa Score?
Cohen’s Kappa can be calculated using either raw data or confusion matrix values. When Cohen’s Kappa is calculated using raw data, each row in the data represents a single observation, and each column represents a rater’s classification of that observation. Cohen’s Kappa can also be calculated using a confusion matrix, which contains the counts of true positives, false positives, true negatives, and false negatives for each class. We will look into the details of how Kappa score can be calculated using confusion matrix.
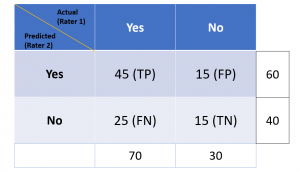
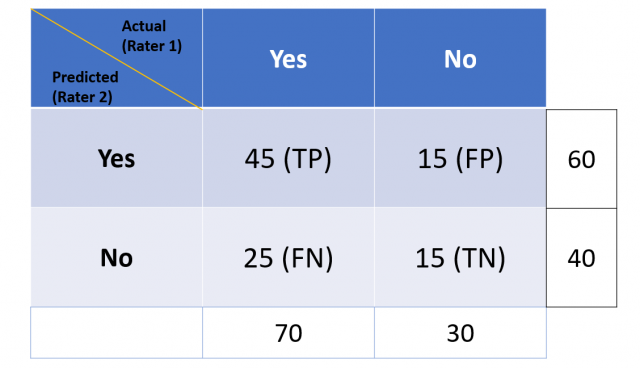
Let’s look at the following confusion matrix representing a binary classification model where there are two classes / labels:
Lets quickly understand the concepts of true positives, false positives, true negative, false negatives:
- True Positives (TP) – These are the correctly predicted positive values. In this case, both the raters (observer in real-world and classification model) are in agreement.
- False Positives (FP) – These are the incorrectly predicted positive values. In other words, these are instances which are predicted as positive although they are truly negative. Observer and classification are in disagreement about the true negatives. These are instances which are called out negative by the observer but the positive (falsely) by the classification model.
- True Negatives (TN) – These are the correctly predicted negative values. The observer and the classification are in perfect agreement about the negatives.
- False Negatives (FN) – These are incorrectly predicted negative values. The observer and the classification models are in disagreement about the true positives. These are instances which are called out positive by the observer but the negative (falsely) by the classification model.
In the above confusion matrix, the actual represents rater 1. Rater 1 is an observer of real world events and record what actually happened. The predicted represents rater 2. The rater 2 represents the classification model which makes the predictions. Cohen Kappa score will be used to assess the model performance as a function of probability that the rater 1 and rater 2 are in perfect agreement (TP + TN), also denoted as Po (observed probability), and, the probability (expected) both the raters are in agreement by chance or randomly, denoted as Pe in the following formula.
Now that we have defined the terms, let’s calculate the Cohen Kappa score. Let the total observation (TP + FP + FN + TN) is N. Or, N = TP + FP + FN + TN
The first step is to calculate the probability that both the raters are in perfect agreement:
Observed Agreement, Po = (TP + TN) / N
In our example, this would be:
Po = (45+15)/100=0.6
Next, we need to calculate the expected probability that both the raters are in agreement by chance. This is calculated by multiplying the expected probability that both the raters are in agreement that the classes are positive, and, the classes are negative.
Pe = [{Pe(rater 1 says Yes) / N}* {Pe(rater 2 says Yes) / N} + [{Pe(rater 1 says no) / N} * {Pe(rater 2 says no) / N}]
So in our case this would be calculated as:
Pe = 0.7 x 0.6 + 0.4 x 0.3 = 0.42 + 0.12 = 0.54
Now that we have both the observed and expected agreement, we can calculate Cohen’s Kappa:
Kappa score = (Po – Pe) / (1 – Pe)
In our example, this would be:
K = (0.6 – 0.54)/(1 – 0.54)= 0.06 / 0.46 = 0.1304 or a little over 13%
Kappa can range from 0 to 1. A value of 0 means that there is no agreement between the raters (real-world observer vs classification model), and a value of 1 means that there is perfect agreement between the raters. In most cases, anything over 0.7 is considered to be very good agreement.
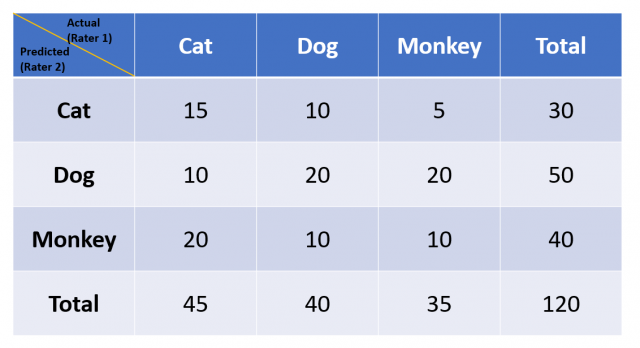
Cohen Kappa score can also be used to assess the performance of multi-class classification model. Lets take a look at the following confusion matrix representing a image classification model (CNN model) which classifies image into three different classes such as cat, dog and monkey.
Lets calculate the Kappa score for the above confusion matrix representing multiclass classification model:
Po = (15 + 20 + 10) / 120 = 45/120 = 0.375
Pe = 45*30/120*120 + 40*50/120*120 + 35*40/120*120
= 0.09375 + 0.1389 + 0.09722 = 0.32987
K = (P0 – Pe) / (1 – Pe) = (0.375 – 0.32987) / (1 – 0.32987) = 0.04513 / 0.67013
= 0.0673
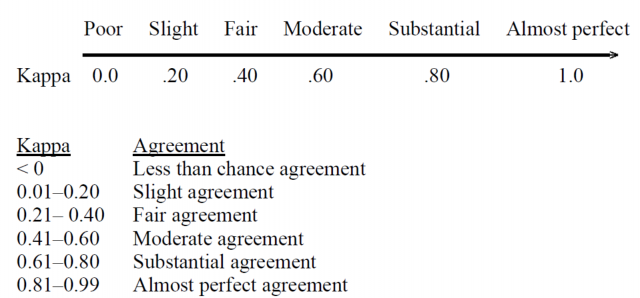
Interpretation of the Kappa Score or Coefficient
The following picture represents the interpretation of Cohen Kappa Score:
There are a few things to keep in mind when interpreting Kappa values:
- Kappa is sensitive to changes in the distribution of ratings. For example, if there is a small number of ratings in one category and a large number in another, Kappa will be artificially inflated.
- Kappa is also sensitive to imbalanced datasets, where one class is much more frequent than another. In these cases, it’s often better to use a metric like F-measure that isn’t as sensitive to class imbalance.
- Kappa values can be negative, which indicates less agreement than would be expected by chance alone.
- A value of 0 indicates that there is no agreement between the raters, and a value of 1 indicates perfect agreement between the raters.
Python code example to calculate Cohen’s Kappa Score
Python Sklearn.metrics module provides cohen_kappa_score function for calculating the Kappa score or coefficient. The following is the python code example of how to calculate the Kappa score.
from sklearn.metrics import cohen_kappa_score
#define array of ratings for both raters
rater1 = [0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0]
rater2 = [0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0]
#calculate Cohen's Kappa
cohen_kappa_score(rater1, rater2)
The Cohen Kappa score comes out to be 0.21053
Cohen Kappa Scoring can also be used with cross validation technique as a custom scorer. The following is how Cohen Kappa scoring can be used with cross_val_score, which is a utility function provided by Python Sklearn to evaluate the performance of a model by cross-validation. In the following code, notice the code, scoring=make_scorer(cohen_kappa_score). This specifies that the scoring mechanism for evaluating the model should be the Cohen’s Kappa Score.
from sklearn.metrics import make_scorer
print(cross_val_score(lr_model,
features,
targets,
scoring=make_scorer(cohen_kappa_score),
n_jobs=-1).mean())
In above code, essentially, the code is using cross-validation to assess the average Cohen’s Kappa Score of the logistic regression model (lr_model) across different splits of the data. This provides a more generalized view of the model’s performance, particularly in terms of how well it agrees with the true outcomes, corrected for chance agreement. This is especially useful in situations where class imbalance might make simple accuracy an unreliable metric.
Conclusion
Cohen Kappa Score is a statistic used to measure the agreement between two raters. It can be used to calculate how much agreement there is between raters on a scale from 0-1, with 1 being perfect agreement and 0 being no agreement at all. The higher the score, the more agreement there is between the raters. Cohen Kappa score or Kappa coefficient is used for assessing the performance of machine learning classification models. Cohen Kappa Score is most commonly used in research settings, but it can also be applied to other fields like marketing. Let us know if you have any questions about Cohen Kappa Score or how it can be applied in your field.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com
- MSE vs RMSE vs MAE vs MAPE vs R-Squared: When to Use? - April 25, 2024
- Gradient Descent in Machine Learning: Python Examples - April 22, 2024
- Loss Function vs Cost Function vs Objective Function: Examples - April 19, 2024
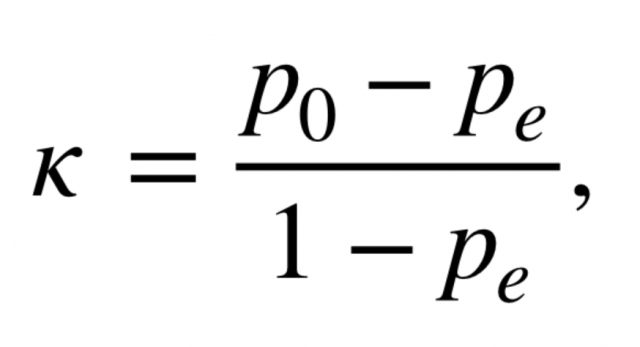
I think the Pe where the 3×3 contingency table is miscalculated
Thank you for pointing out correctly. Corrected!