In the field of computer vision and deep learning, convolutional neural networks (CNNs) are widely used for image recognition tasks. A fundamental building block of CNNs is the convolutional layer, which extracts features from the input image by convolving it with a set of learnable filters. However, another type of layer called transposed convolution, also known as deconvolution, has gained popularity in recent years. In this blog post, we will compare and contrast these two types of layers, provide examples of their usage, and discuss their strengths and weaknesses.
What are Convolutional Layer? What’s their purpose?
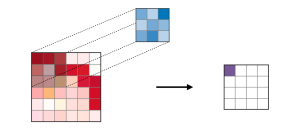
A convolutional layer is a fundamental building block of a convolutional neural network (CNN). It performs a mathematical operation called convolution on the input data, which is typically an image. The layer makes use of filters, also known as kernels or weights, that slide over the input data and perform a dot product operation between the filter values and the corresponding pixel values in the input. The result of this operation is a set of output feature maps, which represent the learned features of the input data. The following is a representation of how filter slide over the image which results into the feature map.
Let’s understand this with an example. The following represents a 3 x 3 input image, 2 x 2 filter / kernel and we get a feature map of 2 x 2 matrix.
Input image (I):
[1 2 3
4 5 6
7 8 9]
Filter/kernel (K):
[1 2
3 4]
Output feature map:
[37 47
67 77]
Let’s understand how does the convolution work. First and foremost, the filter when slid over the input image will result in dot product of filter with 2 x 2 matrix in image represented using following. Check and validate using above data.
[1 2
4 5]
The dot product results in the first element of feature map which is 19. Here is the representation of dot product.
1*1 + 2*2 + 3*4 + 4*5 = 1 + 4 + 12 + 20 = 37
Similarly, other elements of feature map would look like the following when the filter is slid over 2 x 2 matrix of input matrix.
1*2 + 2*3 + 3*5 + 4*6 = 2 + 6 + 15 + 24 = 47
1*4 + 2*5 + 3*7 + 4*8 = 4 + 10 + 21 + 32 = 67
1*5 + 2*6 + 3*8 + 4*9 = 5 + 12 + 24 + 36 = 77
Thus, the resultant feature map becomes the following as given above as well:
[37 47
67 77]
Now that we understood what’s the convolutional layer and how does the convolution operation works, lets understand what’s the purpose of having convolutional layer.
Convolutional layers are used extensively in computer vision tasks such as image recognition, object detection, and segmentation. They are particularly well-suited to these tasks because they can learn to recognize features such as edges, corners, and textures, which are important for distinguishing between different objects in an image. Additionally, convolutional layers are able to automatically learn hierarchical representations of features, meaning that lower-level features (e.g., edges) are combined to form higher-level features (e.g., shapes). This hierarchical representation enables CNNs to achieve state-of-the-art performance on many computer vision tasks.
The convolutional layer was originally developed to address a fundamental limitation of traditional artificial neural networks, which are fully connected and treat all input features as independent. This approach is not well-suited to processing images and other high-dimensional inputs, which contain spatial structures and correlations between nearby pixels or regions.
What are Convolutional Transpose Layers? What’s their purpose?
A convolutional transpose layer, also known as a transposed convolution or deconvolutional layer, is a type of layer in a neural network that performs an inverse operation to the convolutional layer. Whereas the convolutional layer takes an input image and produces a smaller output feature map, the transposed convolutional layer takes an input feature map and produces a larger output image.
The transposed convolution can be defined as an operation that can be used in encoder decoder network architectures to increase the spatial resolution of feature maps. It is often used in tasks such as image segmentation, image synthesis, etc. In a regular convolution operation, the input image is convolved with a set of learnable filters to produce a set of feature maps. Transposed convolution, on the other hand, takes the feature maps and learns how to “undo” the convolution, effectively increasing the resolution of the feature maps.
Lets understand with an example of performing transposed convolution with stride = 1 and no padding with the help of following example:
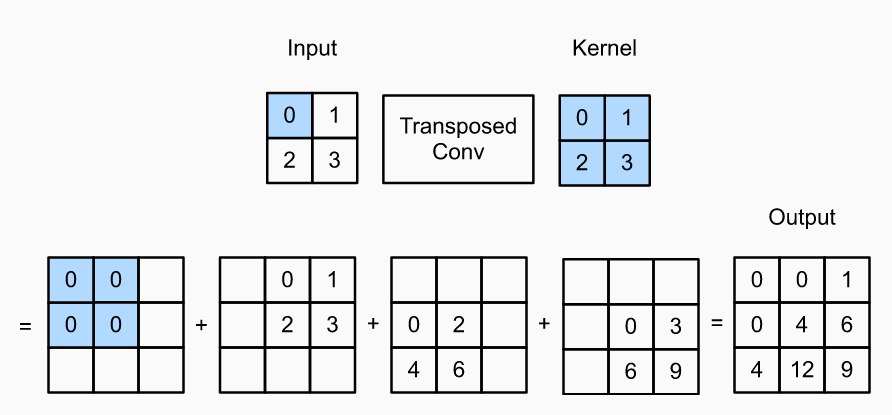
Let’s understand the transposed convolution with the help of input feature map of size 2 x 2 and kernel / filter of size 2 x 2.
- When the input feature map is of size N x N and convolution filter of size F x F, the output feature map that gets created after transposed convolution is of size (N + F – 1) x (N + F – 1) and gets initialized with zeros. Thus, in the above example, the output feature map will be of size (2 + 2 – 1) x (2 + 2 -1) = 3 x 3.
- To arrive at the above output, we applied each filter to the padded feature map by sliding it over the input, and perform element-wise multiplication. For each intermediate tensor, each element in the input tensor is multiplied by the kernel so that the resulting F x F tensor replaces a portion in each intermediate tensor.
- For example, 0 (shaded with blue in input tensor) gets multiplied with all the elements in kernel and the output shows up in the intermediate tensor as [0 0 0 0].
- Similarly, 1 from input gets multiplied with all the elements in kernel and that results in the output [0 1 2 3] in the intermediate tensor.
- 2 from input gets multiplied with all the elements in kernel and that results in the output [0 2 4 6] in the intermediate tensor.
- 3 from input gets multiplied with all the elements in kernel and that results in the output [0 3 6 9] in the intermediate tensor.
- When all of the intermediate tensors get added, it results in the output tensor as [[0 0 1][0 4 6][4 12 9]
- Stride = 1 means that the filter slides over the input one pixel at a time.
- The resulting output feature map will have size (N + F – 1)x(N + F – 1)
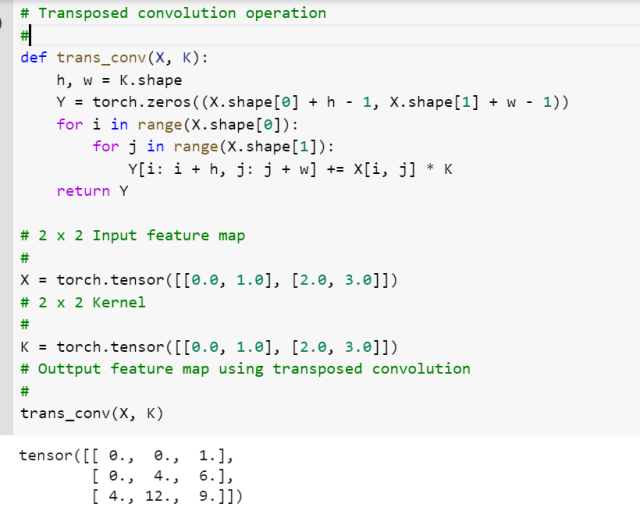
The following code represents transposed convolution:
import torch
# Transposed convolution operation
#
def trans_conv(X, K):
h, w = K.shape
Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1))
for i in range(X.shape[0]):
for j in range(X.shape[1]):
Y[i: i + h, j: j + w] += X[i, j] * K
return Y
# 2 x 2 Input feature map
#
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
#
# 2 x 2 Kernel
#
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
#
# Outtput feature map using transposed convolution
#
trans_conv(X, K)
Conclusion
In this blog, we discussed discusses the differences between the convolution layer and the transposed convolution layers. The convolution layer is a fundamental operation in image processing, and it involves convolving an image with a filter to produce a new feature map. On the other hand, the transposed convolution layer is used in encoder – decoder based neural networks to reconstruct an image from a feature map. The primary difference between these two types of layers is that convolutional layers reduce the size of the image, while transposed convolutional layers increase the size of the image. Please feel free to leave a comment or question in the comment section of the blog post if you have any further inquiries.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me