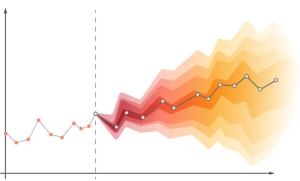
Time-series forecasting is a specific type of forecasting / predictive modeling that uses historical data to predict future trends in a particular time series. There are several different metrics that can be used to measure the accuracy and efficacy of a time-series forecasting model, including Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and others. By understanding these performance metrics, you can better assess the effectiveness of your time-series forecasting model and make necessary adjustments as needed. In this blog, you will learn about the different time-series forecasting model performance metrics and how to use them for model evaluation. Check out a related post – Different types of time-series forecasting models
Performance metrics for evaluating a time-series forecasting model
There are several different performance metrics that can be used to measure the accuracy and efficacy of a time-series forecasting model, including Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and others. By understanding these performance metrics, you can better assess the effectiveness of your time-series forecasting model and make necessary adjustments as needed.
- Root Mean Squared Error (RMSE) is the most common metric used to measure the accuracy of a time-series forecasting model. It is calculated by taking the square root of the mean of the squared differences between the actual values and the predictions of the model. RMSE is often reported in units of “error per unit,” which allows you to compare different models on an equal footing. The question that many ask is what should be appropriate RMSE value for time-series forecasting model? Well, there is no definitive answer to this question, as the appropriate RMSE value will vary depending on the specific data and forecasting model. However, a good rule of thumb is that RMSE should be as low as possible, while still maintaining a high level of accuracy. To calculate RMSE, you first need to calculate the error for each data point. This can be done by taking the difference between the actual value and the prediction of the model. You then need to square these errors and take the mean of them. This output is also called as Mean Square Error (MSE). Finally, you need to take the square root of this mean to get the RMSE value. The below represents the formula for calculating RMSE value
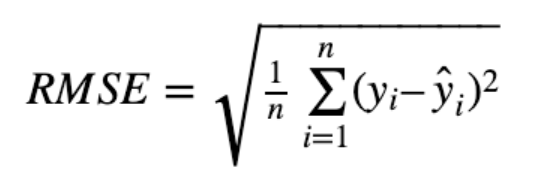
- Mean Absolute Error (MAE) is another common metric used to measure the accuracy of a time-series forecasting model. It is also called Mean Absolute Deviation (MAD). It is calculated by taking the average of the absolute differences between the actual values and the predictions of the model. What should be the most appropriate value of MAE for the time-series forecasting model. There is no definitive answer to what should be the appropriate MAE value for a time-series forecasting model. However, a good rule of thumb is that MAE should be as low as possible, while still maintaining a high level of accuracy. In general, you should aim for an MAE value of less than 1.0 for time-series forecasting models. The below represents the formula for calculating MAE value
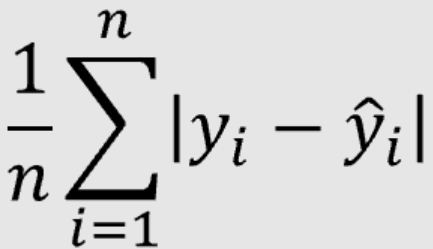
MSE is the mean squared error between the actual and predicted values, while MAE is the mean absolute error between the actual and predicted values. MSE is a more accurate measure of forecasting error than MAE, as it takes into account the magnitude of the errors. MSE penalizes the large deviation between the actual and predicted value.
Conclusion
In this blog post, you have learned about the different performance metrics used for evaluating time-series forecasting models. You have also learned about the importance of Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE), and how to calculate them. By understanding these metrics, you can better assess the accuracy of your time-series forecasting model and make necessary adjustments as needed.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me