In this post, you will learn about Java implementation for Rosenblatt Perceptron.
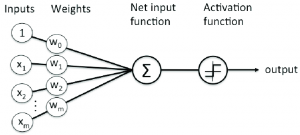
Rosenblatt Perceptron is the most simplistic implementation of neural network. It is also called as single-layer neural network. The following diagram represents the Rosenblatt Perceptron:
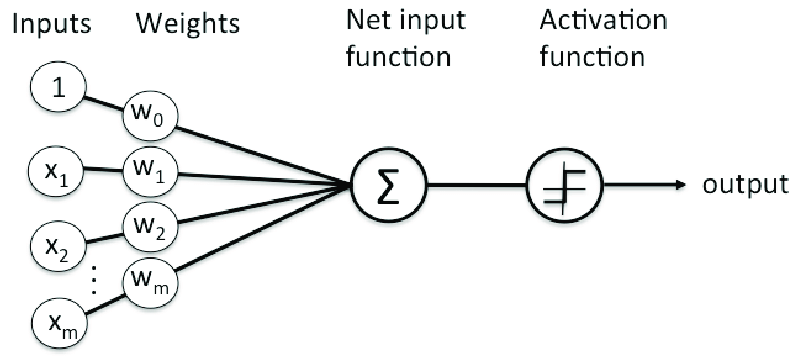
Fig1. Perceptron
The following represents key aspect of the implementation which is described in this post:
- Method for calculating “Net Input“
- Activation function as unit step function
- Prediction method
- Fitting the model
- Calculating the training & test error
Method for calculating “Net Input”
Net input is weighted sum of input features. The following represents the mathematical formula:
$$Z = {w_0}{x_0} + {w_1}{x_1} + {w_2}{x_2} + … + {w_n}{x_n}$$
In the above equation, w0, w1, w2, …, wn represents the weights for the features such as x0, x1, x2, …, xn respectively. Note that x0 takes the value of 1 is used to represent the bias.
The above could be achieved using the following Java code:
public double netInput(double[] input) {
double netInput = 0;
netInput += this.weights[0];
for(int i = 0; i < input.length; i++) {
netInput += this.weights[i+1]*input[i];
}
return netInput;
}
Activation Function as Unit Step Function
For Rosenblatt Perceptron, the activation function is same as a unit step function which looks like the following:
- If the value of net input is greater than or equal to zero, assign 1 as the class label
- If the value of net input is less than zero, assign -1 as the class label
In above, the net input, represented as Z, also includes the bias element as depicted by w0x0 in the following equation:
$$Z = {w_0}{x_0} + {w_1}{x_1} + {w_2}{x_2} + … + {w_n}{x_n}$$
Mathematically, the activation function gets represented as the following unit step function:
$$ \phi(Z) = 1 if Z \geq 0 $$
$$ \phi(Z) = -1 if Z < 0 $$
The following code represents the activation function:
private int activationFunction(double[] input) {
double netInput = this.netInput(input);
if(netInput >= 0) {
return 1;
}
return -1;
}
Prediction Method
For Rosenblatt Perceptron, the prediction method is same as the activation function. If the weighted sum of input is greater than equal to 0, the class label is assigned as 1 or else -1.
The following code represents the prediction method:
public int predict(double[] input) {
return activationFunction(input);
}
Model Fitting
Fitting the model requires the following to happen:
- Initialize the weights
- Loop for N where N is number of iterations which can be set during creating Perceptron object
- For every training record, do the following:
- Calculate the value of activation function
- Calculate the value of weight updates as a function of true value, activation function value, input and learning rate
- Update each of the weight
- Calculate the error for each of the iteration
- For every training record, do the following:
The following code represents the above algorithm:
public void fit(double[][] x, double[] y) {
//
// Initialize the weights
//
Random rd = new Random();
this.weights = new double[x[0].length + 1];
for(int i = 0; i < this.weights.length; i++) {
this.weights[i] = rd.nextDouble();
}
//
// Fit the model
//
for(int i = 0; i < this.noOfIteration; i++) {
int errorInEachIteration = 0;
for(int j=0; j &lt; x.length; j++) {
//
// Calculate the output of activation function for each input
//
double activationFunctionOutput = activationFunction(x[j]);
this.weights[0] += this.learningRate*(y[j] - activationFunctionOutput);
for(int k = 0; k &lt; x[j].length; k++) {
//
// Calculate the delta weight which needs to be updated
// for each feature
//
double deltaWeight = this.learningRate*(y[j] - activationFunctionOutput)*x[j][k];
this.weights[k+1] += deltaWeight;
}
//
// Calculate error for each training data
//
if(y[j] != this.predict(x[j])) {
errorInEachIteration++;
}
}
//
// Update the error in each Epoch
//
this.trainingErrors.add(errorInEachIteration);
}
}
Training & Test Error Calculation
Once the model is fit, one should be able to calculate training and test error. Training error is total misclassifications recorded during the training (across all the iterations/epochs). Test error is misclassification for the test data.
In the code under model fitting, note how errorInEachIteration is incremented for every training record that gets misclassified and trainingError is updated in each iteration.
Source Code
The source code can be found in on this GitHub page for Perceptron.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me