In machine learning and data analysis, it is often necessary to identify patterns and clusters within large sets of data. However, traditional clustering algorithms such as k-means clustering have limitations when it comes to identifying clusters with different shapes and sizes. This is where Gaussian mixture models (GMMs) come in. But what exactly are GMMs and when should you use them?
Gaussian mixture models (GMMs) are a type of machine learning algorithm. They are used to classify data into different categories based on the probability distribution. Gaussian mixture models can be used in many different areas, including finance, marketing and so much more! In this blog, an introduction to gaussian mixture models is provided along with real-world examples, what they do and when GMMs should be used.
What are Gaussian Mixture Models (GMM)?
Gaussian mixture models (GMM) are a probabilistic concept used to model real-world data sets. GMMs are a generalization of Gaussian distributions and can be used to represent any data set that can be clustered into multiple Gaussian distributions. The Gaussian mixture model is a probabilistic model that assumes all the data points are generated from a mix of Gaussian distributions with unknown parameters. A Gaussian mixture model can be used for clustering, which is the task of grouping a set of data points into clusters.
GMMs can be used to find clusters in data sets where the clusters may not be clearly defined. Additionally, GMMs can be used to estimate the probability that a new data point belongs to each cluster. Gaussian mixture models are also relatively robust to outliers, meaning that they can still yield accurate results even if there are some data points that do not fit neatly into any of the clusters. This makes GMMs a flexible and powerful tool for clustering data.
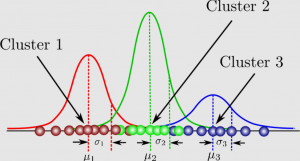
The Gaussian mixture model can be understood as a probabilistic model where Gaussian distributions are assumed for each group and they have means and covariances which define their parameters. GMM consists of two parts – mean vectors (μ) & covariance matrices (Σ). Recall that a Gaussian distribution is defined as a continuous probability distribution that takes on a bell-shaped curve. Another name for Gaussian distribution is the normal distribution.
Here is a picture of Gaussian mixture models:
GMM has many applications, such as density estimation, clustering, and image segmentation. For density estimation, GMM can be used to estimate the probability density function of a set of data points. For clustering, GMM can be used to group together data points that come from the same Gaussian distribution. And for image segmentation, GMM can be used to partition an image into different regions.
Gaussian mixture models can be used for a variety of use cases, including identifying customer segments, detecting fraudulent activity, and clustering images. In each of these examples, the Gaussian mixture model is able to identify clusters in the data that may not be immediately obvious. As a result, Gaussian mixture models are a powerful tool for data analysis and should be considered for any clustering task.
What is the expectation-maximization (EM) method in relation to GMM?
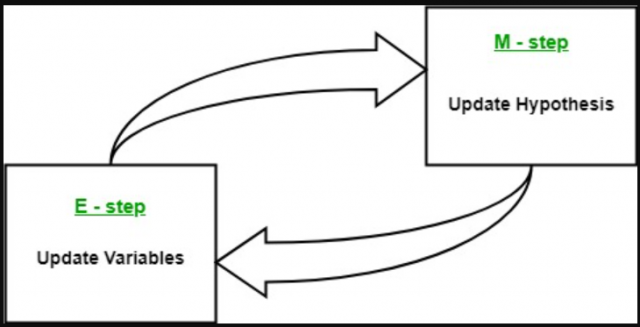
In Gaussian mixture models, an expectation-maximization method is a powerful tool for estimating the parameters of a Gaussian mixture model (GMM). The expectation is termed E and maximization is termed M. Expectation is used to find the Gaussian parameters which are used to represent each component of gaussian mixture models. Maximization is termed M and it is involved in determining whether new data points can be added or not.
The expectation-maximization method is a two-step iterative algorithm that alternates between performing an expectation step, in which we compute expectations for each data point using current parameter estimates and then maximize these to produce a new gaussian, followed by a maximization step where we update our gaussian means based on the maximum likelihood estimate. The EM method works by first initializing the parameters of the GMM, then iteratively improving these estimates. At each iteration, the expectation step calculates the expectation of the log-likelihood function with respect to the current parameters. This expectation is then used to maximize the likelihood in the maximization step. The process is then repeated until convergence. Here is a picture representing the two-step iterative aspect of the algorithm:
What are the key steps of using Gaussian mixture models for clustering?
The following are three different steps to using gaussian mixture models:
- Determining a covariance matrix that defines how each Gaussian is related to one another. The more similar two Gaussians are, the closer their means will be and vice versa if they are far away from each other in terms of similarity. A gaussian mixture model can have a covariance matrix that is diagonal or symmetric.
- Determining the number of Gaussians in each group defines how many clusters there are.
- Selecting the hyperparameters which define how to optimally separate data using gaussian mixture models as well as deciding on whether or not each gaussian’s covariance matrix is diagonal or symmetric.
What are the differences between Gaussian mixture models and other types of clustering algorithms such as K-means?
Here are some of the key differences between Gaussian mixture models and the K-means algorithm used for clustering:
- A Gaussian mixture model is a type of clustering algorithm that assumes that the data point is generated from a mixture of Gaussian distributions with unknown parameters. The goal of the algorithm is to estimate the parameters of the Gaussian distributions, as well as the proportion of data points that come from each distribution. In contrast, K-means is a clustering algorithm that does not make any assumptions about the underlying distribution of the data points. Instead, it simply partitions the data points into K clusters, where each cluster is defined by its centroid.
- While Gaussian mixture models are more flexible, they can be more difficult to train than K-means. K-means is typically faster to converge and so may be preferred in cases where the runtime is an important consideration.
- In general, K-means will be faster and more accurate when the data set is large and the clusters are well-separated. Gaussian mixture models will be more accurate when the data set is small or the clusters are not well-separated.
- Gaussian mixture models take into account the variance of the data, whereas K-means does not.
- Gaussian mixture models are more flexible in terms of the shape of the clusters, whereas K-means is limited to spherical clusters.
- Gaussian mixture models can handle missing data, whereas K-means cannot. This difference can make Gaussian mixture models more effective in certain applications, such as data with a lot of noise or data that is not well-defined.
What are the scenarios when Gaussian mixture models can be used?
The following are different scenarios when GMMs can be used:
- Gaussian mixture models can be used in a variety of scenarios, including when data is generated by a mix of Gaussian distributions when there is uncertainty about the correct number of clusters, and when clusters have different shapes. In each of these cases, the use of a Gaussian mixture model can help to improve the accuracy of results. For example, when data is generated by a mix of Gaussian distributions, using a Gaussian mixture model can help to better identify the underlying patterns in the data. In addition, when there is uncertainty about the correct number of clusters, the use of a Gaussian mixture model can help to reduce the error rate.
- Gaussian mixture models can be used for anomaly detection; by fitting a model to a dataset and then scoring new data points, it is possible to flag points that are significantly different from the rest of the data (i.e. outliers). This can be useful for identifying fraud or detecting errors in data collection.
- In the case of time series analysis, GMMs can be used to discover how volatility is related to trends and noise which can help predict future stock prices. One cluster could consist of a trend in the time series while another can have noise and volatility from other factors such as seasonality or external events which affect the stock price. In order to separate out these clusters, GMMs can be used because they provide a probability for each category instead of simply dividing the data into two parts such as that in the case of K-means.
- Another example is when there are different groups in a dataset and it’s hard to label them as belonging to one group or another which makes it difficult for other machine learning algorithms such as the K-means clustering algorithm to separate out the data. GMMs can be used in this case because they find Gaussian mixture models that best describe each group and provide a probability for each cluster which is helpful when labeling clusters.
- Gaussian mixture models can generate synthetic data points that are similar to the original data, they can also be used for data augmentation.
What are some real-world examples where Gaussian mixture models can be used?
There are many different real-world problems that can be solved with gaussian mixture models. Gaussian mixture models are very useful when there are large datasets and it is difficult to find clusters. This is where Gaussian mixture models help. It is able to find clusters of Gaussians more efficiently than other clustering algorithms such as k-means.
Here are some real-world problems which can be solved using Gaussian mixture models:
- Finding patterns in medical datasets: GMMs can be used for segmenting images into multiple categories based on their content or finding specific patterns in medical datasets. They can be used to find clusters of patients with similar symptoms, identify disease subtypes, and even predict outcomes. In one recent study, a Gaussian mixture model was used to analyze a dataset of over 700,000 patient records. The model was able to identify previously unknown patterns in the data, which could lead to better treatment for patients with cancer.
- Modeling natural phenomena: GMM can be used to model natural phenomena where it has been found that noise follows Gaussian distributions. This model of probabilistic modeling relies on the assumption that there exists some underlying continuum of unobserved entities or attributes and that each member is associated with measurements taken at equidistant points in multiple observation sessions.
- Customer behavior analysis: GMMs can be used for performing customer behavior analysis in marketing to make predictions about future purchases based on historical data.
- Stock price prediction: Another area Gaussian mixture models are used is in finance where they can be applied to a stock’s price time series. GMMs can be used to detect changepoints in time series data and help find turning points of stock prices or other market movements that are otherwise difficult to spot due to volatility and noise.
- Gene expression data analysis: Gaussian mixture models can be used for gene expression data analysis. In particular, GMMs can be used to detect differentially expressed genes between two conditions and identify which genes might contribute toward a certain phenotype or disease state.
Gaussian mixture models are a type of machine learning algorithm that is commonly used in data science. They can be applied to different scenarios, including when there are large datasets and it’s difficult to find clusters or groups of Gaussians. Gaussian mixture models provide probability estimates for each cluster which allows you to label the clusters with less effort than k-means clustering algorithms would require. GMMs also offer some other benefits such as finding Gaussian mixture models that best describe each group, helping identify underlying categories of data sets, and predicting future stock prices more accurately by considering volatility and noise factors. If you’re looking for an efficient way to find patterns within complicated datasets or need help modeling natural phenomena like natural disasters or customer behavior analysis in your marketing, gaussian mixture models could be the right choice.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me