In linear regression, dummy variables are used to represent the categorical variables in the model. There are a few different ways that dummy variables can be created, and we will explore a few of them in this blog post. We will also take a look at some examples to help illustrate how dummy variables work. We will also understand concepts related to the dummy variable trap. By the end of this post, you should have a better understanding of how to use dummy variables in linear regression models. As a data scientist, it is important to understand how to use linear regression and dummy variables.
What are dummy variables in linear regression models?
While training linear regression models, if all of the predictor variables are quantitative or numerical in nature, it does not pose any problem. However, if there are one or more predictor variables that are categorical in nature, that’s where the challenge comes in. For example, consider a linear regression model to predict the price of a house. Some of the predictor variables in the model could be the size of the house, number of bedrooms, number of bathrooms, location, etc. While size and number of bedrooms are numerical variables that can take on any value, location is a categorical variable. It could take on values like the city center, suburbs, countryside, etc. In order to use this categorical variable in the linear regression model, we need some mechanism. This is where dummy variables come into the picture.
Dummy variables are often used in linear regression models to represent categorical variables or qualitative variables. Consider a scenario when a predictor variable has only two possible values. For example, let’s say there is a predictor variable such as does_smoke which has only two possible values such as the person smokes or does not smoke. For such a scenario, a variable known as a dummy variable is created which takes on values such as the following:
does_smoke = 1 if the person smokes and 0 if the person does not smoke.
Based on the above the model is trained and linear regression is applied. One can also use another coding scheme such as -1 and 1 instead of 0/1. Thus, the following can also hold good:
does_smoke = 1 if the person smokes and -1 if the person does not smoke.
Dummy variables are also used when there are more than two possible values for a predictor variable. The technique is called one-hot encoding. In this technique, a new dummy variable is created for each unique value of the predictor variable. For a particular record, the value of one except all dummy variables will be 1. The ordering of dummy variables doesn’t matter. This is also demonstrated in the previous example in relation to gender having value such as male or female. For example, let’s say we have a variable such as education that can take on the following values:
- High school
- Graduate
- Post-graduate
In this case, we will create three dummy variables for three unique values of education such as high school, graduate, and post-graduate. At any point in time, only one of the dummy variables shown below will be having the value of 1. Others will have the 0 value.
- is_high_school = 1 if the person is in high school and 0 otherwise
- is_college = 1 if the person is in college and 0 otherwise
- is_university = 1 if the person is in university and 0 otherwise
One-hot encoding has advantages over other techniques for creating dummy variables.
- One advantage is that it avoids problems that can occur when using linear regression with categorical variables that have a natural ordering.
- Another advantage is that the interpretation of the regression coefficients is more straightforward when using one-hot encoding.
Dummy Variable Trap
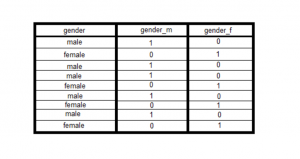
A dummy variable trap is defined as the scenario when you include all the dummy variables in the linear regression model even though some of the dummy variables are highly correlated. This leads to multicollinearity. For example, let’s say that the gender can have dummy variables such as the following:
- is_male (1 is male, 0 otherwise)
- is_female (1 is female, 0 otherwise)
Given that gender can only take above two values, you may note that if the value of is_male is 0, one can predict the value of is_female as 1. This results in redundancy. To avoid this issue, one of the dummy variables such as is_male or is_female can be dropped from the linear regression model.
Dummy Variables in Python
The following represents some of the techniques one can use to transform categorical variables into numerical ones using dummy variables in Python.
- One-hot encoding: pandas get_dummies() function. You can also use OneHotEncoder or sklearn.preprocessing module. Here is a detailed post on one-hot encoding concepts and python code example.
- Label encoding: scikit-learn’s LabelEncoder class. Check out my post on LabelEncoder.
- Binary encoding: scikit-learn’s LabelBinarizer class
Dummy Variables in R
The following represents some of the techniques one can use to transform categorical variables into numerical ones using dummy variables in R.
- One-hot encoding: caret’s dummyVars() function
- Label encoding: model.matrix() function and factor() function
- Binary encoding: model.matrix() function
Dummy variables are used in linear regression models to represent categorical variables or qualitative variable. In linear regression, dummy variables are used to represent the categorical variables in the model. There are a few different ways that dummy variables can be created, and we explored a few of them in this blog post. One should also pay attention to dummy variable trap when working with dummy variables for training regression models. We also looked at some examples to help illustrate how dummy variables work including functions from Python and R. In case you have further questions, please feel free to reach out!
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me