Dummies Notes – What is B-Tree and Why Use Them?

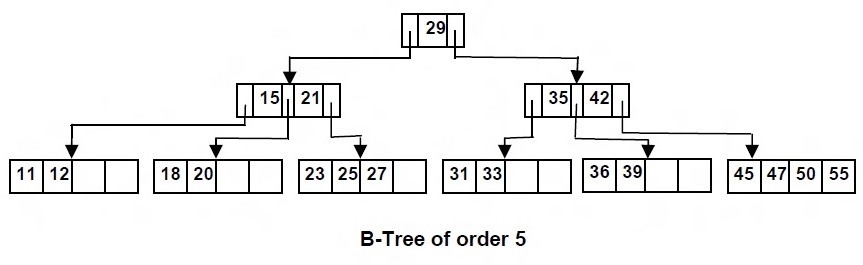
Simply speaking, B-Tree is nothing but the generalization of a Binary Search Tree. One may recall that the nodes in a Binary Search Tree could have just one key and a maximum of two child nodes. However, a B-Tree could have nodes having multiple keys (more than one) and, more than two child nodes. Following diagram represents a B-Tree of order 5.

B-Tree

Following are some of the key points discussed later in this article:

• Key Features of B-Tree
• Why use B-Tree?
• Insertion into B-Tree
• Reading references on B-Trees

Key Features of B-Tree

Following represents features of B-Tree:

• B-Tree is a self-balancing tree. All leaf nodes are at the same level. Alternatively, each path from the root to a leaf node has same length.
• Order of the B-Tree is defined as the maximum number of child nodes that each node could have or point to. In the above diagram, the order is 5.
• The maximum number of keys that each node could have is (M – 1) where M is order of the tree. In above diagram, the maximum number of keys that could be stored is 4.
• Each internal nodes’ keys act as separation values which divides its subtrees. For example, in above diagram, lets take node with keys as 15 and 21. The referred node has three child nodes. All values in the leftmost subtree will be less than 15 (which is 11 and 12), all values in the middle subtree will be between 15 and 21 (which is 18 and 20), and all values in the rightmost subtree will be greater than 21 (which is 23, 25 and 27).
• Root node is either a leaf or, would have at least two children. Do confirm this with above diagram.
• Internal nodes (niether root nor leaf nodes) have between between M/2 and M child nodes given M is the order of the tree. This helps in avoiding the wastage of space in each node and, thus, the skewed distribution.
• Data in each node is sorted by the keys, for sequential traversing.
• Maximum number of items that could be stored in a B-Tree of order M and height H is one less than M raised to H.

Why use B-Tree?

• To Create Indexes in RDBMS Databases
  Many RDBMS databases use B-Tree for storing index data. Most indexes are too large to fit into memory and thus, they need to be stored onto disk. With that, following disadvantages creep in owing to the data storage on the disk if data structures like array are used:
  • Large number of disk hops (and hence greater time required to read) to access the requisite data as only a chunk of data could fit in a disk block of predefined size limit.
  • Rearrange the array in case the data needs to be inserted or deleted in the sorted manner
  • Inefficient searching operation

  Thus, given some of the above disadvantages, what is needed is a data structure which achieves the primary objectives of faster search, faster sequential access and, faster insertion and deletion operations. This is where B-Tree fits in. Following is how indexes get stored and searched in the B-Tree.

  • The root, each internal node, and each leaf is typically stored in a disk block.
  • Index data is stored in appropriate disk block (leaf node) based on the key information.
  • In order to search any item in the index, one may require to traverse to the root node, appropriate internal node and then the leaf node. Once found the most appropriate leaf node, the index data would then be found into that disk block.
  • With B+-Trees, large number of keys could be stored in root and internal nodes thereby reducing lesser number of I/Os.
  • One may note that it reduces the number of disk accesses by a very significant number and hence achieve a lot faster operation.
• For efficient and faster random/sequential read/write access. This applies to requirements such as storing large amount of data and searching for a particular term thereafter.

Insertion into B-Tree

A key is always inserted into the leaf node of the B-Tree. However, to make sure that all leaf remains at the same level, the tree grows upward adding nodes at a level lesser than the level of the leaf node. Following is how the insertion happens in the B-Tree given that there is only a root node present in the B-Tree.

• Insertion of Keys in Root Node
  • If the number of key in the root node is less than (M-1) keys, the key is added appropriately in the sorted manner.
  • Once the root node is full, the root node splits into two nodes. The median value is kept in the root node, and rest of the values are moved into child nodes based on the condition that values less than the median value goes to left child node and values greater than median value goes to right child node.
• Insertion of Keys in Non-Root Node
  • When a key needs to be inserted in non-root node, if the node has number of keys lesser than (M-1) keys, the key is inserted in sorted manner in the node
  • In case the node is full, the node is split into two nodes at the same level and the middle node is moved to the parent node with the splitted nodes becoming the children nodes. In case, the parent node is also full, the key is moved further one level up and existing parent node is split into two child nodes and associated appropriately with the parent node further up by one level.
  • Splitting the nodes could propagate all the way to root node thereby creating a new level if the root is split.

Reading References for B-Trees

Following are some good pages on B-Trees that I came across on the internet:

• Memory locality & the magic of B-Trees!
• B-Tree