Type I & Type II Errors in Hypothesis Testing: Examples

This article describes Type I and Type II errors made due to incorrect evaluation of the outcome of hypothesis testing, based on a couple of examples such as the person comitting a crime, the house on fire, and Covid-19. You may want to note that it is key to understand type I and type II errors as these concepts will show up when we are evaluating a hypothesis such as those related to machine learning algorithms (linear regression, logistic regression, etc). For example, in the case of linear regression models, the significance value is compared with the p-value and, the null hypothesis that the parameter/coefficient is equal to zero is either rejected or failed to be rejected. You may want to check my earlier article on how to formulate a hypothesis for hypothesis testing as a precursor to understanding the concepts around Type I and Type II errors in a better manner.

Table of Contents

What is a Type I Error?

When doing hypothesis testing, one ends up incorrectly rejecting the null hypothesis (default state of being) when in reality it holds true. The probability of rejecting a null hypothesis when it actually holds good is called as Type I error. Generally, a higher Type I error triggers eyebrows because this indicates that there is evidence against the default state of being. This essentially means that unexpected outcomes or alternate hypotheses can be true. Thus, it is recommended that one should aim to keep Type I errors as small as possible. Type I error is also called as “false positive“.

Lets try and understand type I error with the help of person held guilty or otherwise given the fact that he is innocent. The claim made or the hypothesis is that the person has committed a crime or is guilty. The null hypothesis will be that the person is not guilty or innocent. Based on the evidence gathered, the null hypothesis that the person is not guilty gets rejected. This means that the person is held guilty. However, the rejection of null hypothesis is false. This means that the person is held guilty although he/she was not guilty. In other words, the innocent person is convicted. This is an example of Type I error.

In order to achieve the lower Type I error, the hypothesis testing assigns a fairly small value to the significance level. Common values for significance level are 0.05 and 0.01, although, on average scenarios, 0.05 is used. Mathematically speaking, if the significance level is set to be 0.05, it is acceptable/OK to falsely or incorrectly reject the Null Hypothesis for 5% of the time.

Type I Error & House on Fire

Whether the house is on fire?

Let’s take the example of smoke coming out of a house. There are two possibilities. Either the smoke is due to some sort of food getting cooking OR alternatively, the house is on fire. Let’s state the null hypothesis, H0, that the house is not on the fire and the smoke is mainly due to some food getting cooked. Thus, the alternate hypothesis, Ha, will be that the house is on fire.

A person passing by the house thought that the house is actually burning with fire and thus called the firefighters. However, firefighters after arriving at the spot found that the smoke was actually due to the food being cooked.

Let’s analyze the above from a statistical perspective and understand Type I error. The person passing by rejected the null hypothesis that the smoke is due to the food getting cooked and called the firefighters. However, in reality, the smoke was really due to food being cooked, and the house was not on fire. Thus, the person incorrectly or falsely rejected the null hypothesis. Or, the person raised a false alarm. Cases like these are also termed false positives. In other words, the person made a Type I Error.

Type I Error & Covid-19 Diagnosis

The symptoms of Covid-19 are actually Pneumonia like symptoms and if diagnosed late are proving fatal to life. The claim or the hypothesis is that the person is infected by Covid-19 (corona) given the Pneumonia like symptoms. Let’s state the null hypothesis that a person having symptoms of having cold and fever is not suffering from Covid-19 (in other words, he is healthy). In other words, the diagnosis of Covid-19 is negative. The alternate hypothesis is stated as the fact that the person is suffering from Covid-19 (or he is unhealthy) OR, the diagnosis comes out to be positive.

In the scenario when a person suffering from cold and fever problem opts for (or decides to take) Covid-19 diagnostic test to make sure that he isn’t suffering from Covid-19, he rejects the null hypothesis that he is healthy. However, when the test result comes out, if the person is not found to be having Covid-19, it can be called a “False Alarm” raised by the person. The person made a Type I error where he incorrectly or falsely rejected the Null Hypothesis. One may note that in cases like these when health is concerned, it is better to raise the false alarms or commit a Type I error just to make sure.

What is a Type II Error?

When doing a hypothesis testing, one fails to reject the null hypothesis when he should actually have rejected it, this error or mistake is termed as Type II error.

In case of the example related to person committing a crime, the null hypothesis is that the person is not guilty. In other words, the person is innocent. Rejecting the null hypothesis would mean that the person is guilty. Failing to reject the null hypothesis is that the person is not guilty or the null hypothesis holds good. In case, the failing to reject the null hypothesis is a mistake, this means that the person is held not guilty when he/she really was guilty.

Type II Error & House On Fire

In the above example, the null hypothesis is set as the statement that the house is not on fire and the smoke is mainly due to food being cooked and, the alternate hypothesis is the statement that the smoke is because of the fact that the house is on fire. From the above example, let’s say the passerby ignored the smoke from the house thinking that the smoke is coming out due to food being cooked. After few hours, it was found that house actually burnt. In statistical sense, the passerby failed to reject the null hypothesis that the house is not on fire and the smoke is coming due to food being cooked. Actually, the alternative hypothesis that the house is on fire was true. Cases like Type II error are also termed as False Negatives.

Type II Error & Covid-19 Diagnosis

In the case of Covid-19 example, if the person having a breathing problem fails to reject the Null hypothesis, and does not go for Covid-19 diagnostic tests when he/she should actually have rejected it. This may prove fatal to life in case the person is actually suffering from Covid-19. Type II errors can turn out to be very fatal and expensive.

Type I Error & Type II Error Explained with Diagram

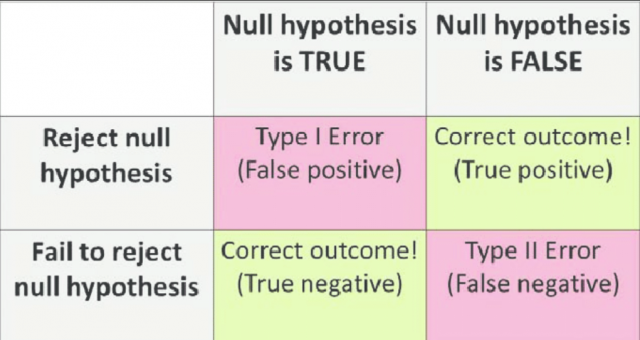
Given the diagram above, one could observe the following two scenarios:

Type I Error: When one rejects the Null Hypothesis (H0 – Default state of being) given that H0 is true, one commits a Type I error. It can also be termed as false positive.
Type II Error: When one fails to reject the Null hypothesis when it is actually false or does not hold good, one commits a Type II error. It can also be termed as a false negative.
In other cases when one rejects the Null Hypothesis when it is false or not true, and when fails to reject the Null hypothesis when it is true is the correct decision.

Type I Error & Type II Error: Trade-off

Ideally it is desired that both the Type I and Type II error rates should remain small. But in practice, this is extermely hard to achieve. There typically is a trade-off. The Type I error can be made small by only rejecting H0 if we are quite sure that it doesn’t hold. This would mean a very small value of significance level such as 0.01. However, this will result in an increase in the Type II error. Alternatively, The Type II error can be made small by rejecting H0 in the presence of even modest evidence that it does not hold. This can be obtained by having slightly higher value of significance level ssuch as 0.1. This will, however, cause the Type I error to be large. In practice, we typically view Type I errors as “bad” or “not good” than Type II errors, because the former involves declaring a scientific finding that is not correct. Hence, when the hypothesis testing is performed, What is desired is typically a low Type I error rate — e.g., at most α = 0.05, while trying to make the Type II error small (or, equivalently, the power large).

Understanding the difference between Type I and Type II errors can help you make more informed decisions about how to use statistics in your research. If you are looking for some resources on how to integrate these concepts into your own work, reach out to us. We would be happy to provide additional training or answer any questions that may arise!

Author
Recent Posts

Ajitesh Kumar

I have been recently working in the area of Data analytics including Data Science and Machine Learning / Deep Learning. I am also passionate about different technologies including programming languages such as Java/JEE, Javascript, Python, R, Julia, etc, and technologies such as Blockchain, mobile computing, cloud-native technologies, application security, cloud computing platforms, big data, etc. I would love to connect with you on Linkedin.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.

Type I & Type II Errors in Hypothesis Testing: Examples