CART Decision Tree Python Example

The Classification and Regression Tree (CART) is a supervised machine learning algorithm used for classification, regression. In this blog, we will discuss what CART decision tree is, how it works, and provide a detailed example of its implementation using Python.

What is CART & How does it work?

CART stands for Classification And Regression Tree. It is a type of decision tree which can be used for both classification and regression tasks based on non-parametric supervised learning method. The following represents the algorithm steps. First and foremost, the data is split into training and test set. 

• Take a feature K and split the training data set into two subsets based on some threshold of the feature, Tk. For example, if we are working through the IRIS data set, take a feature such as petal length, set the threshold as 2.25 cm. The question that would arise is how does the algorithm select K and Tk. The pair of K and Tk is selected in a way that purest subsets (weighted by their size) are created. This can also be called as the cost or loss function. The following cost function is optimized (minimized).
  
• Once the training set is split into two subsets, the algorithm splits the subsets into another subsets using the same logic.
• The above split continues in a recursive manner until the maximum depth (hyperparameter max_depth) is reached or the algorithm is unable to find the split that further reduces the impurity.
• The following are few other hyperparameters which can be set before the algorithm is run for training. These are used to regularize the model.
  • min_samples_split: Minimum number of samples a node must have before it is split
  • min_samples_leaf: Minimum number of samples a leaf node must have
  • max_leaf_nodes: Maximum number of leaf nodes 

CART decision tree is a greedy algorithm as it searches for optimum split right at the top most node without considering the possibility of lowest possible impurity several levels down. Note that greedy algorithms can result into a reasonably great solution but may not be optimal.

The following represents the CART cost function for regression. The cost function attempts to minimize the MSE (mean square error) for regression task. Recall that CART cost function for classification attempts to minimize impurity.

CART Decision Tree Python Example

Scikit-Learn decision tree implementation is based on CART algorithm. The algorithm produces only binary trees, e.g., non-leaf nodes always have two children. There are other algorithms such as ID3 which can produce decision trees with nodes that have more than two children.

The following is Python code representing CART decision tree classification.

import pandas as pd 

from sklearn.tree import DecisionTreeClassifier 
from sklearn.model_selection import train_test_split
from sklearn import metrics 
from sklearn import datasets 

#load IRIS dataset 
iris = datasets.load_iris() 
X = iris.data #load the features 
y = iris.target # load target variable 
  
# Split dataset into training set and test set 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)  # 70% training and 30% test 
  
# Create Decision Tree classifer object 
clf = DecisionTreeClassifier(max_depth=2)   

# Train Decision Tree Classifer 
clf = clf.fit(X_train,y_train)  

#Predict the response for test dataset  
y_pred = clf.predict(X_test)  

# Model Accuracy, how often is the classifier correct? 
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))  

You can then print the decision tree trained in the above code using the following code:

from sklearn.tree import export_graphviz
import os

# Where to save the figures
PROJECT_ROOT_DIR = "."

def image_path(fig_id):
    return os.path.join(PROJECT_ROOT_DIR, "sample_data", fig_id)

export_graphviz(
        clf,
        out_file=image_path("iris_tree.dot"),
        feature_names=iris.feature_names,
        class_names=iris.target_names,
        rounded=True,
        filled=True
    )

from graphviz import Source
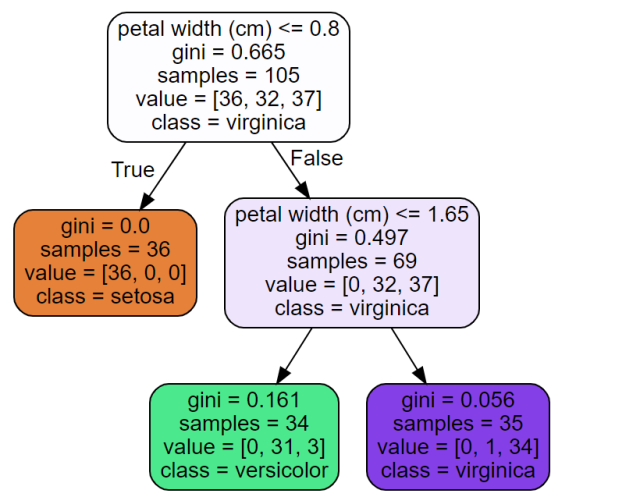
Source.from_file("./sample_data/iris_tree.dot")

Executing the above code will print the following. Recall that scikit-learn decision tree (CART) implementation always produces binary trees.

Conclusion

In conclusion, CART decision trees are powerful supervised learning algorithms that can be used for both classification and regression tasks. The loss function for CART classification algorithm is minimizing the impurity while loss function for CART regression algorithm is minimizing mean square error (MSE).

• Author
• Recent Posts

Ajitesh Kumar

I have been recently working in the area of Data analytics including Data Science and Machine Learning / Deep Learning. I am also passionate about different technologies including programming languages such as Java/JEE, Javascript, Python, R, Julia, etc, and technologies such as Blockchain, mobile computing, cloud-native technologies, application security, cloud computing platforms, big data, etc. I would love to connect with you on Linkedin.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.

Latest posts by Ajitesh Kumar (see all)

• Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
• LLMs for Adaptive Learning & Personalized Education - October 8, 2024
• Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024