Bayesian thinking is a powerful way of looking at the world, and it can be useful in many real-life situations. Bayesian thinking involves using prior knowledge to make more accurate predictions about future events or outcomes. It is based on the Bayes theorem, which states that the probability of an event occurring is determined by its prior probability combined with new information as it becomes available. It is important for data scientists to learn about Bayesian thinking because it can help them make accurate predictions and draw more meaningful insights from data. In this blog post, we will discuss Bayesian thinking and provide some examples from everyday life to illustrate how Bayesian reasoning can help us make better decisions.
What is Bayesian Thinking and How Does it Work?
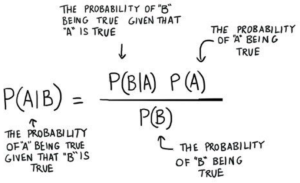
Bayesian thinking is a form of reasoning that utilizes Bayes’ theorem and prior knowledge to update beliefs based on data and experience. Bayesian thinking involves using this principle to update our beliefs in light of available data or observation, taking into account both our prior beliefs and any new information that has become available. This can be represented as the following:
- P(observed | belief): Probability of observing the data given the belief or hypothesis is true. Different observations could result in different belief and hence P(observed | belief) will continue to change.
- P(belief | observed): Probability that the belief or hypothesis holds good given the observation or data. This helps strengthening our belief about something based on the given data.
Let’s understand this with an example. Let’s say that the data observed is D, the belief or hypothesis is H1 and the prior experience is X related to data. The probability of the data D given the belief H1 and X is
[latex]P(D | H_{1}, X)[/latex]
The above can be read as the following: “The probability of the data given my hypotheses and experience in the world,” or in simpler words, “How well my beliefs explain what I observe”.
At a later time, you got some more data which resulted in different beliefs or hypotheses H2. The probability can be defined as the following given H2 and X
[latex]P(D_{updated} | H_{2}, X)[/latex]
From above, you can understand that the new data [latex]D_{updated}[/latex] results in updating of our belief H2.
In our day-to-day thinking, we also tend to think about how well our belief or hypothesis (H) is supported by the observed data (D) and my prior experience (X). This can be expressed by the following:
P(H | D, X)
In the case of P(D | H, X), the idea is to change beliefs based on prior experience (X) and observations made about the world. In the case of P(H | D, X), the data is gathered to support the existing beliefs or hypotheses (H). Bayesian thinking is about changing beliefs and updating the understanding of the real-life or real world. The data observed is real, so the beliefs or hypotheses need to shift to align with the data.
P(D | H) can be found as a function of P(H | D) based on Bayes formula which goes like the following:
[latex]P(D | H) = \frac{P(H | D) * P(D)}{P(H)}[/latex]
In terms of observations and belief, Bayes theorem can be written as the following:
[latex]P(data | belief) = \frac{P(belief | data)*P(data)}{P(belief)}[/latex]
We can reverse the above formula and find out how strong is our belief given the observation based on the following formula:
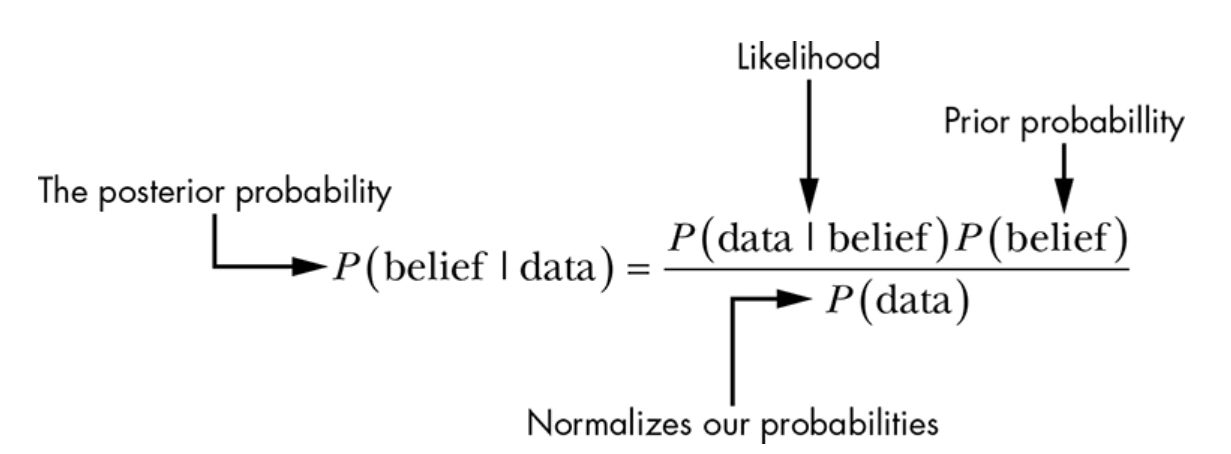
The Bayesian approach helps us make more accurate predictions about future events or outcomes based on our past experiences and data. By utilizing Bayes’ theorem, we can form updated beliefs (explanations for the occurrence of the data) that are better suited to current conditions than those held before. Thus, data should be used to update the belief and not the other way around. The new belief or hypothesis gets established by considering all of the available evidence when assessing a situation and factoring in both existing knowledge and new evidence as it becomes available. This enables us to form more accurate predictions while also accounting for potential unknowns and risks.
When applying Bayesian reasoning, one must consider all possible data or observations when making decisions or predictions. This means that all of the possibilities (data) must be taken into account when forming an opinion or making a prediction about a certain outcome or event. Bayesian reasoning encourages us to keep an open mind so that we can accurately assess a situation in light of all the relevant facts, not just those which may appear to support our preconceptions.
Real-life examples of Bayesian thinking
Bayesian thinking can be applied to real-life scenarios, from decisions related to business, health, finance, and more.
Bayesian thinking can be useful in decision-making because it allows us to incorporate prior knowledge, past experience, and available data into our decisions. A Bayesian approach uses the Bayes theorem formula to calculate the probability of an event based on prior beliefs and available data.
For example, let’s say you are trying to decide whether or not to invest in a certain stock. Using a Bayesian approach, you could take into account your prior knowledge of the market, as well as any research you have done to come up with a better-informed decision. You could also use the Bayes theorem formula to calculate the probability of success for that particular stock given your current situation. This way, you can make more informed decisions about where to allocate your resources and how much risk you’re willing to take.
Let’s take another example of understanding Bayesian thinking. let’s say a patient presents with fever, fatigue, and swollen lymph nodes. A doctor may suspect that the patient has lymphoma but wants to be sure before they recommend further treatments such as biopsies or chemotherapy. By using a Bayesian approach, the doctor can take into account their prior knowledge of similar cases and any research they have done on this particular disease, as well as any other available information about the patient (age, medical history, etc). The doctor can assess the probability of this particular illness and make an informed decision about whether or not further tests are necessary. Based on the feedback of the patients, doctors also update their belief about the cure of a disease. Let’s understand this with a formula.
When the patient first came, he/she told about the symptom, D. Based on the prior experience, X, the doctor arrived at hypothesis H that the person is suffering from lymphoma. This can be represented as the following:
P(D | H, X)
After two weeks, the patient gave feedback that his/her condition has improved after taking the medication. This information can be represented as [latex]D_{updated}[/latex]. This would strengthen the doctor’s hypothesis or belief. The following will be the representation:
[latex]P(D_{updated}|H, X)[/latex]
If the patient would have given different feedback such as his/her condition has worsened, the doctor’s hypothesis or belief would have changed to H1. The following will be the representation:
[latex]P(D_{updated}|H_1, X)[/latex]
Conclusion
Bayesian thinking is a great tool to have in your arsenal as it can help you make better decisions with the information that you have. Bayesian thinking should be used to update the belief based on the new data observed and prior experience and not the other way around. By understanding how it works and using some simple real-life examples, we can start to apply it to our own lives and improve the quality of our decision-making. If you would like to learn more about how Bayesian Thinking works or want to see some real-life examples of it in action, please drop me a message and I will be happy to chat with you further.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me