Have you ever wondered how machines can make decisions with uncertainty? What if there was an approach in machine learning that not only learned from data but also quantified and managed uncertainty in a principled way? Enter the realm of Bayesian machine learning.
Bayesian machine learning is one of the most powerful modeling technique in predictive analytics. It marries the probabilistic reasoning with machine learning algorithms. Bayes’ theorem, which was first introduced by Reverend Thomas Bayes in 1763, provides a way to infer probabilities from observations. Bayesian machine learning has become increasingly popular because it can be used for real-world applications such as spam filtering (NLP), credit card fraud detection, etc. In this blog post, we will discuss briefly about what is Bayesian machine learning and then get into the details of Bayesian machine learning real-world examples to help you understand how Bayes’ theorem works.
What is Bayesian Machine Learning?
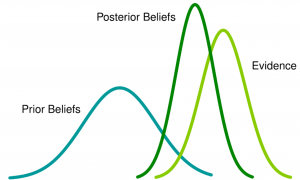
Bayesian Machine Learning is an approach that combines Bayesian statistics and machine learning to make predictions and inferences while explicitly accounting for uncertainty. It leverages Bayes’ theorem to update prior beliefs or probabilities based on observed data, enabling the estimation of posterior probabilities and making more informed decisions. Bayesian inference is grounded in Bayes’ theorem, which allows for accurate prediction when applied to real-world applications.
The fundamental formula behind Bayesian Machine Learning is Bayes’ theorem:
P(H|D) = (P(D|H) * P(H)) / P(D)
Where:
- P(H|D) is the posterior probability of hypothesis H given the observed data D.
- P(D|H) is the likelihood of the data D given the hypothesis H.
- P(H) is the prior probability of hypothesis H.
- P(D) is the probability of the observed data D.
In Bayesian Machine Learning, this formula is used to update prior beliefs (P(H)) based on new evidence (P(D|H)) and calculate the posterior probabilities (P(H|D)). The following is an example of spam filtering to illustrate Bayesian Machine Learning in action:
Let’s say we have a classification problem of distinguishing (filtering) between spam and non-spam emails. We start with prior beliefs about the probability of an email being spam, which is represented as P(spam) and P(non-spam). Based on a labeled dataset, we can calculate the likelihood of observing certain words or features in spam emails (P(Word|spam)) and non-spam emails (P(Word|non-spam)).
Now, given a new email with certain words, we want to determine whether it is spam or non-spam. Using Bayes’ theorem, we can update our prior beliefs to calculate the posterior probabilities:
P(spam|Word) = (P(Word|spam) * P(spam)) / P(Word)
P(non-spam|Word) = (P(Word|non-spam) * P(non-spam)) / P(Word)
By comparing these posterior probabilities, we can classify the email as spam or non-spam based on which probability is higher.
Bayesian Machine Learning Applications
Here are some great examples of real-world applications of Bayesian inference:
- Credit card fraud detection: Bayesian inference can identify patterns or clues for credit card fraud by analyzing the data and inferring probabilities with Bayes’ theorem. Credit card fraud detection may have false positives due to incomplete information. After an unusual activity is reported to enterprise risk management, Bayesian neural network techniques are used on the customer profile dataset that includes each customer’s financial transactions over time. These analyses confirm whether there are any indications of fraudulent activities.
- Spam filtering: Bayesian inference allows for the identification of spam messages by using Bayes’ theorem to construct a model that can tell if an email is likely to be spam or not. The Bayesian model trained using the Bayesian algorithm will take each word in the message into account and give it different weights based on how often they appear in both spam and non-spam messages. Bayesian neural networks are also used to classify spam emails by looking at the probability of an email being spam or not based on features like number of words, word length, presence/absence of particular characters etc.
- Medical diagnosis: Bayes’ theorem is applied in medical diagnoses to use data from previous cases and determine the probability of a patient having a certain disease. Bayesian inference allows for better prediction than traditional statistic methods because it can take into account all the factors that may affect an outcome and provide probabilities instead of just binary results. Bayes’ theorem is used to compute posterior probabilities, which are combined with clinical knowledge about diseases and symptoms to estimate the likelihood of a condition. Bayesian inference is used in the diagnosis of Alzheimer’s disease by analyzing past patient data and finding a pattern that can indicate whether a person has this condition. Bayes’ theorem is especially useful for rare diseases that may occur infrequently and require a large amount of data to make accurate predictions.
- Patterns in customer dataset/marketing campaign performance: Bayesian nonparametric clustering technique is used to find hidden patterns in data. Bayesian nonparametric clustering technique (BNC) is a powerful method that can be applied to various datasets such as customer datasets or marketing campaign performance. It helps find hidden patterns in data because Bayesian machine learning does not require any assumptions about the distribution of input variables. BNC enables you to find clusters that are statistically significant and can be generalized across other datasets as well.
- Help robots make decisions: Bayesian inference is used in robotics to help robots make decisions. Bayes’ theorem can be applied by using real-time sensor information from the robot’s environment and inferring about its next move or action based on previous experiences. Robots will use Bayes’ theorem for extracting relevant features such as speed, the direction of movement, obstacles, and other objects in the environment. Bayesian reinforcement learning can be applied to robot learning. Bayesian reinforcement learning (BRL) uses Bayes’ theorem to compute the probability of taking a certain action based on previously learned experiences/knowledge and observations received from sensory information. BRL has been shown to outperform other machine learning algorithms such as deep Q-learning, Monte Carlo Tree Search, and Temporal Difference Learning.
- Reconstructing clean images from noisy images: Bayes’ theorem is used in Bayesian inverse problems such as Bayesian tomography. Bayesian inference can be applied to the problem of reconstructing images from noisy versions of those images using Bayes’ theorem and Markov Chain Monte Carlo (MCMC) algorithms.
- Weather prediction: Bayesian inference can be used in Bayesian machine learning to predict the weather with more accuracy. Bayes’ theorem can be applied for predicting real-time weather patterns and probabilities of rain based on past data such as temperature, humidity, etc. Bayesian models compare favorably against classical approaches because they take into account the historical behavior of the system being modeled and provide a probability distribution over the possible outcomes of the forecast.
- Speech emotion recognition: Nonparametric hierarchical neural network (NHNN), a lightweight hierarchical neural network model based on Bayesian nonparametric clustering (BNC), can be used to recognize emotions in speech with better accuracy. NHNN models generally outperform the models with similar levels of complexity and state-of-the-art models in within-corpus and cross-corpus tests. Through clustering analysis, is is shown that the NHNN models are able to learn group-specific features and bridge the performance gap between groups.
- Estimating gas emissions: The recent findings suggest that a large fraction of anthropogenic methane emissions is represented by abnormal operating conditions of oil and gas equipments. As such, effective mitigation requires rapid identification as well as repairs for faulty sources controlled via advanced sensing technology or automatic fault detection algorithms based on recursive Bayes’ techniques.
- Federated analytics (Faulty device detection, malfunctions) : Bayesian approach can be applied to federated analytics, a new approach to data analytics involving an integrated pipeline of machine learning techniques. The Bayesian hierarchical model allows the user to interrogate the aggregated model and automatically detect anomalies that could indicate faulty devices, malfunctions, or other such problems with remote assets/sensor networks. Federated learning is the methodology that provides a means of decentralized computations for machine learning without a need for moving local data of users. In each round of the federated learning, the participating devices train a model on their respective local data and send only an encrypted update to the aggregator. The aggregator combines updates from all participants to improve a shared model followed by its distribution to all participants.
- Forensic analysis: Bayesian inference can be used in Bayesian machine learning to infer the identity of an individual based on DNA evidence. Bayes’ theorem is applied for forensic analysis, which involves reasoning about conditional probabilities and making statistical inferences from observed data (genetic marker alleles) with respect to one or more populations of possible genotypes under study.
- Optical character recognition (OCR): Bayesian inference can be used in Bayesian machine learning to improve optical character recognition (OCR) performance. Bayes’ theorem is applied for OCR, which involves the transformation of images captured on paper-based media into text strings that are computer-readable. Bayesian approaches have been shown to provide more accurate results compared with conventional machine learning algorithms.
Bayesian machine learning is a subset of Bayesian statistics that makes use of Bayes’ theorem to draw inferences from data. Bayesian inference can be used in Bayesian machine learning to predict the weather with more accuracy, recognize emotions in speech, estimate gas emissions, and much more! If you’re interested in learning more about how Bayes’ theorem could help, let us know.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com
- Mean Squared Error vs Cross Entropy Loss Function - April 28, 2024
- Cross Entropy Loss Explained with Python Examples - April 28, 2024
- Logistic Regression in Machine Learning: Python Example - April 26, 2024
Leave a Reply