Machine Learning – How to Debug Learning Algorithm for Regression Model

This article represents some of the key reasons for larger prediction error while working with regression models and, what one could do to solve the prediction error. Below mentioned techniques could be used for both, linear and logistic regression models. As a matter of fact, below arguments could also be used to debug an artificial neural network. In place of features, what is considered is number of hidden layers and units. Please feel free to comment/suggest if I missed to mention one or more important points. Also, sorry for the typos.

• Key Reasons for Larger Prediction Error
• Key Techniques to Reduce the Prediction Error

Key Reasons for Larger Prediction Error

When working with machine learning algorithm, the primary objective is to minimize the error between predicted and observed value by minimizing the cost function  which, for regression models, is mean squared difference between predicted and observed value (added with regularization if required). Below argument can as well be applied for neural network. Following are different reasons why large prediction errors could be found while working with linear or logistic regression models.

• Lack of enough features: At times, due to inclusion of less number of features as part of machine learning algorithm, one can often get caught with the case of high bias or under-fitting. And, this might not get better after a point however one tries with adding additional training examples. In case of neural network, the analogy is the lack of enough number of hidden units.
• Inclusion of lot of features: At times, inclusion of lot of features results in high variance or over-fitting. That would lead to lesser error with training set but greater error with cross-validation or test data set. That may require a very large data set for the training data set error and cross-validation error to merge. In case of neural network, the analogy is the the scenario in which neural network has large number of hidden units.
• Inappropriate regularization parameter: In many cases, the choice of regularization parameter may as well result in high bias or high variance case.

Key Techniques to Reduce the Prediction Error

Following are some of the techniques that one could use to reduce the prediction error and further optimize the regression models. Note that the error results from common reasons such as high bias (under-fitting) or high variance (over-fitting)

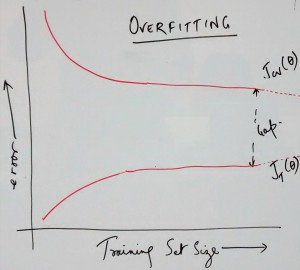
• Collect lots of data or training examples: The absence of sufficient number of training examples is one of the common reasons why one could get larger prediction error with cross-validation or test data set. The primary reason is that the learning algorithm would try and fit the data very well resulting in very less training error but large cross-validation or test error. In simpler words, the models could not be generalized. This could be solved by increasing the size of training data sets which results in reduction of cross-validation or test data set error. In case of over-fitting problem, adding large number data set leads to reduction of error. Thus, this could be used to fix error due to the high variance or over-fitting problem because adding further training examples would result in convergence of training and cross-validation/test error. Pay attention to the diagram below that represents the convergence of training and cross-validation data set error as dotted line. That said, that would, however, fail to reduce the error with the data set having high bias or under-fitting problem. Following diagram represents the reduction of error with cross-validation set for the case of over-fitting and under-fitting.
  

  Over-fitting Error vs Training Set Size

• Try with smaller set of features: At times, inclusion of large number of feature set results in over-fitting or high variance for training data set. That would lead to larger error when working with cross-validation or test data set and hence, the model could not be generalized. This technique would fix error occurring due to over-fitting or high variance problem. The way to solve this problem is to do some of the following:
  • Reduce the number of features and include only the most important features. However, this must be done with utmost care and suggestion from domain expert may be seeked to achieve the best result.
  • Introduce the regularization parameter. This is explained later in this article.
• Try adding more features: Because of the fact that inclusion of less number or inappropriate features lead to high bias, this could lead to the prediction error. This could be solved by inclusion of appropriate number or larger set of features. However, the care should be taken to avoid the over-fitting problem. Tus, adding more features may fix the error occurring due to high bias or under-fitting.
• Try adding polynomial features: This would lead to inclusion of further features and hence fix the error occurring due to high bias or under-fitting.
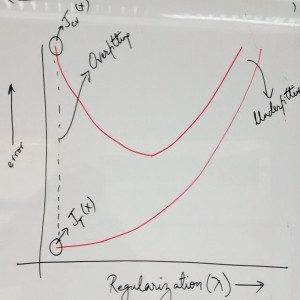
• Try decreasing regularization parameter: This would result in reduction of error that might have occurred due to high bias or under-fitting. Note that high value of regularization parameter would mean value low value of parameters (refer cost function with regularization parameter) and hence high bias or under-fitting problem. However, care must be taken to make sure that regularization parameter have not been reduced to such a low value that would lead to high cross-validation or test set error. In the following diagram, pay attention to how decreasing the regularization parameter after an extent leads to increase in cross-validation error due to which the model could not be generalized.
  

  Error vs Regularization Parameter

• Try increasing regularization parameter: This would result in reduction of error that might have occurred due to over-fitting or high variance problem. Again, the care must be taken to increase to an optimum level which results in optimum error of cross-validation or test data set. Check the above diagram which represents the fact that increasing regularization parameter after an extent leads to increase in cross-validation error and hence, the model could not be generalized.