Tensors are a hot topic in the world of data science and machine learning. But what are tensors, and why are they so important? In this post, we will explain the concepts of Tensor using Python Numpy examples with the help of simple explanation. We will also discuss some of the ways that tensors can be used in data science and machine learning. When starting to learn deep learning, you must get a good understanding of the data structure namely tensor as it is used widely as the basic data structure in frameworks such as tensorflow, PyTorch, Keras etc. Stay tuned for more information on tensors!
What are tensors, and why are they so important?
Tensors are a key data structure in many machine learning and deep learning algorithms. Tensors are mathematical objects that generalize matrices to higher dimensions. Just as matrices are used to represent linear transformations, tensors can be used to represent more general types of transformations. Tensors are also the natural data structure for representing multidimensional data, such as images, video, and other types of data. The power of tensors comes from the fact that they can be used to efficiently represent very high-dimensional data. For example, a tensor with 10^6 elements can represent a million-dimensional vector. Tensors are thus an essential tool for handling large-scale datasets. In addition, tensors can be easily manipulated using the powerful tools of linear algebra. This makes them well suited for use in deep learning algorithms, which often require the efficient manipulation of large amounts of data.
Simply speaking, Tensor is a container of data. The data can be numerical or character. However, mostly, tensors hold numbers or numerical data. Tensors can be represented as an array data structure. In this post, you will learn about how to express tensor as 1D, 2D, 3D Numpy array. Before going ahead and see the examples of 1D, 2D and 3D tensors, lets understand the key features of tensors:
- Rank or Number of Axes: Number of axes of a tensor is also termed as the rank of the tensor. Simply speaking, the axes or rank of the tensor represented as an array is number of indices that will be required to access a specific value in the multi-dimensional array aka tensor. Accessing a specific element in a tensor is also called as tensor slicing. The first axis of the tensor is also called as a sample axis.
- Shape: Tuple of integers representing the dimensions that the tensor have along each axes.
Tensors can be used to represent data in a variety of ways, including as a sequence, as a graph, or as a set of points in space. In data science and machine learning, tensors are often used to represent high-dimensional data. Tensors can also be used to represent complex relationships between variables. For example, in machine learning, tensors can be used to represent the weights of a neural network.
What are the different types of tensors?
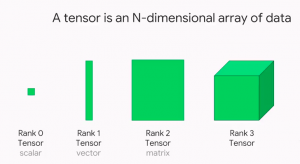
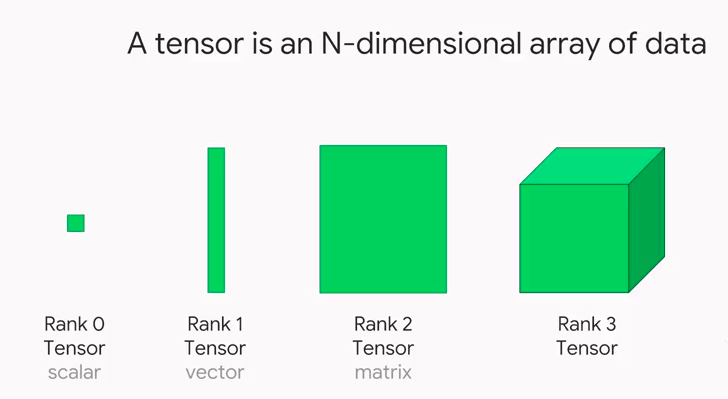
As learned in the previous section, tensors are mathematical objects that generalize scalars, vectors, and matrices. In other words, they are a natural extension of the concept of vectors and matrices to higher dimensions. Tensors come in different forms, depending on their dimensionality. A 0D tensor is simply a scalar value, while a 1D tensor is a vector. A 2D tensor is a matrix, and a 3D tensor is an array of matrices. Tensors of higher dimensions are simply called N-dimensional tensors or N-tensors. Tensors are used extensively in deep learning and data science.
Lets look at the diagram given below which represents 0D, 1D, 2D and 3D tensors. 0D tensor is a scalar data or simply a number.
Tensors are used in many different areas of deep learning, such as image recognition and natural language processing. One type of tensor is the weight tensor. Weight tensors are used to store the weights of the connections between neurons in a neural network. The weights are usually initialized randomly before training begins. Another type of tensor is the input tensor. Input tensors contain the input data for a neural network. This data can be anything from images to text data. The input tensor must have the same number of dimensions as the weight tensor. Another type of tensor is the output tensor. Output tensors contain the results of the forward propagation through a neural network. The output tensor will have the same number of dimensions as the input tensor.
1D Tensor (Vector) Example
A one-dimensional array also called as vector can be termed as a 1D-tensor. 1D tensor represents the tensor of rank/axes as 1. Take an example of an array representing the tensor using the following 1D Numpy array:
#
# Tensor having rank / axes = 1 and dimension along the axis as 3
#
x = np.array([56, 183, 1])
#
# Dimension = 1
# Shape = 1,
#
x.ndim, x.shape
In the above example, the axes or rank of the tensor x is 1. The axes of the tensor can be printed using ndim command invoked on Numpy array. In order to access elements such as 56, 183 and 1, all one needs to do is use x[0], x[1], x[2] respectively. Note that just one indices is used. Printing x.ndim, x.shape will print the following: (1, (3,)). This represents the fact that the tensor x has the axes or rank has 1 and there are three dimension on that axes.
2D Tensor (Matrix) Example
A two-dimensional array also called as matrix can be termed as a 2D-tensor. 2D tensor represents the 2-dimensional array which is nothing but a matrix. As like matrices, the two-dimensional array can be represented as a set of rows and columns. Here is the code for 2D numpy array representing 2D tensor:
#
# Tensor having rank / axes = 2 and dimension along each axis as 3
#
x = np.array([[56, 183, 1],
[78, 178, 2],
[50, 165, 0]])
#
# Dimension = 2
# Shape = 3, 3
#
x.ndim, x.shape
Printing x.ndim, x.shape will print the following: (2, (3,3)). This represents the fact that the tensor x has the axes or rank has 2 and there are three dimension on each of the axes. n order to access elements such as 56, 178 and 50, one would require to use the following respectively: x[0][0], x[1][1], x[2][0]. Note that you will need two indices to access a particular number.
3D Tensor Example
A three-dimensional array can be termed as a 3D-Tensor. Here is the code representing the 3D tensor:
#
# Tensor having rank / axes = 3 and dimension along the axis as 3
#
x = np.array([[[56, 183, 1],
[65, 164, 0]],
[[85, 176, 1],
[44, 164, 0]]])
#
# Dimension = 3
# Shape = (2, 2, 3),
#
x.ndim, x.shape
Printing x.ndim, x.shape will print the following: (3, (2, 2, 3)). This represents the fact that the tensor x has the axes or rank has 3. In order to access elements such as 56, 176 and 44, one would require to use the following respectively: x[0][0][0], x[1][0][1], x[1][1][0]. Note that you will need three indices to access a particular number and hence, the rank of the tensor is 3.
Understanding Tensor using MNIST Image Example
Here is an explanation of tensor axes / rank and shape using Keras and MNIST dataset.
from keras.dataset import mnist
#
# Load the training and test images MNIST Dataset
#
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
#
# Accessing the tensor rank / axes and shape
#
print(train_images.ndim, train_images.shape)
Executing the above would print the information about the tensor rank / axes and the shape – 3 (60000, 28, 28). It represents the fact that training images is stored in a 3D tensor of axes 3 and having shape representing 60,000 matrices of 28×28 integers.
Conclusions
Here is what you learned about tensors with the help of simple Python Numpy code samples.
- Tensor can be defined as a data container. It can be thought of as a multi-dimensional array.
- Numpy np.array can be used to create tensor of different dimensions such as 1D, 2D, 3D etc.
- A vector is a 1D tensor, a matrix is a 2D tensor. 0D tensor is a scalar or a numerical value.
- Accessing a specific value of tensor is also called as tensor slicing.
- Two key attributes of tensors include A. rank or axes of tensor B. Shape of the tensor
- ndim and shape when invoked on Numpy array gives the axes / rank and shape of the tensor respectively.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
hi. thank you. description for 3D Tensor Example is not correct. it is the repeated text of above example.
Thank you for pointing that out. Corrected it.
Thank you
Just wanted to clarify. The last example’s comments say that the shape is 3,3,2. Isn’t it 2,2,3 or I don’t understand something right?
Thanks for pointing it out correctly. Made the changes.