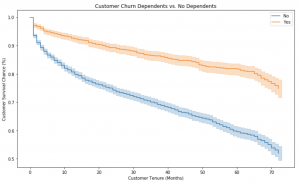
Customer churn is a prevalent problem for many businesses. It can happen in several different ways, such as when customers stop using the product, or when they leave because of an issue with customer service. This blog post will explore survival analysis modeling and what it can do to help you better understand customer churn problems. First, we will discuss survival analysis itself and why it is beneficial for analyzing customer behavior. Then we will show some examples on how survival analysis has been used to analyze customer churn problems. As data scientists, it will be good to familiarize ourselves with survival analysis, as it is a popular modeling technique that can be used in many different scenarios.
What is customer churn problem?
Customer churn problem is a problem of survival analysis. It is a business decision-making process to describe customer behavior during the time period before they stop doing business with us, and decide to move on to another supplier or not purchase anymore from any provider at all.
Customer churn can be defined as every case where a customer decides that she/he wants to end the relationship with a company. There are several factors that can increase customer churn, such as poor service quality or pricing. Customer churn not only means that the customer is moving to another company, but it can also mean losing a customer in terms of reducing purchases or being late with payments.
There are several ways to decrease customer churn rate and increase survival analysis for customers who decide to stay loyal despite all challenges our business might face during their period working together. Customer retention strategies include running marketing campaigns to reach out the customers. These campaigns might be about discounts or special offers, or it can also involve customer education for better understanding of product features and benefits. This technique is often used by organizations that are engaged in subscription-based business models – for example phone companies offer unlimited calling plans to their clients during the first few months or years of their service.
What is survival analysis?
Survival analysis is defined as the survival of an object or the length of time until some event occurs. This type of statistical analysis is used to analyze data collected on individuals, such as how long it takes before they die. Survival models are very flexible because they allow researchers to use any type of survival data that they collect. This type of statistical analysis can be used to analyze how long it takes for something to happen before the event occurs or is completed. Survival analysis can be applied to customer churn rates and credit risk models which examine factors that affect repayment timelines for loans.
Customer churn survival analysis is commonly implemented using statistical methods like survival, hazard and event history models (Aalen Additive Hazards model). We can also use machine learning algorithms to increase the accuracy of customer retention strategies by applying techniques such as pattern recognition for identifying customers at risk with high probability.
Apart from customer churn, survival analysis can also be applied to analyzing other types of survival data. For example, the length of time that it takes for a machine to produce its first failure can also be analyzed. This type of analysis is used in quality control and reliability engineering where engineers try to predict how long something will last or function before breaking down.
What are different types of customer churn survival analysis?
Survival models can analyze any type of survival data that researchers want to study, but most commonly this type of statistical model focuses on time-to-event or survival data. There are several different types of survival analysis, each of which is used to examine different types of events. The following represents some of the types of survival analysis models that can be used for customer churn:
- Aalen additive hazard survival models are used to study the cumulative incidence function, which is defined as the probability that an event occurs within a specific duration of follow-up or observation period. This type of survival analysis can be applied to customer churn data where survival refers to how long it takes for customers to cancel their subscriptions. This type of survival analysis can be applied when you want to study customers who have not yet canceled their service plans and look at factors that may be causing them to do so. Some other real-life examples where Aalen additive hazard models got used include survival of human patients and survival analysis for medical research and survival rates in financial time series.
- Event history survival models are survival models that are applied to survival data collected for more than one time period. This type of survival analysis can be used when event history data is collected over several different periods of time. Event history survival analysis is often confused with the term survival curves, but these are actually two different types of survival analyses. An example would be if you want to study customers who have canceled their service plans while they were still in the trial period. You would then use an Aalen additive hazards model on event history survival data, which can analyze how many customers canceled their subscription at various times during the trial period.
- Markov survival models are survival models that can be used to study the timing between events. Markov survival models are time-independent, which means they only consider the event history without considering any other previous information. This type of survival analysis is often applied in cohort studies where researchers do not have access to all of the customer data or may need to remove any customer data that may not be relevant to survival analysis. An example would be if you want to study the number of customers who canceled their service plan, but only those who cancelled during a specific time period. The Markov survival model can then help determine how many customers or subscribers have been lost and at what point they left your subscription services.
- The log rank test survival models are another type of survival analysis that is often used to compare and study survival rates between groups. This type of survival analysis is often applied in cohort studies where researchers only have survival data and do not know or cannot access any other customer information, such as subscription service plans. The log rank test survival models can then determine if there are significant differences between the survival rates of different groups during a certain time period.
- Cox Proportional Hazards models are used when survival data is collected in larger number of time points. This type of survival analysis can be applied if you want to study how different factors affect the survival rate at certain periods in time. These survival models assume that there’s a baseline survival curve and modifies it with another survival curve based on your observations. For example, you could use this for analyzing customer churn and see how different factors affect customers who have already canceled their subscriptions during a specific period in time.
How to use survival analysis for customer churn problems?
The following represent the common steps for using survival analysis for customer churn problem:
- First and foremost, you need to identify the survival time or survival event that you want to study. For example, if we are interested in how long it takes for a customer to cancel their service (survival event), then we would consider “time-to” cancellation as survival data points and use them for studying this type of problem.
- Second, identify the data you have or would like to collect and make sure it is sufficient in order to answer your survival question. For example, if you are interested in survival time of customers between two periods (e.g., March 2018 – Nov 2018), then you will want to have survival data for the time period of March 2018 – Nov 2018.
- Third, decide what type of survival analysis you want to use. The following list includes some common types: hazard models, censored survival models and event history models.
- Fourth, determine the survival function that will be used (e.g., exponential, Weibull or Gompertz) based on what type of survival analysis was chosen in step three above. This survival function will help identify the shape of your survival curve and how it relates to other survival curves (e.g., exponential, Weibull or Gompertz). For example, if you chose a hazard models, then you will want to use survival models such as Weibull, exponential or Gompertz.
- Fifth, choose an appropriate model for your problem and use it to make predictions about future events when you have new data added – such as customer characteristics. You can also compare these results with actual survival times that occurred in the past (e.g., survival time). This will allow you to determine whether or not your predictions are accurate and if they should be used in future analyses.
- Lastly, validate the survival model’s results by comparing them to actual events that have occurred – such as survival time. This will allow you to determine whether or not your predictions are accurate and if they should be used in future analyses.
This survival analysis post has covered survival modeling for customer churn, which is a common problem in the world of business. You’ve learned about different types of survival models and how to use them based on your needs. For example, if you want to know when customers are most likely to cancel their service (survival event) then you will want to study hazard models or Weibull survival analysis. If you would like information related to censored survival data points that have an end time limit (e.g., people who live 100 years old), then censoring survival analysis may be best suited for this type of question. Regardless of what type of model you need, it helps first identify the appropriate one so as not waste valuable resources on something that will not provide you with the necessary survival analysis results. Finally, survival models can be used to make predictions about future events and compare them to actual survival times that occurred in the past (e.g., survival time) which will allow you to determine if your predictions are accurate or should be used for future analyses – such as customer characteristics. If you would like to know further, please drop a message.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me