In this post, you will learn about one of feature selection techniques namely sequential forward selection with Python code example. Refer to my earlier post on sequential backward selection technique for feature selection. Sequential forward selection algorithm is a part of sequential feature selection algorithms. Some of the following topics will be covered in this post:
- Introduction to sequential feature selection algorithms
- Sequential forward selection algorithm
- Python example using sequential forward selection
Introduction to Sequential Feature Selection
Sequential feature selection algorithms including sequential forward selection algorithm belongs to the family of greedy search algorithms which are used to reduce an initial d-dimensional feature space to a k-dimensional feature subspace where k < d. The idea is to select a subset of features that is most relevant to the problem, which results in optimal computation efficiency while achieving reduced generalization error by filtering out irrelevant features (that acts as a noise).
Some of the common techniques used for feature selection includes regularization techniques (L1 / L2 norm) and sequential forward / backward feature selection. For those algorithms such as K-Nearest Neighbours which do not support regularisation techniques, sequential feature selection is commonly used. Here is a good read on sequential feature selection technique. Note that the sequential feature selection techniques are based on greedy search algorithms which applies combinatorial methods for feature search.
Sequential Forward Selection & Python Code
Sequential forward selection algorithm is about execution of the following steps to search the most appropriate features out of N features to fit in K-features subset.
- First and foremost, the best single feature is selected (i.e.,using some criterion function) out of all the features.
- Then, pairs of features are formed using one of the remaining features and this best feature, and the best pair is selected.
- Next, triplets of features are formed using one of the remaining features and these two best features, and the best triplet is selected.
- This procedure continues until a predefined number of features (K features) are selected.
Here is the Python code sample for the algorithm. Note some of the following in the code:
- Code block for finding the first / single feature having best score
- Code block for adding the features one by one until k_features is reached
- Fit method to find the most appropriate indices in the feature list representing the best features
- Transform method to output the best features
- Attributes such as indices_, subsets_, scores_ etc to find the best subsets and related best scores
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from itertools import combinations
from sklearn.base import clone
from sklearn.metrics import accuracy_score
class SequentialForwardSelection():
'''
Instantiate with Estimator and given number of features
'''
def __init__(self, estimator, k_features):
self.estimator = clone(estimator)
self.k_features = k_features
'''
X_train - Training data Pandas dataframe
X_test - Test data Pandas dataframe
y_train - Training label Pandas dataframe
y_test - Test data Pandas dataframe
'''
def fit(self, X_train, X_test, y_train, y_test):
max_indices = tuple(range(X_train.shape[1]))
total_features_count = len(max_indices)
self.subsets_ = []
self.scores_ = []
self.indices_ = []
'''
Iterate through the feature space to find the first feature
which gives the maximum model performance
'''
scores = []
subsets = []
for p in combinations(max_indices, r=1):
score = self._calc_score(X_train.values, X_test.values, y_train.values, y_test.values, p)
scores.append(score)
subsets.append(p)
#
# Find the single feature having best score
#
best_score_index = np.argmax(scores)
self.scores_.append(scores[best_score_index])
self.indices_ = list(subsets[best_score_index])
self.subsets_.append(self.indices_)
#
# Add a feature one by one until k_features is reached
#
dim = 1
while dim < self.k_features:
scores = []
subsets = []
current_feature = dim
'''
Add the remaining features one-by-one from the remaining feature set
Calculate the score for every feature combinations
'''
idx = 0
while idx < total_features_count:
if idx not in self.indices_:
indices = list(self.indices_)
indices.append(idx)
score = self._calc_score(X_train.values, X_test.values, y_train.values, y_test.values,indices)
scores.append(score)
subsets.append(indices)
idx += 1
#
# Get the index of best score
#
best_score_index = np.argmax(scores)
#
# Record the best score
#
self.scores_.append(scores[best_score_index])
#
# Get the indices of features which gave best score
#
self.indices_ = list(subsets[best_score_index])
#
# Record the indices of features for best score
#
self.subsets_.append(self.indices_)
dim += 1
self.k_score_ = self.scores_[-1]
'''
Transform training, test data set to the data set
havng features which gave best score
'''
def transform(self, X):
return X.values[:, self.indices_]
'''
Train models with specific set of features
indices - indices of features
'''
def _calc_score(self, X_train, X_test, y_train, y_test, indices):
self.estimator.fit(X_train[:, indices], y_train.ravel())
y_pred = self.estimator.predict(X_test[:, indices])
score = accuracy_score(y_test, y_pred)
return score
Python example using sequential forward selection
Here is the code which represents how an instance of LogisticRegression can be passed with training and test data set and the best features are derived. Although regularization technique can be used with LogisticRegression, this is just used for illustration purpose.
#
# Instantiate the estimator - LogisticRegression
#
lr = LogisticRegression(C=1.0, random_state=1)
#
# Number of features
#
k_features = 5
#
# Instantiate SequentialBackwardSearch
#
sfs = SequentialForwardSelection(lr, k_features)
#
# Fit the data to determine the k_features which give the
# most optimal model performance
#
sfs.fit(X_train, X_test, y_train, y_test)
#
# Transform the training data set to dataset having k_features
# giving most optimal model performance
#
X_train_sfs = sfs.transform(X_train)
#
# Transform the test data set to dataset having k_features
#
X_test_sfs = sfs.transform(X_test)
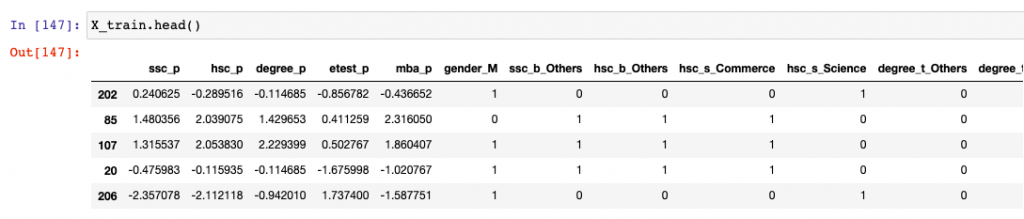
Here is a glimpse of the training data used in the above example:
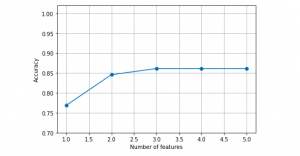
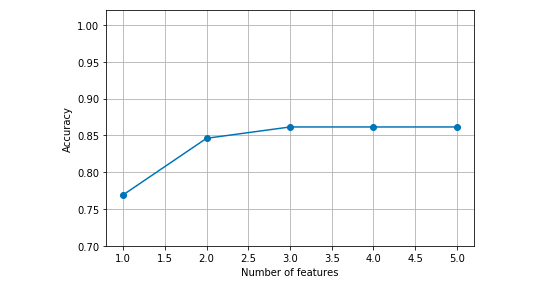
Here is the plot representing the model performance vs number of features which got derived from executing sequential forward selection algorithm.
k_features = [len(k) for k in sfs.subsets_]
plt.plot(k_features, sfs.scores_, marker='o')
plt.ylim([0.7, 1.02])
plt.ylabel('Accuracy')
plt.xlabel('Number of features')
plt.grid()
plt.tight_layout()
plt.show()
Here is how the plot would look like:
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me