In statistics, population and sample are two fundamental concepts that help us to better understand data. A population is a complete set of objects from which we can obtain data. A population can include all people, animals, plants, or things in a given area. On the other hand, a sample is a subset of the population that is used for observation and analysis. In this blog, we will further explore the concepts of population and samples and provide examples to illustrate the differences between them in statistics.
What is a population in statistics?
In statistics, population refers to the entire set of objects or individuals about which we want to draw conclusions. For example, if a researcher is studying drug usage in prison populations, the population would include all inmates who are serving time in prisons across the country. In general, a population can be divided into two categories: finite and infinite. A finite population consists of a limited number of objects that can be counted, whereas an infinite population is theoretically unlimited and cannot be counted completely.
The size of a population can vary from small groups to very large datasets. In order to make statistical inferences about such populations, researchers often rely on sampling techniques. This involves taking a sample (discussed in the next section) from the population and using it as an approximation for the entire group. The accuracy of any statistical inference relies heavily on sample size; larger samples tend to provide more accurate estimates than smaller ones do. Furthermore, it is important to ensure that samples are random and representative of the entire population in order to avoid bias and increase reliability.
Population statistics can be used in various fields including economics, public health and many others. They are also essential when it comes to calculating indicators like per capita income or life expectancy at birth; by accurately understanding the size and composition of different populations, governments can better allocate resources amongst their constituencies and develop policies that will benefit everyone involved.
What is a sample in statistics?
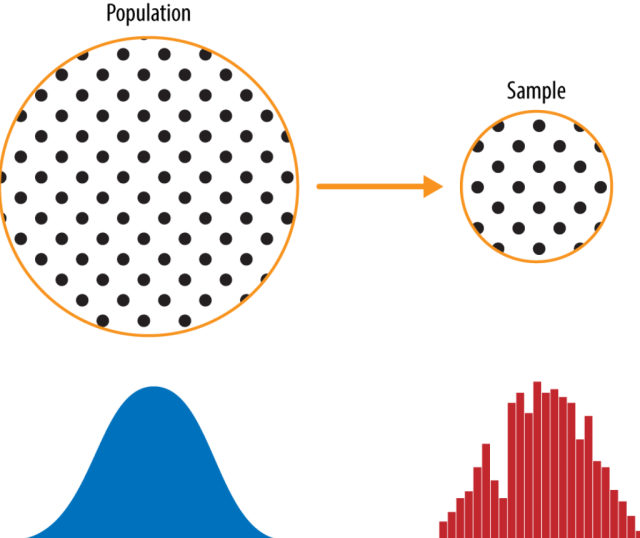
In statistics, the concept of a sample is extremely important and is used in many different forms of analysis. A sample can be thought of as a subset of a larger population that allows us to make conclusions about the overall population, based on just one smaller group. The following visually represents population and sample. Note the difference in probability distribution as well.
A sample must meet certain criteria in order for it to be considered valid for statistical analysis. Two key characteristics that a sample should possess are randomness and representativeness.
Sample randomness means that every individual unit within the population has an equal chance of being selected for the sample. This is often achieved by randomly selecting subjects from the population or using a random numbers table and ensuring that each participant is treated equally when entering into the study. Random sampling helps to eliminate any potential bias or skew in results caused by selection processes that may be inherently unequal in some way, such as gender or age.
A real-world example of a random sample and how one can go about creating a random sample is for a student survey. For instance, if a researcher wanted to collect information from college students about their study habits, they could create a random sample by randomly selecting participants from the student body. To do this, they could use a list of all enrolled students at the college and use a random number generator to select participants from the list. The researcher should ensure that the sample is truly random by choosing students without any bias or preconceived notion of what type of student will be selected in order to get an accurate picture of the entire student population.
Sample representativeness means that the subset of population chosen as sample accurately reflects the members of the entire population. In other words, sample representativeness describes how closely a sample mirrors the characteristics of the entire population. To be truly representative, each characteristic should correspond almost exactly with those of the wider population. This can be difficult to achieve depending on your selection method as you could end up with very few subjects which might not accurately reflect all aspects of the population at large; however, this can be beneficial if you are looking at specific details within a small group and want to draw conclusions from it rather than from an entire population set.
A real-world example of a representative sample would be a survey conducted by a market research firm to determine the average age of people who attend rock concerts. To create a representative sample, the market research firm would need to collect data from individuals who have attended at least one rock concert within the past five years. This could be done through an online survey sent out to a random sample of emails or through physical surveys distributed at various concert venues. The most important factor in creating a representative sample is making sure that the demographic makeup of the respondents reflects that of the overall population attending rock concerts. To achieve this, it is important for the firm to consider factors such as age, gender, income level, and geography when selecting participants. They should strive to ensure that there is an equal representation from all areas within their target market so that results are reflective of everyone’s experience in attending rock concerts.
In order for a sample to be valid for statistical analysis, it must also adhere to certain rules including size, variance, sample accuracy and independence between units within it. The larger the sample size, generally speaking, the more accurate your results will be – but too large samples can become unwieldy and difficult to manage! Variance describes how much difference there is between individual data points; higher amounts indicate greater differences between data points while lower amounts indicate similarity between them; this helps ensure that your data isn’t overly clustered or skewed towards one extreme or another which could lead to inaccurate inferences made from your findings. Sample accuracy explains whether or not your sampling technique is suitable for your intended use – meaning whether or not all elements from within the desired population have been given equal likelihoods of being chosen for inclusion in your study; Sample independence requires that no two individuals included in your study are linked in any way – thereby minimizing bias caused by relationships between participants which may influence their responses during research interviews or surveys conducted as part of your project.
Conclusion
In statistics, a population is defined as the entire set of objects or items from which samples can be drawn. A sample is just a smaller selection taken from the population. It’s important to note that when scientists talk about populations, they are usually talking about very large groups of things like all humans on Earth or every atom in the universe. The word “population” can also refer to animals, plants, and even inanimate objects like stars or galaxies. When taking data from any sort of population, it’s important to carefully consider whether you want to use information gathered from the entire group (a census) or just a portion of it (a sample). This decision can have major implications for your research results. If you’re not sure whether you should use data gathered from a population or a sample statistic in your next project, reach out and I’d be happy to help you figure it out.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me