K-Fold Cross Validation in Machine Learning – Python Example

Last updated: 3rd Jan, 2024

In this post, you will learn about K-fold Cross-Validation concepts used while training machine learning models with the help of Python code examples. K-fold cross-validation is a data splitting technique that can be implemented with k > 1 folds. K-Fold Cross Validation is also known as k-cross, k-fold cross-validation, k-fold CV, and k-folds. The k-fold cross-validation technique can be implemented easily using Python with scikit learn (Sklearn) package which provides an easy way to implement training of k-fold cross-validation models.  It is important to learn the concepts of k-fold cross-validation concepts in order to perform model tuning with the end goal to choose a model which has a high generalization performance. 

What and Why of K-fold Cross-Validation

K-fold cross-validation is defined as a method for estimating the performance of a model on unseen data. This technique is recommended to be used when the data is scarce and there is an ask to get a good estimate of training and generalization error thereby understanding the aspects such as underfitting and overfitting. This technique is used for hyperparameter tuning such that the model with the most optimal value of hyperparameters can be trained.  It is a resampling technique without replacement. The advantage of this approach is that each example is used for training and validation (as part of a test fold) exactly once. This yields a lower-variance estimate of the model performance than the holdout method. As mentioned earlier, this technique is used because it helps to avoid overfitting, which can occur when a model is trained using all of the data. By using k-fold cross-validation, we are able to “test” the model on k different data sets, which helps to ensure that the model is generalizable.

The following is done in this technique for training, validating, and testing the model:

1. The dataset is split into training and test dataset.
2. The training dataset is then split into K-folds.
3. Out of the K-folds, (K-1) fold is used for training
4. 1 fold is used for validation
5. The model with specific hyperparameters is trained with training data (K-1 folds) and validation data as 1 fold. The performance of the model is recorded.
6. The above steps (step 3, step 4, and step 5) is repeated until each of the k-fold got used for validation purpose. This is why it is called k-fold cross-validation.
7. Finally, the mean and standard deviation of the model performance is computed by taking all of the model scores calculated in step 5 for each of the K models.
8. Step 3 to Step 7 is repeated for different values of hyperparameters.
9. Finally, the hyperparameters which result in the most optimal mean and the standard deviation of model scores get selected.
10. The model is then trained using the entire training data set (step 2) and the model performance is computed on the test data set (step 1).

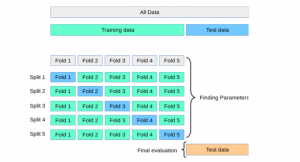
Here is the diagram representing steps 2 to steps 7. The diagram is taken from the book, Python Machine Learning by Dr. Sebastian Raschka and Vahid Mirjalili. The diagram summarises the concept behind K-fold cross-validation with K = 10.

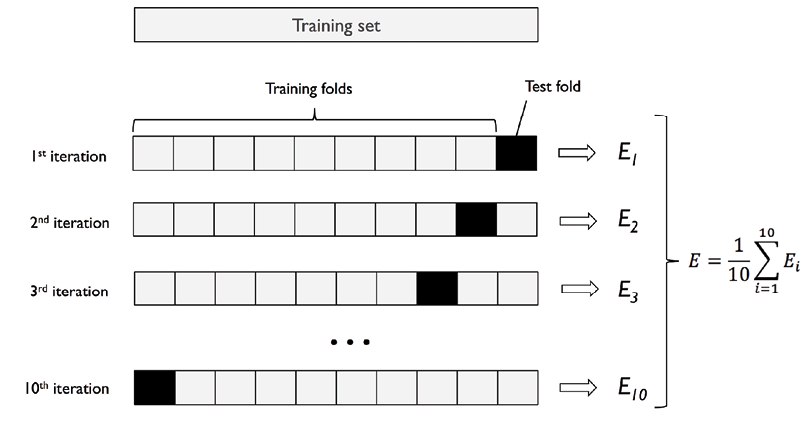
Let’s understand further with an example. For example, suppose we have a dataset of 1000 samples and we want to use k-fold cross-validation with k=5. The data set will be first split into training and test data set based on 80:20 split ratio. So, we have 800 records for training purpose. The training dataset (8000 records) would be split into 5 subsets of 160 samples each. We would then train the model on 4 of these subsets (160 samples) and evaluate its performance on the remaining subset (160 samples). This process would be repeated 5 times, with each subset of 160 samples get used as the validation data exactly once. The results from these 5 evaluations would then be averaged to produce a final evaluation metric for the model. This process will be repeated for different hyperparameters. Then, the mean and standard deviation of different models are compared and a model is selected out of all models. A new model with specific hyperparameters and algorithm is trained on entire 800 records and tested on the 200 records set aside.

Why use the Cross-validation technique?

Generally speaking, k-fold cross validation technique for training the models is found to be particularly useful when there is a limited amount of data available, as it allows us to make better use of the available data for both training and testing the model. The conventional technique for training and testing the model is to split the data into two different splits which are termed training and test split. For a decent size of data, the training and test split is taken as 70:30. Here are a few challenges due to which the cross-validation technique is used:

• Challenges with training-test split: In order to train the model for optimal performance, the hyperparameters are tweaked appropriately to achieve good model performance with the test data. However, this technique results in the risk of overfitting the test set. This is because the parameters can be tweaked until the estimator performs optimally. This way, knowledge about the test set can “leak” into the model, and evaluation metrics no longer report on generalization performance.
• Challenges with training-validation-test split: In order to take care of the above issue, there are three splits that get created. They are training, validation, and test split. The model hyperparameters get tuned using a training and validation set. And, finally, the model generalization performance is determined using a test data split. However, this technique also has shortcomings. By partitioning the data into three sets, the number of samples which can be used for learning the model gets reduced. The results depend on a particular random choice for the pair of (train, validation) sets.

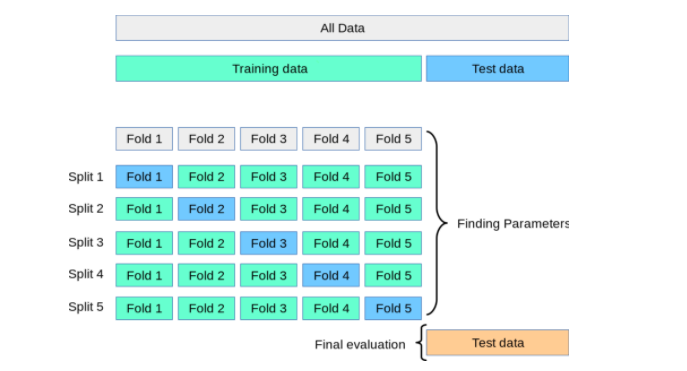
To overcome the above challenges, the cross-validation technique is used. As described earlier in this section, two different splits such as training and test split get created. However, cross-validation is applied to the training data by creating K-folds of training data in which (K-1) fold is used for training and the remaining fold is used for testing. This process is repeated for K times and the model performance is calculated for a particular set of hyperparameters by taking the mean and standard deviation of all the K models created. The hyperparameters giving the most optimal model are calculated. Finally, the model has trained again on the training data set using the most optimal hyperparameter and the generalization performance is computed by calculating model performance on the test dataset. The diagram given below represents the same.

K-fold cross-validation is also used for model selection, where it is compared against other model selection techniques such as the Akaike information criterion (AIC) and Bayesian information criterion (BIC).

To summarize, K-fold cross validation technique can be used in the following scenarios:

• Hyperparameter tuning: K-fold cross-validation can be used to tune the hyperparameters of a model. Examples of hyperparameters include the learning rate, the regularization parameter, and the number of hidden layers in a neural network. K-fold cross-validation can be used to evaluate the performance of a model on different hyperparameter settings and select the optimal hyperparameters that give the best performance.
• Model selection: K-fold cross-validation can be used to select the best model among a set of candidate models. This involves training each model on k-1 subsets of the training data and evaluating its performance on the remaining subset. The model with the best performance on the validation data is selected as the final model.
• Data preprocessing: K-fold cross-validation can also be used to evaluate the impact of different data preprocessing techniques on the performance of a model. For example, we can evaluate the performance of a model on a dataset that has been normalized using different normalization techniques.

When to select what values of K?

Here are the guidelines on when to select what value of K:

• The standard value of K is 10 and used with the data of decent size.
• For a very large data set, one can use the value of K as 5 (K-5). One can obtain an accurate estimate of the average performance of the model while reducing the computational cost of refitting and evaluating the model on the different folds.
• The number of folds increases if the data is relatively small. However, larger values of k result in an increase of the runtime of the cross-validation algorithm. This yield model performance estimates with higher variance since the training folds become smaller.
• For very small data sets, the leave-one-out cross-validation (LOOCV) technique is used. In this technique, the validation data consists of just one record.

It is recommended to use stratified k-fold cross-validation in order to achieve better bias and variance estimates, especially in cases of unequal class proportions.

K-fold Cross-Validation with Python (using Cross-Validation Generators)

In this section, you will learn about how to use cross-validation generators such as some of the following to compute the cross-validation scores. The cross-validator generators given below return the indices of training and test splits. These indices can be used to create training and test splits and train different models. Later, the mean and standard deviation of model performance of different models is computed to assess the effectiveness of hyperparameter values and further tune them appropriately.

• K-Fold: This is discussed in this past.
  
• StratifiedKFold: The StratifiedKFold cross-validation technique is a powerful tool for optimizing machine learning models. It is a way of dividing data into train and test sets while accounting for the class imbalance in the data. It works by dividing the data into k-folds, and then training the model on k-1 folds while testing it on the remaining fold. This process is repeated k times, with each fold serving as the test set once. The StratifiedKFold technique is particularly useful for imbalanced datasets, where there is a significant difference in the class proportions between train and test sets. By stratifying the folds, we can ensure that the class proportions are similar between train and test sets, which helps to avoid overfitting.
  
• GroupKFold: GroupKFold is a cross-validation technique that is commonly used in machine learning. It is similar to KFold, but instead of splitting the data into random folds, it splits the data into folds based on groups. This can be useful if there is some sort of grouping information available (e.g., time-series data). GroupKFold will first split the data into groups and then split each group into random folds. This ensures that all data points in a given fold will belong to the same group. As with KFold, GroupKFold can be used for both training and testing data. When GroupKFold is used for training data, it is important to remember that the model will only be trained on data from one group at a time. This can be beneficial if the groups are different in some way (e.g., different time periods), but it can also be a drawback if the groups are not well-separated.
  
• ShuffleSplit: The ShuffleSplit cross-validation technique is a popular method for evaluating machine learning models. The idea behind ShuffleSplit is to randomly split the data into a training set and a test set, then train the model on the training set and evaluate it on the test set. This process is repeated multiple times, and the average performance of the model is used as its final score. ShuffleSplit is particularly useful for large datasets, where it can be computationally prohibitive to run multiple train/test splits. By randomly splitting the data, ShuffleSplit ensures that every example in the dataset is given a chance to be in the training set, which helps to minimize bias.
  
• StratifiedShuffleSplit: StratifiedShuffleSplit is a variation of k-fold cross-validation that is often used when there is a need to perform multiple iterations of cross-validation, such as when the data is not i.i.d. StratifiedShuffleSplit provides train/test indices to split data into train/test sets. This cross-validation object is a merge of StratifiedKFold and ShuffleSplit, which returns stratified randomized folds. The folds are made by preserving the percentage of samples for each class. Note that StratifiedShuffleSplit should only be used for a single run of cross-validation because it will create different splits each time it is run, even if the data is unchanged.
  
• GroupShuffleSplit: In GroupShuffleSplit, the data is divided into groups and each group is shuffled separately before being split into train and test sets. This ensures that all the data is used for both training and testing and that the relationships between the features and the target are not affected by the order of the data.
  
• LeaveOneOut: LeaveOneOut cross-validation works by training the model on all but one data point, then testing it on the remaining data point. This process is repeated until each data point has been used as a test set. LeaveOneOut cross-validation is a computationally intensive method, but it provides accurate estimates of model performance. LeaveOneOut cross-validation is especially useful for small data sets, where other methods of cross-validation may not be reliable. LeaveOneOut cross-validation is also advantageous when the goal is to build a model that can be applied to new data points, as it provides an estimate of how well the model will generalize to unseen data.
  
• LeavePOut: LeavePOut cross-validation works by leaving out a portion of the data when training the model, then testing the model on the left-out data. This process is repeated multiple times, with different portions of the data being left out each time. LeavePOut cross-validation can be used with any machine learning algorithm and is a good way to get an estimate of how well a model will generalize to new data.
• LeaveOneGroupOut
• LeavePGroupsOut
• PredefinedSplit

Here is the Python code which illustrates the usage of the class StratifiedKFold (sklearn.model_selection) for creating training and test splits. The code can be found on this Kaggle page, K-fold cross-validation example. Pay attention to some of the following in the Python code given below:

• An instance of StratifiedKFold is created by passing the number of folds (n_splits=10)
• The split method is invoked on the instance of StratifiedKFold to gather the indices of training and test splits for those many folds
• Training and test data are passed to the instance of the pipeline.
• Scores of different models get calculated.
• Finally, the mean and standard deviation of model scores is computed.

from sklearn.model_selection import cross_val_score
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import StratifiedKFold
#
# Create an instance of Pipeline
#
pipeline = make_pipeline(StandardScaler(), RandomForestClassifier(n_estimators=100, max_depth=4))
#
# Create an instance of StratifiedKFold which can be used to get indices of different training and test folds
# 
strtfdKFold = StratifiedKFold(n_splits=10)
kfold = strtfdKFold.split(X_train, y_train)
scores = []
#
#
#
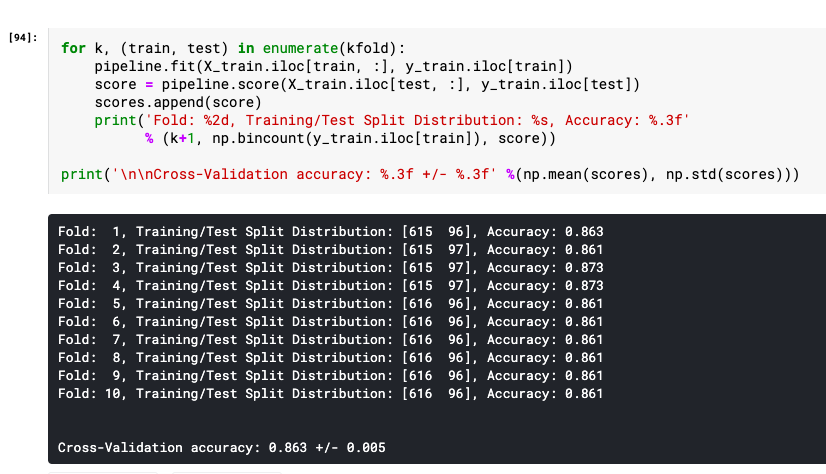
for k, (train, test) in enumerate(kfold):
    pipeline.fit(X_train.iloc[train, :], y_train.iloc[train])
    score = pipeline.score(X_train.iloc[test, :], y_train.iloc[test])
    scores.append(score)
    print('Fold: %2d, Training/Test Split Distribution: %s, Accuracy: %.3f' % (k+1, np.bincount(y_train.iloc[train]), score))

print('\n\nCross-Validation accuracy: %.3f +/- %.3f' %(np.mean(scores), np.std(scores)))

Here is what the output from the above code execution would look like:

K-fold Cross-Validation with Python (using Sklearn.cross_val_score)

Here is the Python code which can be used to apply the cross-validation technique for model tuning (hyperparameter tuning). The code can be found on this Kaggle page, K-fold cross-validation example. Pay attention to some of the following in the code given below:

• cross_val_score class of sklearn.model_selection module is used for computing the cross-validation scores. This is one of the simplest ways to It computes the scores by splitting the data repeatedly into a training and a testing set trains the estimator using the training set, and computes the scores based on the testing set for each iteration of cross-validation. The input to the cross_val_score includes an estimator (having fit and predict method), the cross-validation object, and the input dataset.
• The input estimator to the cross_val_score can be either an estimator or a pipeline (sklearn.pipeline).
• One other input to the cross_val_score is the cross-validation object which is assigned to the parameter, cv. The parameter, cv, can take one of the following values:
  • An integer that represents the number of folds in a StratifiedKFold cross validator.
  • If cv is not specified, 5-fold cross-validation is applied.
  • An instance of a cross-validation splitter can be one of the following:
    • Cross-validation generators such as some of the following:
    • Cross-validation estimators represent an estimator that has built-in cross-validation capabilities to automatically select the best hyperparameters. The following are some of the examples:
      • LogisticRegressionCV
      • ElasticNetCV

from sklearn.model_selection import cross_val_score
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
#
# Create an instance of Pipeline
#
pipeline = make_pipeline(StandardScaler(), RandomForestClassifier(n_estimators=100, max_depth=4))
#
# Pass instance of pipeline and training and test data set
# cv=10 represents the StratifiedKFold with 10 folds
#
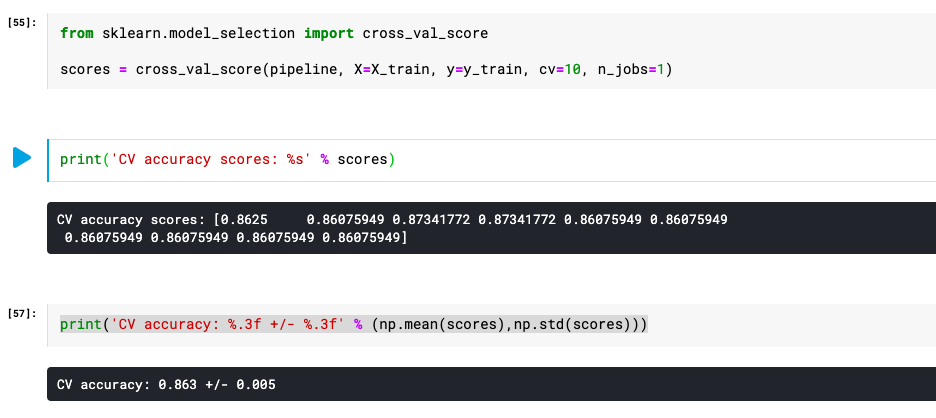
scores = cross_val_score(pipeline, X=X_train, y=y_train, cv=10, n_jobs=1)

print('Cross Validation accuracy scores: %s' % scores)

print('Cross Validation accuracy: %.3f +/- %.3f' % (np.mean(scores),np.std(scores)))

Here is how the output would look like as a result of the execution of the above code:

Disadvantages of K-fold Cross Validation

The disadvantage of k-fold cross-validation is that it can be slow to execute and it can be hard to parallelize. Additionally, k-fold cross-validation is not always the best option for all types of data sets in some of the following scenarios:

• When there is an imbalanced dataset in classification problems and there is a need to preserve the proportion of small classes, both at a target level and at the level of features. For example, fraud detection, spam detection. The solution can be stratified k-fold. In stratified k-fold cross validation, the sampling is done in a controlled way that preserves the distribution you want to preserve. You can use StratifiedKFold from Sklearn. In case of multi-label classification, one can use Scikit-multilearn package (http://scikit.ml/). Following paper can also be referred to learn about iterative stratification used in multilearn package. On the stratification of multi-label data. Machine Learning and Knowledge Discovery in Databases
• When there is an imbalanced dataset in regression problems and there is a need to preserve the distribution of a numeric variable, both at a target level and at the level of features. The solution can be stratified k-fold. One can use Pandas cut method to achieve stratification with regression problems.
• When dealing with non-independent and identically distributed (non-i.i.d) cases, such as in time series forecasting. All data points are independent and identically distributed. However, in time series data, observations are typically dependent on previous observations. This temporal dependence means that randomly splitting the data into folds (as done in k-fold cross validation) can break the temporal order, leading to training on future data and testing on past data, which is not realistic and can bias the model evaluation. The solution is to use GroupKFold from Sklearn. Another approach is to use TimeSeriesSplit from Sklearn.

Conclusions

Here is the summary of what you learned in this post about k-fold cross-validation:

• K-fold cross-validation is used for model tuning/hyperparameters tuning.
• K-fold cross-validation involves splitting the data into training and test data sets, applying K-fold cross-validation on the training data set, and selecting the model with the most optimal performance
• There are several cross-validation generators such as KFold, and StratifiedKFold which can be used for this technique.
• Sklearn.model_selection module’s cross_val_score helper class can be used for applying K-fold cross-validation in a simple manner.
• Use the LOOCV method for very small data sets.
• For very large data sets, one can use the value of K as 5.
• The value of K = 10 is standard value of K.
• It is recommended to use stratified k-fold cross-validation in order to achieve better bias and variance estimates, especially in cases of unequal class proportions.

• Author
• Recent Posts

Follow me

Ajitesh Kumar

I have been recently working in the area of Data analytics including Data Science and Machine Learning / Deep Learning. I am also passionate about different technologies including programming languages such as Java/JEE, Javascript, Python, R, Julia, etc, and technologies such as Blockchain, mobile computing, cloud-native technologies, application security, cloud computing platforms, big data, etc. For latest updates and blogs, follow us on Twitter. I would love to connect with you on Linkedin.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking. Check out my other blog, Revive-n-Thrive.com

Follow me

Latest posts by Ajitesh Kumar (see all)

• Logistic Regression in Machine Learning: Python Example - April 26, 2024
• MSE vs RMSE vs MAE vs MAPE vs R-Squared: When to Use? - April 25, 2024
• Gradient Descent in Machine Learning: Python Examples - April 22, 2024