
In this post, you will learn about the basic concepts of convolutional neural network (CNN) explained with examples. As data scientists / machine learning / deep learning enthusiasts, you must get a good understanding of convolution neural network as there are many applications of CNN.
Before getting into the details on CNN, let’s understand the meaning of Convolution in convolutional neural network.
What’s Convolution? What’s intuition behind Convolution?
Convolution represents a mathematical operation on two functions. As there can be applied different mathematical operations such as addition or multiplication on two different functions, in the similar manner, convolution operation can be applied on two different functions. Mathematically, the convolution of two different functions f and g can be represented as the following:
[latex]\Large (f*g)(x) = f(x)*g(x) = \int f(\alpha)g(x – \alpha)d\alpha[/latex]
.
Note that the symbol * DOES NOT represent multiplication. It is termed as convolution. As you say that you are multiplying the functions, with convolution, you can say you are convoluting the functions. Here is a quick introduction video on what is convolution operation on two functions f and g.
Here is a great tutorial video on understanding convolution of two functions. It demonstrates the aspect of convolution of two box function becoming a triangle when the two functions overlaps over each other. It can be noted in the video that greater the overlap between two functions, greater is the convolution.
The intuition behind convolution of f and g is the degree to which f and g overlaps when f sweeps over the function g. Here is animation representing convolution of two box functions. Note how the convolution results in a triangle when box functions overlaps with each other.
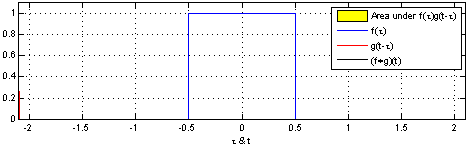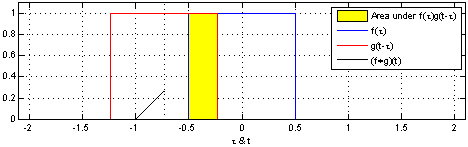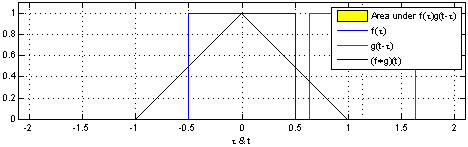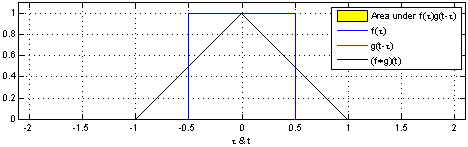
The same intuition can be taken to the convolution neural network (CNN). Convolution of two-dimensional dataset such as image can b seen as a set of convolutions sliding (or convoluting) one function (can be termed as kernel) on top of another two dimensional function (image), multiplying and adding. The convolution of image function with kernel function can result in series of image transformations (convolutions). The image given below represents the convolutions of image function with kernel function resulting in multiple data points. The kernel slides to every position of the image and computes a new pixel as a weighted sum of the pixels it floats over.
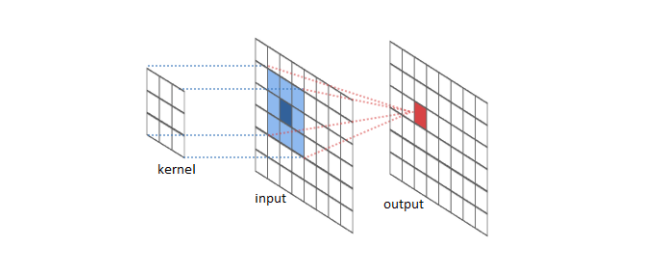
Here is another animation representing the sliding kernel function over another function and resulting in an output function (represented using output data).
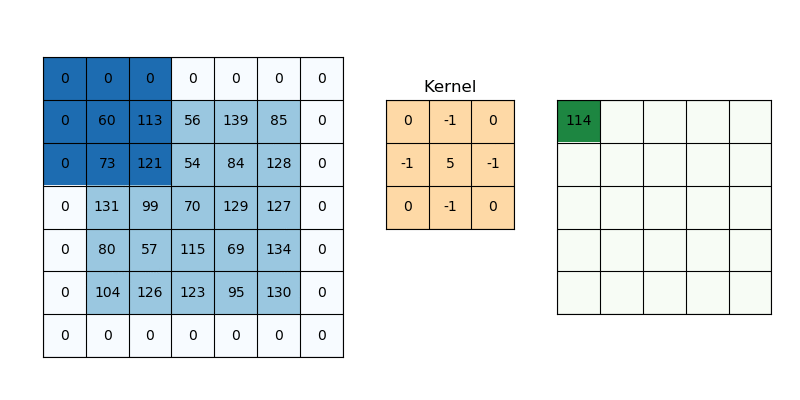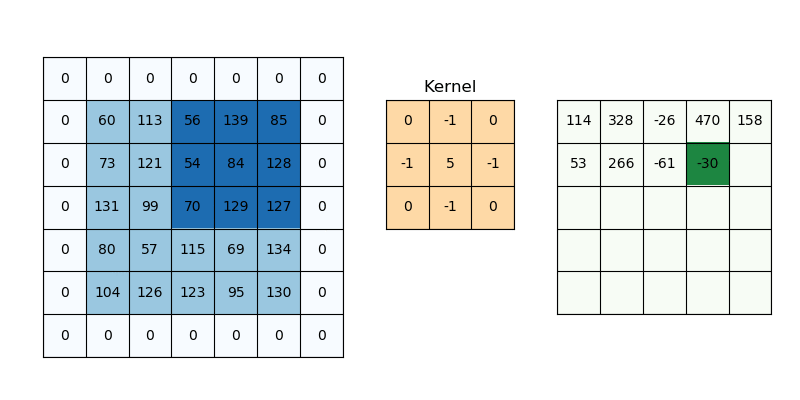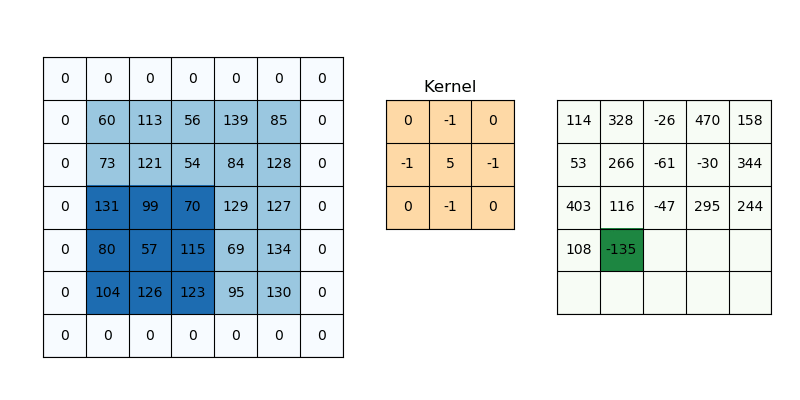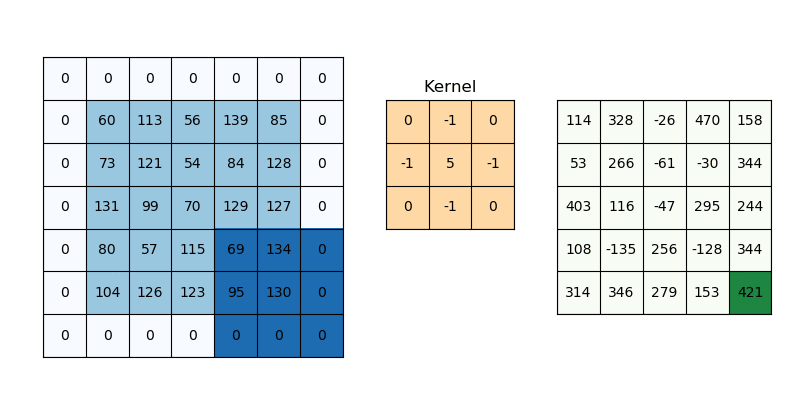
Here is a great page to understand the concepts of Convolutions – Understanding Convolutions.
What’s Convolution Neural Network (CNN)?
Convolutional neural network (CNN) is a neural network made up of the following three key layers:
- Convolution / Maxpooling layers: A set of layers termed as convolution and max pooling layer. In these layers, convolution and max pooling operations get performed.
- Fully connected layers: The convolution and max pooling layers are followed by fully connected dense layers
- Output layer: In case of classification problem, the final layer has softmax function applied to have the outcome of neural network converted into probabilities.
The diagram given below represents a simplistic CNN, used for bird image classification, having a set of convolution and max pooling layers followed by fully connected layers followed by final layer applying softmax function in order to do classification.
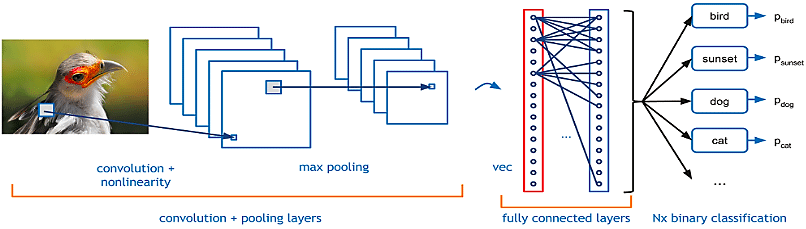
Here is a great blog on convolutional neural networks. The concept of convolution, max pooling is explained in a very nice manner.
As described in the previous section, image can be represented as a two dimensional function and the several convolution operations between the image (2-dimensional function) with another function can result in series of image transformations (convolutions). Several convolution operations between image and another function can be understood as the function sliding over different portions of image which results in the specific transformations as a result of overlap between the said function and the image. This function can be understood as a neuron. And the different portions of image can be seen as the input to this neuron. Thus, there can be large number of points pertaining to different part of images which are input to the same / identical neuron (function) and the transformation is calculated as a result of convolution. This is depicted in fig 2.
The output from neurons is passed to the max-pooling layer which consists of neurons that takes the maximum of features coming from convolution layer neurons. The output in the max pooling layer is used to determine if a feature was present in a region of the previous layer. In simple words, max-pooling layers help in zoom out.
In convolution neural network, multiple sets of convolution and max pooling layers can be configured. In the diagram below, a set of convolution layer (represented using A) and max pooling layer is shown. The output of max pooling layer is sent to another convolution layer (B). The output of convolution layer B is sent to fully connected dense layers.
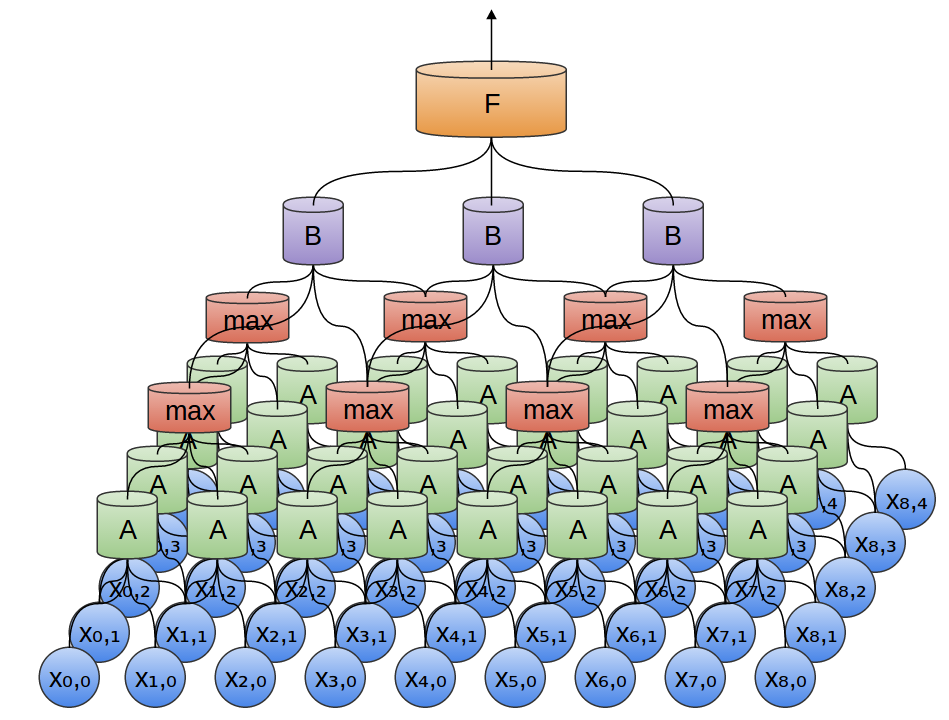
In order to train a CNN model, this is what you will need to do.
- Set of convolution and max pooling layer
- One or more fully connected dense layers
- Output layer
When training a CNN for image classification, different layers tend to learn different aspects of images such as edges, colors, texture etc.
How are Convolution layers different from Fully-connected layers?
The main difference between fully connected layers and convolution layers is that the neural network consisting of fully connected layers learn global patterns in their input feature space whereas convolution layers learn local patterns.
Let’s understand this with an example using the image of India’s prime minister, Shri Narendra Modi. The requirement is to train a model to classify whether the person in the image is Shri Narendra Modi or not. In Covid times, Shri Narendra Modi got white beard. Before Covid times, he used to be clean shaved. In case, we train the model using neural network having fully connected layers, the network trained with Narendra Modi having beard (shown below) may fail to classify the Modi’s picture having very less beard. This is because the network will learn global patterns including face features (beard etc).

If the network with fully connected layer is passed below image, it may fail to predict whether this is Narendra Modi. It would require to learn the network with fully-connected layers anew because the patterns in the below image is very different. This is because the network with fully connected layers tend to learn face features with respect to other features in the image, e.g., global patterns.

The need is to have neural network learn local patterns including face edges, face features edges, skin colors texture etc such that given any image which has lot of beard or less beard, the neural network can predict the picture as Modi’s picture with very high confidence. Technically speaking, neural network need to be translation invariant. Also, there is a need to have individual layers need individual aspects of face such as edges, colors etc which is also termed as learning spatial hierarchies of patterns.
Conclusions
Here is the summary of what you learned in relation to convolution neural network:
- Convolution neural network can be used in case of machine learning problems where data can be represented using layers. For example, image classification, NLP (words, phrases, sentences)
- Convolution neural network requires a set of convolution and max pooling layer to be trained along with the fully connected dense layer.
- Convolution operation between two functions f and g can be represented as f(x)*g(x). The * does not represent the multiplication
- Convolution operation intuitively can be thought of as a kernel function sliding over the another function thereby resulting in data which can be represented as yet another new function.
- In CNN, the sliding function (kernel) mentioned in the previous point can be understood as identical neurons or set of neurons which are passed different inputs. The output of these neurons are passed to max-pooling layer consisting of neurons which selects the maximum of feature fed as input.
- Mathematics Topics for Machine Learning Beginners - July 6, 2025
- Questions to Ask When Thinking Like a Product Leader - July 3, 2025
- Three Approaches to Creating AI Agents: Code Examples - June 27, 2025
I found it very helpful. However the differences are not too understandable for me