The central limit theorem is one of the most important concepts in statistics. This theorem states that, given a large enough sample size, the distribution of sample averages will be approximately normal. This is a huge deal because it means that we can use the normal distribution to make predictions about populations based on samples. In this article, we’ll explore the central limit theorem in more detail and look at some examples of how it works. As data scientists, it is important to understand the central limit theorem so that we can apply it to real-world situations.
What is the central limit theorem and why is it important?
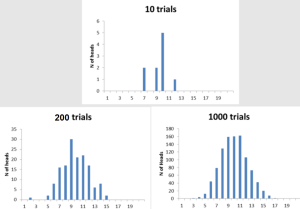
The central limit theorem is a theorem that helps to explain the behavior of a population’s average when samples are taken from it. The central limit theorem states that the distribution of the sample averages will be approximately normal, no matter what the population distribution is. Be the data in the uniform distribution or the exponential distribution or any other distribution, when many samples of these data are taken, their means get calculated and a histogram of their means is drawn, the histogram represents the normal distribution. For example, the following figure represents the original data distribution as an exponential distribution while the histogram of their means from a large number of samples comes out to be a normal distribution.
This is important because it allows us to use standard statistical techniques to analyze data even if the population distribution is not normal. One example of the central limit theorem in action is the distribution of heights of people in a population. When we take samples of heights from this population, the distribution of the sample averages will be approximately normal, even if the population distribution is not normal.
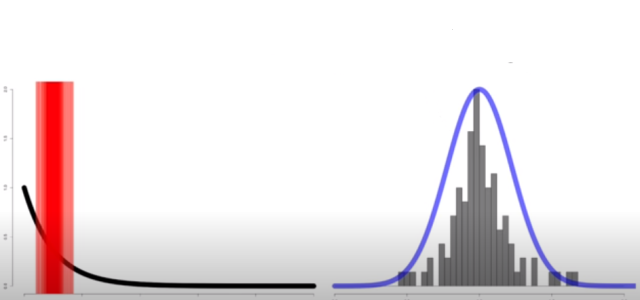
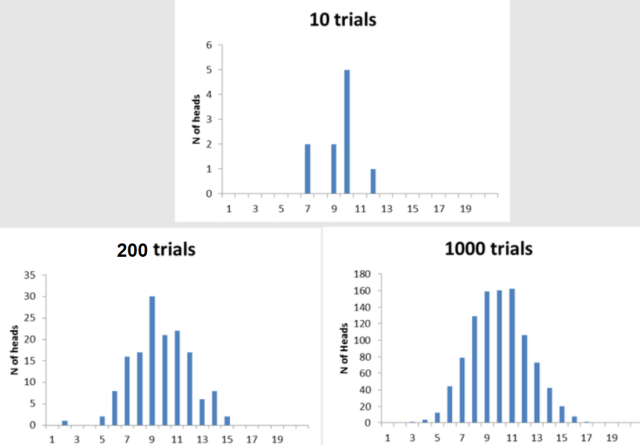
Let’s understand the central limit theorem with an experiment of a coin flipped 20 times and random variable be several times head shows up in 20 flips. The expected value will be 10 heads in 20 coin flips assuming the coin is fair. Let’s perform experiments comprising of 10, 200, and 1000 trials of flipping the coin 20 times and record the no. of times the head appeared in these different experiments. The picture below represents the distribution of X: No. of heads appearing in 20 coin flips becoming a normal distribution when the no. of trials becomes as large as 1000.
The central limit theorem is important because it helps us to understand the behavior of a population’s average when samples are taken from it. It allows us to use standard statistical techniques to analyze data even if the population distribution is not normal. This makes it easier to conclude about populations from data samples.
One common application of the central limit theorem is to use it to approximate probabilities. For example, if you want to know the probability of getting at least five heads out of ten coin flips, you can use the central limit theorem to approximate that probability. In general, if you want to know the probability of getting a certain number of successes out of a certain number of trials, you can use the central limit theorem to approximate that probability.
Another real-world application of the central limit theorem is in sampling. When we sample from a population, we typically want our sample to be representative of the population. That is, we want our sample to be as close as possible to the population as a whole. The central limit theorem can help us achieve this goal by helping us to generate samples that are more likely to be representative.
What are the advantages/benefits of the central limit theorem?
The following represents different advantages of the central limit theorem:
- Perform different statistical tests such as t-test, ANOVA, etc on data coming from any distribution, calculating confidence intervals
- Making predictions about the population
Perform statistical tests with means irrespective of data distribution
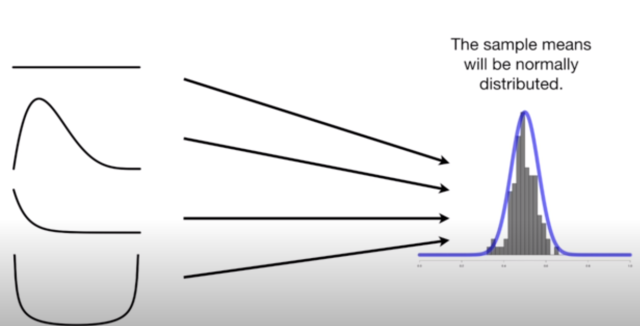
One of the greatest advantages of the central limit theorem is that it allows us to perform statistical tests with means irrespective of data distribution. This means that we can use the central limit theorem to calculate confidence intervals and test hypotheses, even if the data doesn’t follow a normal distribution. One does not need to worry about the distribution that the samples come from. This makes the central limit theorem a very versatile tool for statisticians. The picture below represents the aspect of means of data in normal distribution when data distribution belongs to different classes of distributions. The assumption is that one should be able to calculate the means of the samples.
Making predictions about the population
When we use the central limit theorem to make predictions about a population, we are making assumptions about the population. Specifically, we are assuming that the population is normally distributed. This allows us to use standard statistical techniques to make predictions about the population. For example, if we want to know the average height of people in a population, we can use the central limit theorem to predict what that average might be. We can also use the central limit theorem to predict the percentage of people in a population who will have a certain height or who will fall within a certain height range.
While the central limit theorem can be used to make predictions about populations, it is important to note that these predictions are not always accurate. In particular, the central limit theorem tends to be less accurate when the population is not normal. Therefore, it is always important to take into account the distribution of the data when making predictions about populations.
Conclusion
The central limit theorem is a very important tool for statisticians. It allows us to perform statistical tests with means irrespective of data distribution, making it a very versatile tool. Additionally, the central limit theorem helps us to make predictions about populations, even if the population is not normal. While the central limit theorem can be inaccurate when the population is not normal, it is still an incredibly useful tool. Thanks for reading!
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me