Last updated: 4th Jan, 2024
In the realm of machine learning, the emphasis increasingly shifts towards solving real-world problems with high-quality models. Creating high performant models does not not just depend on raw computational power or theoretical knowledge, but crucially on the ability to systematically conduct and learn from a myriad of different models by trying with hypothesis and related experiments including different algorithms, datasets / features, hyperparameters, etc. This is where the importance of a robust validation strategy and related techniques becomes paramount.
Validation techniques, in essence, are the methodologies employed to accurately assess a model’s errors and to gauge how its performance fluctuates with different experiments. The primary goal for the high quality model is to generalize well to unseen data, and this is where a good validation strategy truly shines. A good validation strategy is not just about improving current model performance but also about anticipating how models will perform on new, unseen data. A well-thought-out validation approach helps in making informed decisions about which models to trust.
In this post, you will briefly learn about different validation techniques such as following and also presented with practice test having questions and answers which could be used for interviews.
- Resubstitution
- Hold-out
- K-fold cross-validation
- LOOCV
- Random subsampling
- Bootstrapping
Validation Techniques for Machine Learning Models
The following are different validation techniques which can be used during training of machine learning models:
- Resubstitution: The resubstitution validation technique involves using the entire dataset for training the model. In this approach, the model’s performance is evaluated by comparing the predicted outcomes with the actual values from the same training dataset. This comparison yields the resubstitution error rate, which indicates how well the model predicts the data it was trained on. This method assesses the model’s accuracy directly on the data used for training, without utilizing a separate test set.
- Hold-out method: The hold-out validation technique is employed to mitigate the resubstitution error encountered in models trained and tested on the same dataset. In this method, the data is divided into two distinct sets: one for training and the other for testing. Common splits include 60-40, 70-30, or 80-20, with the larger portion usually dedicated to training. However, a potential issue with this approach is the uneven distribution of different classes in the training and test datasets. To address this, a process called stratification is used, ensuring that both the training and test sets have an equal representation of the various classes. This balanced distribution helps in evaluating the model’s performance more accurately and fairly across different classes. Here is a related post on this topic: Hold-out method for training machine learning models.
In Python, this can be implemented using libraries like scikit-learn. First, the dataset is divided into two sets: a training set and a testing set. This is often done using the train_test_split function from scikit-learn, where you can specify the proportion of data to be used for testing. The model is then trained on the training set using its fit method. After training, the model’s performance is evaluated on the unseen testing set using different types of metrics.
- K-fold cross-validation: K-fold cross-validation is a robust and widely-used method for assessing the performance of machine learning models. In this technique, the dataset is partitioned into ‘k’ equal-sized subsets or ‘folds’. The model is then trained and validated ‘k’ times, with each of the ‘k’ folds used exactly once as the validation set, while the remaining ‘k-1’ folds are used for training. This process results in ‘k’ different performance scores, which are typically averaged to produce a single estimation. The key advantage of k-fold cross-validation is its ability to utilize all available data for both training and validation, providing a comprehensive evaluation of the model’s performance. This can also be termed as probabilistic approach. It does rely on data sampling strategy, or the manner in which different set of data is sampled for training the models.
In scikit-learn, the K-fold cross-validation process is facilitated by the KFold class from the model_selection module. This class allows you to specify the number of splits (folds) you want to use. To actually perform the cross-validation, you typically use the cross_val_score function, also from the model_selection module, which takes your model, the entire dataset, and the number of folds as arguments, and returns the evaluation scores for each fold.
Figure 1. K-fold cross-validation
This validation method is particularly useful for smaller datasets where maximizing the use of data is crucial. By averaging over ‘k’ trials, k-fold cross-validation also helps in reducing the variability of the performance estimation compared to a single train-test split, leading to a more reliable assessment of the model’s effectiveness. This technique can also be called as a form of Repeated Hold-out Method. The error rate could be improved by using stratification technique. Here is a related post: K-fold cross validation method for machine learning models.
- Leave-one-out cross-validation (LOOCV): In LOOCV, the validation method is carried out as many times as there are data points in the dataset. Specifically, for a dataset with ‘N’ instances, the model undergoes ‘N’ training and validation cycles. In each cycle, the model is trained on all data points except one, which is held out for testing. This means that in each iteration, the model is trained on ‘N-1’ data points and validated on the single excluded data point. The primary advantage of LOOCV is its ability to use nearly all the data for training, which can be particularly beneficial in scenarios where the dataset is limited in size.
LOOCV method, however, can be computationally intensive, especially for large datasets, as it requires the model to be trained from scratch ‘N’ times. Despite this, the results from LOOCV tend to be less biased and more reliable, especially in cases where every data point’s contribution to the model’s learning is crucial. The following diagram represents the LOOCV validation technique.
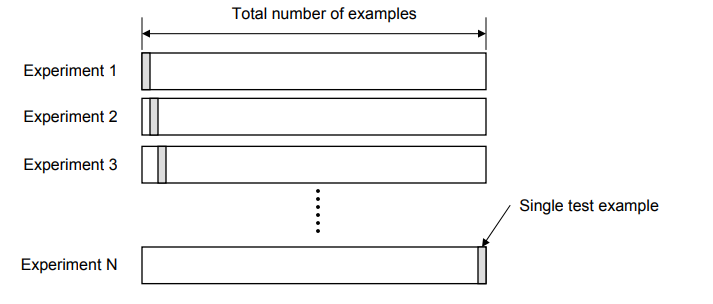
Figure 2. LOOCV validation technique
- Random Subsampling is a validation technique characterized by its approach of randomly selecting multiple subsets of data from the dataset to form distinct test datasets. For each of these subsets, the remaining data points in the dataset are used to create the corresponding training dataset. This method involves running several iterations, with each iteration having a different random split between training and testing data.
The process can be visualized as a cycle where, in each iteration, a new random sample is chosen as the test set, and the model is trained and evaluated on these varying splits. After conducting a predefined number of iterations, the error rates from each iteration are calculated and then averaged to provide an overall error rate for the model.
This averaging is a critical aspect of random subsampling, as it helps in mitigating the impact of any particularly biased or unrepresentative split of the data. By repeatedly shuffling and splitting the dataset, random subsampling offers a more robust estimate of the model’s performance compared to a single split, as it accounts for variability in the dataset. However, it’s important to note that since this method involves multiple rounds of training and validation, it can be computationally more intensive than a single train-test split, especially for larger datasets. Despite this, random subsampling remains a popular choice for model validation due to its simplicity and effectiveness in providing a reliable performance estimate.
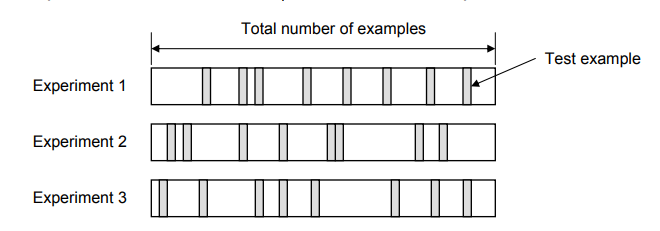
Figure 3. Random Subsampling validation technique
- Bootstrapping: In this technique, the training data set is randomly selected with replacement. The remaining examples that were not selected for training are used for testing. Unlike K-fold cross-validation, the value is likely to change from fold-to-fold. The error rate of the model is average of the error rate of each iteration. The following diagram represents the same.
Figure 4. Bootstrapping validation technique
Practice Test – ML Model Validation Techniques
[wp_quiz id=”6694″]
Further Reading / References
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me