Ever found yourself wondering why your deep learning (deep neural network) model is simply refusing to learn? Or struggled to comprehend why your deep neural network isn’t reaching the accuracy you expected? The culprit behind these issues might very well be the infamous vanishing gradient problem, a common hurdle in the field of deep learning.
Understanding and mitigating the vanishing gradient problem is a must-have skill in any data scientist‘s arsenal. This is due to the profound impact it can have on the training and performance of deep neural networks. In this blog post, we will delve into the heart of this issue, learning the calculus behind neural networks and exploring the role of activation functions in the emergence of vanishing gradients. We’ll also learn about how to detect this problem during model training and use a set of practical tools and techniques to overcome it.
What’s Vanishing Gradient Problem in Deep Learning?
Even before we start learning about the concepts of vanishing gradient, let’s quickly take a look at what is gradient and gradient descent.
The gradient is a vector that points in the direction of the greatest rate of increase of a function, and its magnitude is the rate of increase in that direction. In machine learning, specifically deep learning, the function we’re interested in is the loss function, and our goal is to find the model parameters that minimize the loss. We do this by initializing the parameters to some random values, computing the gradient of the loss with respect to the parameters, and then adjusting the parameters in the direction of the negative gradient (i.e., the direction of the steepest descent). This process is known as gradient descent.
When working with deep learning models (neural networks), the backpropagation method is used to compute these gradients. It involves applying the chain rule of calculus to compute the derivative of the loss function with respect to each parameter. In deep neural networks, this involves computing gradients for each layer, starting from the output layer and working backward through the network.
Now that we understood the concept of gradient, gradient descent, and backpropagation method in deep learning models, let’s understand the concept of vanishing gradient.
The vanishing gradient problem arises specifically for deep neural networks. As we backpropagate through the network, we’re essentially multiplying a series of gradients together. If these gradients are small (less than 1), then the product of many such small numbers can become vanishingly small—i.e., close to zero. What this means in practice is that the parameters in the early layers of the network (closer to the input) receive very little update, because their gradients are so small. This can significantly slow down the training process, because these early layers may not learn effectively. It can also lead to the model getting stuck in poor solutions because the small gradients provide very little information on how to improve the parameters.
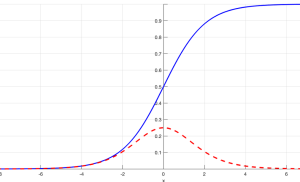
The vanishing gradient problem is especially pronounced in networks with sigmoid or hyperbolic tangent (tanh) activation functions because the gradients of these functions can be very small. For instance, the derivative of the sigmoid function is at most 0.25, and for inputs with large absolute values, it’s nearly 0. In a deep network with many layers, this can lead to vanishingly small gradients.
How do we know that there is a vanishing gradient problem?
Detecting the vanishing gradient problem can be a bit tricky, but here are some common indicators that may suggest your model is experiencing this issue:
- Slow Training or Non-improving Training Loss: The most common symptom is that training is very slow or the training loss stops decreasing after a certain number of epochs. This happens because the weights in the early layers of the network aren’t being updated effectively due to the small gradients.
- Poor Performance on Training Data: The model underperforms or shows high bias even on the training data. This happens because the early layers of the network, which are crucial for capturing low-level features, fail to learn effectively.
- Checking the Magnitude of Gradients: You can programmatically inspect the gradients during training. If the gradients of the earlier layers are several orders of magnitude smaller than the gradients of the later layers, it’s an indication of the vanishing gradient problem. In some deep learning frameworks like TensorFlow or PyTorch, you can access and monitor these gradients.
- Unresponsive Neurons in Early Layers: If neurons in early layers have almost the same output for different inputs, or their outputs don’t change much during training, that could be a sign that those neurons aren’t learning effectively due to the vanishing gradient problem.
- Reliance on Upper Layers: If your model’s performance doesn’t suffer much when you remove or randomize the early layers, that could be a sign that those layers aren’t doing much learning and are suffering from the vanishing gradient problem.
Solutions to Vanishing Gradient Problem
The following are some of the solutions proposed for the vanishing gradient problem:
- Weight Initialization: Techniques like Glorot or Xavier initialization help to set the initial weights to prevent early saturation of activation functions, reducing the chances of vanishing/exploding gradients.
- Non-saturating Activation Functions: ReLU and its variants (Leaky ReLU, Parametric ReLU, etc.) are less susceptible to the vanishing gradient problem because their gradients are either 0 (for negative inputs) or 1 (for positive inputs).
- Batch Normalization: This technique normalizes layer inputs to have zero mean and unit variance, which can help to alleviate the vanishing gradient problem.
- Residual Connections (Skip Connections): Used in ResNet architecture, these allow gradients to propagate directly through several layers by having identity shortcuts from early layers to later layers.
- Gradient Clipping: This technique is used to prevent exploding gradients but can sometimes mitigate vanishing gradients as well by bounding the overall gradient value.
- Using LSTM/GRU in Recurrent Neural Networks (RNNs): LSTM and GRU have gating mechanisms that can manage the gradient flow and tackle the vanishing gradient problem in the context of RNNs.
Conclusion
The vanishing gradient problem is a challenging pitfall in the world of deep learning, where gradients reduce to minuscule sizes, slowing down training and hindering model performance. It arises due to the multiplication of small gradients, particularly in deep networks and with certain activation functions, leading to almost non-existent weight updates in earlier layers.
Detecting the vanishing gradient problem may involve observing slow or non-improving training losses, monitoring the magnitudes of gradients, or noticing unresponsive neurons in the initial layers. Luckily, the problem isn’t insurmountable. Solutions range from using appropriate activation functions and proper weight initialization techniques to applying batch normalization or altering the network architecture. With these tools in hand, the challenge of vanishing gradients can be effectively addressed, paving the way for successful deep-learning applications.
- The Watermelon Effect: When Green Metrics Lie - January 25, 2026
- Coefficient of Variation in Regression Modelling: Example - November 9, 2025
- Chunking Strategies for RAG with Examples - November 2, 2025

I found it very helpful. However the differences are not too understandable for me