You may have heard of Linear Discriminant Analysis (LDA), but you’re not sure what it is or how it works. In the world of machine learning, Linear Discriminant Analysis (LDA) is a powerful algorithm that can be used to determine the best separation between two or more classes. With LDA, you can quickly and easily identify which class a particular data point belongs to. This makes LDA a key tool for solving classification problems.
In this blog post, we will discuss the key concepts behind LDA and provide some examples of how it can be used in the real world!
What is Linear Discriminant Analysis (LDA) and what are its key benefits?
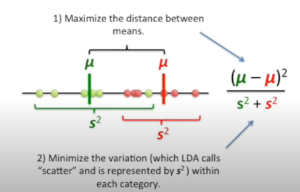
Linear Discriminant Analysis, or LDA, is a machine learning algorithm that is used to find the Linear Discriminant function that best classifies or discriminates or separates two classes of data points. LDA is a supervised learning algorithm, which means that it requires a labelled training set of data points in order to learn the Linear Discriminant function. Once the Linear Discriminant function has been learned, it can then be used to predict the class label of new data points. LDA is similar to PCA (principal component analysis) in the sense that LDA reduces the dimensions. However, the main purpose of LDA is to find the line (or plane) that best separates data points belonging to different classes. The key idea behind LDA is that the decision boundary should be chosen such that it maximizes the distance between the means of the two classes while simultaneously minimizing the variance within each classes data or within-class scatter. This criterion is known as the Fisher criterion and can be expressed as the following formula for two classes:
In the above picture, data get projected on most appropriate separating line or hyperplane such that the distance between the means is maximized and the variance within the data from same class is minimized.
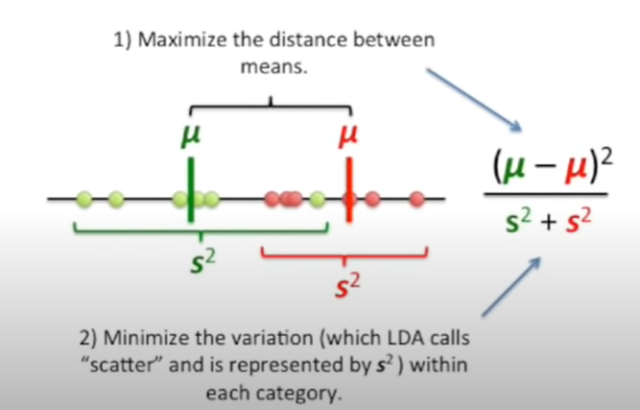
LDA works by projecting the data onto a lower-dimensional space while preserving as much of the class information as possible and then finding the hyperplane that maximizes the separation between the classes based on Fisher criterian. The picture below represents aspect of projecting the data on a separation line and finding the best possible line. Learn more about it in the StatQuest video on LDA (pictures taken from the video)
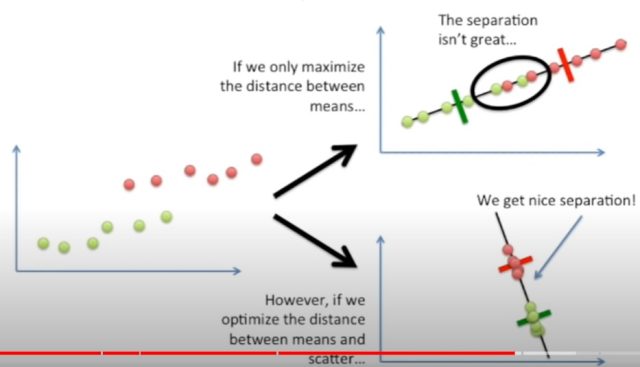
The aspect of finding the best separation line makes LDA particularly well-suited for classification tasks. In addition, LDA is not susceptible to the “curse of dimensionality” like many other machine learning algorithms, meaning that it can be used with data sets that have a large number of features. The picture below represents the aspect of finding the line that best separates the data points based on the Fisher criterian.
Although LDA is a powerful tool for classification, it is worth noting that it makes some strong assumptions about the data. In particular, LDA assumes that the data points in each class are drawn from a Gaussian distribution. Violation of this assumption can lead to poor performance of LDA on real data sets. This assumption is important because it means that the groups can be considered to be independent of each other. The normal distribution assumption means that LDA is scale-invariant, meaning that it is not affected by changes in units of measurement. This makes LDA particularly well-suited for applications where data from different sources needs to be compared, such as facial recognition.
The following are some of the benefits of using LDA:
- LDA is used for classification problems.
- LDA is a powerful tool for dimensionality reduction.
- LDA is not susceptible to the “curse of dimensionality” like many other machine learning algorithms.
How LDA works and the steps involved in the process?
LDA is a supervised machine learning algorithm that can be used for both classification and dimensionality reduction. LDA algorithm works based on the following steps:
- The first step is to calculate the means and standard deviation of each feature.
- Within class scatter matrix and between class scatter matrix is calculated
- These matrices are then used to calculate the eigenvectors and eigenvalues.
- LDA chooses the k eigenvectors with the largest eigenvalues to form a transformation matrix.
- LDA uses this transformation matrix to transform the data into a new space with k dimensions.
- Once the transformation matrix transforms the data into new space with k dimensions, LDA can then be used for classification or dimensionality reduction
Examples of how LDA can be used in practice
The following are some examples of how LDA can be used in practice:
- LDA can be used for classification, such as classifying emails as spam or not spam.
- LDA can be used for dimensionality reduction, such as reducing the number of features in a dataset.
- LDA can be used to find the most important features in a dataset.
Conclusion
Linear discriminant analysis (LDA) is a powerful machine learning algorithm that can be used for both classification and dimensionality reduction. LDA is particularly well-suited for tasks such as facial recognition where data from different sources needs to be compared. LDA makes some strong assumptions about the data, in particular that the data points are drawn from a Gaussian distribution. However, LDA is still one of the most widely used machine learning algorithms due to its accuracy and flexibility. LDA can be used for a variety of tasks such as classification, dimensionality reduction, and feature selection. With its many applications, LDA is a machine learning algorithm that is worth learning. Thanks for reading!
I hope you enjoyed this post on Linear Discriminant Analysis (LDA). If you have any questions, please feel free to leave a comment below. I will try my best to answer your questions. Thanks for reading!
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.
- Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
- LLMs for Adaptive Learning & Personalized Education - October 8, 2024
- Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024
I found it very helpful. However the differences are not too understandable for me